3.4 直线与圆的位置关系 教案(表格式) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 3.4 直线与圆的位置关系 教案(表格式) 2025-2026学年数学青岛版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 367.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:40:12 | ||
图片预览



文档简介
3.4 直线与圆的位置关系
课题 3.4 直线与圆的位置关系 课时 第1课时 授课人
教学目标 1.经历探索直线与圆的位置关系的过程. 2.通过观察得出“圆心到直线的距离d和半径r的数量关系”与“直线和圆的位置关系”,能进行位置关系与数量关系的相互转化.
教学 重难点 教学重点:直线与圆的位置关系. 教学难点:直线与圆的位置关系的判断方法.
教学活动
教学流程 师生活动 设计意图
课前小测 1.圆周角定理内容是什么 圆周角等于它所对弧上的圆心角的一半. 2.它的推论有哪些 推论1 圆周角的度数等于它所对弧的度数的一半. 推论2 同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等. 推论3 直径所对的圆周角是直角;90°的圆周角所对的弦是直径. 推论4 圆内接四边形的对角互补. 复习之前所学,加以巩固.
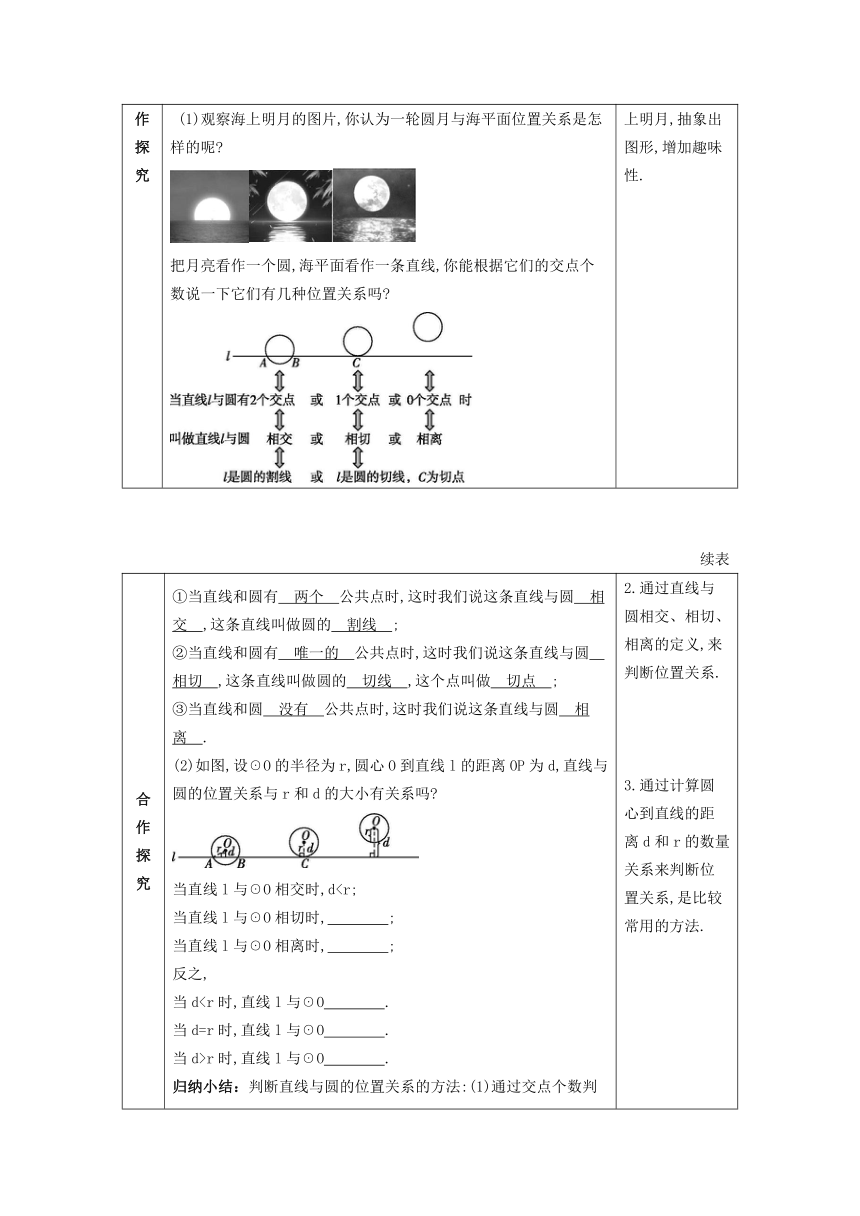
情境导入 问题一:在平面内一个点P与☉O的位置关系有几种 有三种.点在圆外;点在圆上;点在圆内. 问题二:已知☉O的半径为r,通过怎样的数量关系可以确定点P与☉O的位置关系 连接OP: (1)当OP>r时,点P在圆外; (2)当OP合作探究 探究:直线与圆的位置关系 (1)观察海上明月的图片,你认为一轮圆月与海平面位置关系是怎样的呢 把月亮看作一个圆,海平面看作一条直线,你能根据它们的交点个数说一下它们有几种位置关系吗 1.借助美丽的海上明月,抽象出图形,增加趣味性.
续表
合作探究 ①当直线和圆有 两个 公共点时,这时我们说这条直线与圆 相交 ,这条直线叫做圆的 割线 ; ②当直线和圆有 唯一的 公共点时,这时我们说这条直线与圆 相切 ,这条直线叫做圆的 切线 ,这个点叫做 切点 ; ③当直线和圆 没有 公共点时,这时我们说这条直线与圆 相离 . (2)如图,设☉O的半径为r,圆心O到直线l的距离OP为d,直线与圆的位置关系与r和d的大小有关系吗 当直线l与☉O相交时,dr时,直线l与☉O . 归纳小结:判断直线与圆的位置关系的方法:(1)通过交点个数判断; (2)根据圆心到直线的距离与半径的大小关系判断. 典例分析: 【例】 在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm.以点C为圆心,r为半径画圆.当r分别取下列各值时,斜边AB所在的直线与☉C具有怎样的位置关系 (1)r=2 cm;(2)r=2.4 cm;(3)r=3 cm. 解:如图,经过点C作CD⊥AB,垂足为点D. 在Rt△ABC中,由勾股定理,得 AB===5. ∵Rt△ADC∽Rt△ACB,∴=. ∴CD===2.4, 即圆心C到AB的距离d=2.4 cm. (1)当r=2 cm时,d>r,直线AB与☉C相离; (2)当r=2.4 cm时,d=r,直线AB与☉C相切; (3)当r=3 cm时,d随堂检测 1.若直线l和☉O有公共点,则直线l与☉O( D ) A.相离 B.相切 C.相交 D.相切或相交 2.已知圆的半径为4 cm,若直线上一点与圆心距离为6 cm,则直线与圆的位置关系是( D ) A.相离 B.相切 C.相交 D.无法确定
续表
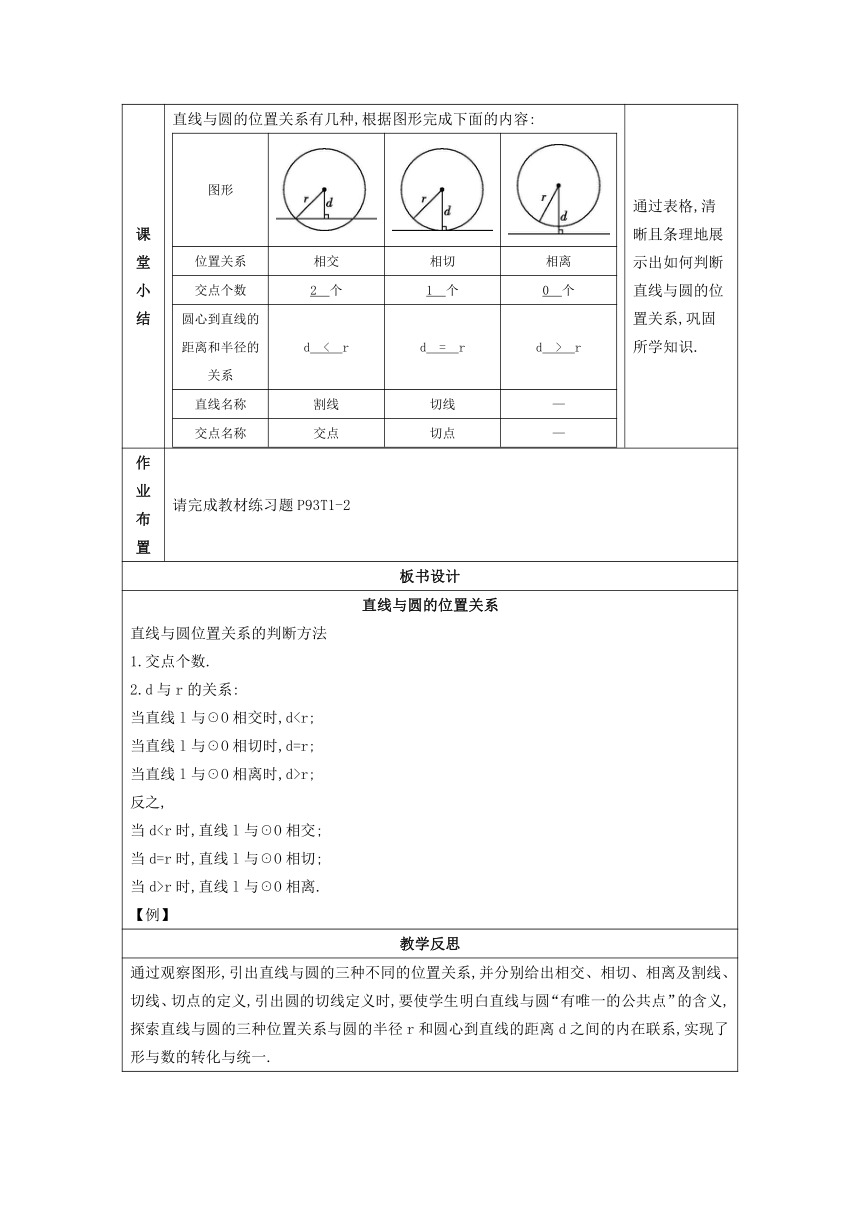
随堂检测 3.已知☉O的半径为7,圆心O到直线AB的距离为d,根据条件填写d的范围: 若AB和☉O相离,则 d>7 ;若AB和☉O相切,则 d=7 ;若AB和☉O相交,则 d<7 . 4.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的取值情况是 3课堂小结 直线与圆的位置关系有几种,根据图形完成下面的内容: 图形位置关系相交相切相离交点个数2 个1 个0 个圆心到直线的距离和半径的关系d < rd = rd > r直线名称割线切线—交点名称交点切点—
通过表格,清晰且条理地展示出如何判断直线与圆的位置关系,巩固所学知识.
作业布置 请完成教材练习题P93T1-2
板书设计
直线与圆的位置关系 直线与圆位置关系的判断方法 1.交点个数. 2.d与r的关系: 当直线l与☉O相交时,dr; 反之, 当dr时,直线l与☉O相离. 【例】
教学反思
通过观察图形,引出直线与圆的三种不同的位置关系,并分别给出相交、相切、相离及割线、切线、切点的定义,引出圆的切线定义时,要使学生明白直线与圆“有唯一的公共点”的含义,探索直线与圆的三种位置关系与圆的半径r和圆心到直线的距离d之间的内在联系,实现了形与数的转化与统一.
课题 3.4 直线与圆的位置关系 课时 第2课时 授课人
教学目标 1.掌握切线的判定定理,培养学生的探索能力. 2.能运用切线的判定定理进行证明和计算.
教学重难点 教学重点:会用切线的判定定理进行证明和计算. 教学难点:选择正确的方法证明相切.
教学活动
教学流程 师生活动 设计意图
课前小测 1.直线与圆的位置关系有哪些 相交,相切,相离. 2.如何判断直线与圆的位置关系 (1)由直线与圆的交点个数判断:2个交点,相交;1个交点,相切;没有交点,相离. (2)由圆心到直线的距离d和半径r的关系判断: 当d>r时,相离;当d=r时,相切;当d情境导入 判断直线与圆相切的方法有哪些 ①当直线与圆有唯一交点时,相切; ②过圆心作直线的垂线段d,当d=r时,相切. 复习直线与圆相切的判定方法,为进一步探究相切做好准备.
合作探究 探究:切线的判定定理 问题1:过☉O的半径OA的外端点A作与半径OA垂直的直线l(如图),你发现直线l与☉O有怎样的位置关系 为什么 解:相切. 因为圆心O到直线l的距离等于☉O的半径,所以直线l与☉O相切. 归纳小结: 切线的判定定理 过半径的外端并且垂直于半径的直线是圆的切线. 注意: “过半径的外端”和“垂直于半径”这两个条件缺一不可,否则就不是圆的切线. 问题2:利用上面的定理,过☉O上任意一点,你会用三角尺画☉O的切线吗 试一试. 解:设P是☉O上的任意一点,将三角尺的直角顶点与P点重合,一条直角边过圆心O,再沿另外一条直角边画直线,该直线便是☉O的经过点P的切线. 1.问题1让学生利用尺规作图,经过一点作已知直线的垂线,让学生发现是切线,并说出理由(d=r). 2.问题2先让学生尝试画图,通过交流,得到画法.
续表
合作探究 典例分析: 【例1】 如图,以△ABC的边AB为直径作☉O,如果☉O经过AC的中点D,然后过D作DE⊥BC,垂足为点E.DE是☉O的切线吗 说明理由. 解:DE是☉O的切线.理由如下:连接OD. ∵AB是☉O的直径,∴AO=OB. 又∵AD=DC, ∴OD是△ABC的中位线,从而OD∥BC. ∵DE⊥BC,∴DE⊥OD, ∴DE是☉O的切线. 在例1中,你还能由已知探索出哪些结论 说明你的理由. 解:连接BD. ∵AB是☉O的直径,∴BD⊥AC. 又∵D是AC的中点, ∴BD是AC的垂直平分线, ∴AB=BC,∠A=∠C. 【例2】 已知O为∠BAC平分线上一点,OD⊥AB于点D,以O点为圆心,OD为半径作☉O.求证:☉O与AC相切. 证明:过点O作OE⊥AC于点E. ∵AO平分∠BAC,OD⊥AB, ∴OE=OD, 即圆心O到AC的距离d=r, ∴AC是☉O切线. 讨论:例1和例2有何不同 归纳小结: 1.当已知条件中直线与圆有交点时,连接圆心和交点就作出了半径,相当于已知直线过半径的外端,只需要证明此直线垂直于半径即可得到结论.简记为“有交点,连半径,证垂直”. 2.从已知条件中读不出直线与圆有交点时,过圆心作直线的垂线段,证明垂线段等于半径(d=r),也可得到相切.简记为“无交点,作垂直,证半径”. 3.例1是连半径,证垂直,是切线判定的基础题型,也是中考的必考题,要让学生掌握方法. 4.例2是作垂直,证半径,是学生学习的难点,要掌握方法. 5.及时归纳应用切线的判定定理的思路的不同之处,找出关键点.让学生更清楚明白.
续表
随堂检测 1. 如图,AB是☉O的直径,点D在AB的延长线上,BD=OB,点C在☉O上,∠CAB=30°.求证:DC是☉O的切线. 证明:如图,连接OC,BC. ∵AB是☉O的直径,∴∠ACB=90°. ∵∠CAB=30°,∴∠ABC=60°. ∵OB=OC,∴△OBC为等边三角形, ∴∠OBC=60°,BC=OB=BD, ∴△BCD为等腰三角形,∠CBD=120°, ∴∠BCD=30°,∴∠OCD=∠OCB+∠BCD=90°, ∴DC是☉O的切线. 2.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AC于点E,以点O为圆心,OE长为半径作☉O.求证:AB是☉O的切线. 证明:如图,过点O作OF⊥AB于点F. ∵AB=AC,AO⊥BC,∴AO是∠BAC的平分线. ∵OE⊥AC,OF⊥AB,∴OF=OE, ∴AB是☉O的切线.
课堂小结 1.切线的判定方法有几种 2.切线的判定定理的内容是什么 应用定理时,需要注意什么 3.应用切线的判定定理有几种思路 是什么 便于学生梳理知识点,使知识更清晰条理.
作业布置 请完成教材练习题P94T1-T2
板书设计
切线的判定 1.切线的判定定理:过半径的外端并且垂直于半径的直线是圆的切线. 2.应用切线的判定定理的两种思路 (1)有交点,连半径,证垂直. (2)无交点,作垂直,证半径. 【例2】
教学反思
切线的判定定理是圆中的重点,是中考必考的内容.在学习这节课时,先让学生利用尺规作图发现直线是圆的切线并说出理由,从而得到切线的判定定理,教学时应提醒学生“过半径的外端”和“垂直于半径”这两个条件缺一不可,否则就不是圆的切线.这个定理是由“当d=r时,直线l与☉O相切”推出的.例1和例2可让学生独立思考,互相交流,发现它们的不同之处,总结关键点,以免在以后的证明中出现错误.
课题 3.4 直线与圆的位置关系 课时 第3课时 授课人
教学目标 1.经历探索切线的性质的过程,培养学生的探索能力. 2.会利用切线的性质解决相关的问题.
教学 重难点 教学重点:切线的性质定理的应用. 教学难点:用反证法证明切线的性质定理.
教学活动
教学流程 师生活动 设计意图
课前小测 切线的判定方法有哪些 (1)交点个数:当直线与圆有一个交点时,相切. (2)当圆心到直线的距离d=r时,相切. (3)过半径的外端并且垂直于半径的直线是圆的切线. 复习切线的判定方法,巩固旧知.
情境导入 问题1:你能说出切线的判定定理的逆命题吗 圆的切线垂直于经过切点的半径. 问题2:这个逆命题是真命题还是假命题 让学生通过画图对它的正确性作出猜想. 由学生说出切线的判定定理的逆命题,引出本节课的课题.
合作探究 探究:切线的性质定理 如果是真命题,你能给出证明吗 不好直接证明,用反证法能行吗 已知:如图,直线l与☉O相切于点A. 求证:OA⊥l. 证明:如图,假设l与半径OA不垂直.过点O作OB⊥直线l,垂足为点B.在l上取BA'=BA,且使B点在A与A'之间,连接OA'. 于是OB垂直平分AA',OA=OA'. ∵点A是切点,OA是☉O的半径, ∴OA'也是☉O的半径. 这就是说,直线l与☉O有两个公共点,即l与☉O相交,这与已知条件“直线l与☉O相切于点A”矛盾,所以OA⊥l. 归纳小结:切线的性质定理 圆的切线垂直于经过切点的半径. 几何语言:如图,l是☉O的切线,A为切点. ∵l是☉O的切线,A为切点, ∴OA⊥l. 切线的其他性质: (1)切线与圆只有一个交点; (2)圆心到切线的距离等于圆的半径. 1.引导学生尝试证明,当发现用直接证明不好解决时,尝试用反证法证明.
续表
合作探究 典例分析: 【例1】 已知A,B,C是☉O上的三点,经过点A,点B分别作☉O的切线,两切线相交于点P,如果∠P=42°,求∠ACB的度数. 解:(1)如图①,当点C在上时,连接OA,OB. ∵PA,PB是☉O的切线,A,B是切点, ∴∠OAP=∠OBP=90°. 在四边形OAPB中,∵∠P=42°, ∴∠AOB=360°-∠OAP-∠OBP-∠P=360°-90°-90°-42°=138°, ∴∠ACB=∠AOB=×138°=69°. (2)如图②,当点C在劣弧上时,在优弧上任取一点C',连接AC',BC'. 由(1)知,∠AC'B=69°. 在圆内接四边形ACBC'中, ∵∠ACB+∠AC'B=180°, ∴∠ACB=180°-∠AC'B=180°-69°=111°. ① ② 【例2】 如图,△ABC内接于☉O,AB是☉O的直径,点D在☉O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.求证:DC=BC. 证明:如图,连接OC. ∵CE是☉O的切线,∴OC⊥CE. ∵AE⊥CE,∴OC∥AE,∴∠OCA=∠EAC. ∵OC=OA,∴∠OCA=∠OAC,∴∠EAC=OAC, ∴=,∴DC=BC. 你还有其他的方法吗 2.例1是一题多解题,是易错题,易考题,要考虑周全. 3.例2采用不同的方法来完成证明,第二个方法侧重于垂径定理的推论“知二推三”的应用.
随堂检测 1.如图,AB是☉O的弦,AC是☉O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( D ) A.20° B.25° C.40° D.50° 2.如图,☉M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是 (5,4) .
续表
随堂检测 3.如图,在△ABC中,BC是以AB为直径的☉O的切线,且☉O与AC相交于点D,E为BC的中点,连接DE.求证:DE是☉O的切线. 证明:如图,连接OD,BD. ∵OD=OB,∴∠ODB=∠OBD. ∵AB是☉O的直径, ∴∠ADB=90°, ∴∠CDB=90°. ∵E为BC的中点, ∴DE=BE, ∴∠EDB=∠EBD, ∴∠ODB+∠EDB=∠OBD+∠EBD, 即∠EDO=∠EBO. ∵BC是以AB为直径的☉O的切线, ∴AB⊥BC,∴∠EBO=90°, ∴∠ODE=90°, ∴DE是☉O的切线.
课堂小结 1.切线的性质有哪些 2.在已知圆的切线的条件下,一般怎样做 让学生熟记切线的性质定理,知切线,连半径,得垂直.
作业布置 请完成教材练习题P96T1-T2
板书设计
切线的性质 1.切线的性质定理:圆的切线垂直于经过切点的半径. 几何语言:如图,l是☉O的切线,A为切点. ∵l是☉O的切线,A为切点, ∴OA⊥l. 2.切线的其他性质 (1)切线与圆只有一个交点; (2)圆心到切线的距离等于圆的半径. 【例2】
教学反思
本节课先引导学生复习切线的判定定理,再让学生说出它的逆命题,通过画图作出猜想.在用直接证明法不好证明时,尝试用反证法进行证明,对学生来说是个难点.学生对反证法证明的思路和实质还缺乏真正的理解,因此往往停留在形式的模仿上,在讲解时,速度要慢,不断加深对这个方法的认识.例1是一题多解,点C在优弧还是劣弧上不能确定时,一定要分情况讨论.例2综合性强一些,考察切线的性质,圆周角定理的推论,垂径定理的推论的应用.
课题 3.4 直线与圆的位置关系 课时 第4课时 授课人
教学目标 1.了解切线长的概念. 2.能证明切线长定理,并能用切线长定理进行计算和证明.
教学 重难点 教学重点:切线长定理及其运用. 教学难点:利用切线长定理解决相关问题.
教学活动
教学流程 师生活动 设计意图
课前小测 某广场有一个圆形的喷水池,如图中的圆环部分是喷水池的围墙.为了测量圆环的面积,小亮与小莹取来一根卷尺,拉直后使它与内圆相切,与外圆交于A,B两点,量得AB的长为12 m,你能由此求出圆环的面积吗 解:∵AB与小圆相切于点C, ∴OC垂直平分AB, ∴AC=AB=×12=6(m),∠ACO=90°. 在Rt△AOC中,OA2-OC2=AC2=62=36, ∴S圆环=π·(OA2-OC2)=36π(m2). 此题涉及切线的性质,垂径定理,勾股定理.
情境导入 问题:在☉O上任取一点A,过点A能作圆的几条切线 过圆上一点只能作一条切线. 让学生动手操作,感知如何过圆上一点画圆的切线.
合作探究 探究:切线长定理 问题1: 在情境导入图中☉O的切线上任取一点P,过点P作☉O的切线,能作几条 怎么作呢 解:把画出的图形沿直线PO对折,点A关于PO的对称点B在☉O上.连接PB,则PB与☉O相切,点B是切点,由PA与PB关于PO成轴对称,可以发现经过圆外一点可以画圆的两条切线PA,PB,并且PA=PB. 问题2:能证明上面结论是正确的吗 如图,已知P是☉O外一点,PA是☉O的切线.过切点A作PO的垂线,垂足为点C,交☉O于点B,连接PB,OA,OB. 解:∵OA=OB,OP⊥AB, ∴∠AOP=∠BOP. ∵OP=OP, ∴△OPA≌△OPB(SAS). ∵∠OAP=90°, ∴∠OBP=∠OAP=90°, ∴PB是☉O的切线,且PA=PB. 定义:经过圆外一点可以画圆的两条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的切线长. 归纳小结:切线长定理 过圆外一点所画的圆的两条切线长相等. 几何语言:∵PA,PB是圆的切线,∴PA=PB. 1.引导学生通过折叠,利用轴对称来得到另一条切线. 2.在证明切线长定理时,让学生理解PO平分两条切线的夹角,不要求记忆.
续表
合作探究 问题3:切线与切线长有区别吗 解:切线是直线,不能度量;切线长是线段的长,可以度量. 典例分析: 【例1】如图,P为☉O外一点,PA,PB是☉O的两条切线,A,B是切点,BC是☉O的直径. (1)求证:AC∥OP; (2)如果∠APB=70°,求的度数. (1)证明:如图,连接OA,AB,AB交PO于点D. ∵PA,PB分别切☉O于A,B两点, ∴OA=OB,PA=PB,OP=OP, ∴△AOP≌△BOP, ∴∠OPA=∠OPB,即PO平分∠APB, ∴PD⊥AB,∠PDA=90°. 又∵BC是☉O的直径, ∴∠CAB=90°, ∴AC∥OP. (2)解:∵PA=PB,∴∠PAB=∠PBA. ∵∠APB=70°, ∴∠PBA=(180°-∠APB)=(180°-70°)=55°. ∵BC是☉O的直径,∴∠CBP=90°. ∴∠ABC=∠CBP-∠PBA=90°-55°=35°. ∴的度数=2×∠ABC的度数=2×35°=70°. 【例2】 如图,P是☉O外一点,PA,PB分别和☉O切于A,B两点,PA=PB=4 cm,∠P=40°,C是劣弧AB上任意一点,过点C作☉O的切线,分别交PA,PB于点D,E,试求: (1)△PDE的周长; (2)∠DOE的度数. 解: (1)∵PA,PB,DE是☉O的切线, ∴PA=PB,AD=DC,EC=BE, ∴PD+PE+DE=PD+PE+DC+CE=PA+PB=8 cm, 即△PDE的周长为8 cm. (2)如图,连接OA,OB,OC. ∵PA,DE是☉O的切线,∴∠OAD=∠OCD=90°. 又∵OA=OC,OD=OD,∴Rt△ADO≌Rt△CDO, ∴∠DOA=∠DOC.同理∠COE=∠BOE, ∴∠DOE=∠AOB. ∵PA,PB是☉O的切线,∴∠OAP=∠OBP=90°, ∴∠AOB=180°-∠P=140°, ∴∠DOE=∠AOB=70°. 归纳小结:例1和例2都是切线长定理的应用,当已知一条切线时,连半径,得垂直.已知过圆外一点的两条切线时,重点用切线长定理的结论,切线长相等. 3.例1是一证二解,是几何综合题的常见形式,第二问的解答通常要用到第一问的结论.让学生体会辅助线的作用. 4.例2是切线长定理的典型应用,是易考题.利用切线长定理得到相等线段来转换.
续表
随堂检测 1.如图,正方形ABCD边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过点A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积是( D ) A.12 B.24 C.8 D.6 2.如图,PA,PB为☉O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交☉O于点D,下列结论不一定成立的是( D ) A.PA=PB B.∠BPD=∠APD C.AB⊥PD D.直线AB平分线段PD 3.如图,☉O分别切∠BAC的两边AB,AC于点E,F,点P在优弧上.若∠BAC=66°,则∠EPF= 57° . 4.如图,PA,PB是☉O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交☉O于点D. (1)求证:PO平分∠APC; (2)连接DB,若∠C=30°,求证:DB∥AC. 证明:(1)如图,连接OB. ∵PA,PB是☉O的切线, ∴PA=PB,PA⊥AO,PB⊥OB. ∵AO=BO,PO=PO. ∴Rt△PAO≌Rt△PBO, ∴∠APO=∠BPO,即PO平分∠APC. (2)由(1)知Rt△PAO≌Rt△PBO,∴∠AOP=∠BOP. ∵PB是☉O的切线,∴∠OBC=90°. ∵∠C=30°,∴∠BOC=60°,∴∠BOD=60°. 又∵OB=OD,∴∠OBD=60°,∴∠OBD=∠BOC,∴DB∥AC.
课堂小结 1.切线长是怎样定义的 2.切线长定理的内容是什么 3.切线与切线长有区别吗 区别在哪 便于学生梳理知识点,使知识更清晰条理.
作业布置 请完成教材练习题P98T1-T2
板书设计
切线长定理 1.切线长的定义. 2.切线长定理:过圆外一点所画的圆的两条切线长相等. 3.切线与切线长的区别:切线是直线,不能度量;切线长是线段的长,可以度量. 【例2】
教学反思
本节课是探索切线长定理及应用.先让学生通过折叠得到过圆外一点能作圆的两条切线,之后用演绎推理来证明过圆外一点的圆的两条切线长相等.讲授例1时,应先引导学生根据已知完成图形,与证明切线长定理的图形进行对比,要证平行,先连接OA,AB,由此使学生体会辅助线的作用.在证明切线长定理的过程中,要引导学生探索新的结论,会产生很多相等的角、弧、边,垂直的直线,等腰三角形,相似三角形等,建立新旧知识的联系.
课题 3.4 直线与圆的位置关系 课时 第1课时 授课人
教学目标 1.经历探索直线与圆的位置关系的过程. 2.通过观察得出“圆心到直线的距离d和半径r的数量关系”与“直线和圆的位置关系”,能进行位置关系与数量关系的相互转化.
教学 重难点 教学重点:直线与圆的位置关系. 教学难点:直线与圆的位置关系的判断方法.
教学活动
教学流程 师生活动 设计意图
课前小测 1.圆周角定理内容是什么 圆周角等于它所对弧上的圆心角的一半. 2.它的推论有哪些 推论1 圆周角的度数等于它所对弧的度数的一半. 推论2 同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等. 推论3 直径所对的圆周角是直角;90°的圆周角所对的弦是直径. 推论4 圆内接四边形的对角互补. 复习之前所学,加以巩固.
情境导入 问题一:在平面内一个点P与☉O的位置关系有几种 有三种.点在圆外;点在圆上;点在圆内. 问题二:已知☉O的半径为r,通过怎样的数量关系可以确定点P与☉O的位置关系 连接OP: (1)当OP>r时,点P在圆外; (2)当OP
续表
合作探究 ①当直线和圆有 两个 公共点时,这时我们说这条直线与圆 相交 ,这条直线叫做圆的 割线 ; ②当直线和圆有 唯一的 公共点时,这时我们说这条直线与圆 相切 ,这条直线叫做圆的 切线 ,这个点叫做 切点 ; ③当直线和圆 没有 公共点时,这时我们说这条直线与圆 相离 . (2)如图,设☉O的半径为r,圆心O到直线l的距离OP为d,直线与圆的位置关系与r和d的大小有关系吗 当直线l与☉O相交时,d
续表
随堂检测 3.已知☉O的半径为7,圆心O到直线AB的距离为d,根据条件填写d的范围: 若AB和☉O相离,则 d>7 ;若AB和☉O相切,则 d=7 ;若AB和☉O相交,则 d<7 . 4.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的取值情况是 3
通过表格,清晰且条理地展示出如何判断直线与圆的位置关系,巩固所学知识.
作业布置 请完成教材练习题P93T1-2
板书设计
直线与圆的位置关系 直线与圆位置关系的判断方法 1.交点个数. 2.d与r的关系: 当直线l与☉O相交时,d
教学反思
通过观察图形,引出直线与圆的三种不同的位置关系,并分别给出相交、相切、相离及割线、切线、切点的定义,引出圆的切线定义时,要使学生明白直线与圆“有唯一的公共点”的含义,探索直线与圆的三种位置关系与圆的半径r和圆心到直线的距离d之间的内在联系,实现了形与数的转化与统一.
课题 3.4 直线与圆的位置关系 课时 第2课时 授课人
教学目标 1.掌握切线的判定定理,培养学生的探索能力. 2.能运用切线的判定定理进行证明和计算.
教学重难点 教学重点:会用切线的判定定理进行证明和计算. 教学难点:选择正确的方法证明相切.
教学活动
教学流程 师生活动 设计意图
课前小测 1.直线与圆的位置关系有哪些 相交,相切,相离. 2.如何判断直线与圆的位置关系 (1)由直线与圆的交点个数判断:2个交点,相交;1个交点,相切;没有交点,相离. (2)由圆心到直线的距离d和半径r的关系判断: 当d>r时,相离;当d=r时,相切;当d
合作探究 探究:切线的判定定理 问题1:过☉O的半径OA的外端点A作与半径OA垂直的直线l(如图),你发现直线l与☉O有怎样的位置关系 为什么 解:相切. 因为圆心O到直线l的距离等于☉O的半径,所以直线l与☉O相切. 归纳小结: 切线的判定定理 过半径的外端并且垂直于半径的直线是圆的切线. 注意: “过半径的外端”和“垂直于半径”这两个条件缺一不可,否则就不是圆的切线. 问题2:利用上面的定理,过☉O上任意一点,你会用三角尺画☉O的切线吗 试一试. 解:设P是☉O上的任意一点,将三角尺的直角顶点与P点重合,一条直角边过圆心O,再沿另外一条直角边画直线,该直线便是☉O的经过点P的切线. 1.问题1让学生利用尺规作图,经过一点作已知直线的垂线,让学生发现是切线,并说出理由(d=r). 2.问题2先让学生尝试画图,通过交流,得到画法.
续表
合作探究 典例分析: 【例1】 如图,以△ABC的边AB为直径作☉O,如果☉O经过AC的中点D,然后过D作DE⊥BC,垂足为点E.DE是☉O的切线吗 说明理由. 解:DE是☉O的切线.理由如下:连接OD. ∵AB是☉O的直径,∴AO=OB. 又∵AD=DC, ∴OD是△ABC的中位线,从而OD∥BC. ∵DE⊥BC,∴DE⊥OD, ∴DE是☉O的切线. 在例1中,你还能由已知探索出哪些结论 说明你的理由. 解:连接BD. ∵AB是☉O的直径,∴BD⊥AC. 又∵D是AC的中点, ∴BD是AC的垂直平分线, ∴AB=BC,∠A=∠C. 【例2】 已知O为∠BAC平分线上一点,OD⊥AB于点D,以O点为圆心,OD为半径作☉O.求证:☉O与AC相切. 证明:过点O作OE⊥AC于点E. ∵AO平分∠BAC,OD⊥AB, ∴OE=OD, 即圆心O到AC的距离d=r, ∴AC是☉O切线. 讨论:例1和例2有何不同 归纳小结: 1.当已知条件中直线与圆有交点时,连接圆心和交点就作出了半径,相当于已知直线过半径的外端,只需要证明此直线垂直于半径即可得到结论.简记为“有交点,连半径,证垂直”. 2.从已知条件中读不出直线与圆有交点时,过圆心作直线的垂线段,证明垂线段等于半径(d=r),也可得到相切.简记为“无交点,作垂直,证半径”. 3.例1是连半径,证垂直,是切线判定的基础题型,也是中考的必考题,要让学生掌握方法. 4.例2是作垂直,证半径,是学生学习的难点,要掌握方法. 5.及时归纳应用切线的判定定理的思路的不同之处,找出关键点.让学生更清楚明白.
续表
随堂检测 1. 如图,AB是☉O的直径,点D在AB的延长线上,BD=OB,点C在☉O上,∠CAB=30°.求证:DC是☉O的切线. 证明:如图,连接OC,BC. ∵AB是☉O的直径,∴∠ACB=90°. ∵∠CAB=30°,∴∠ABC=60°. ∵OB=OC,∴△OBC为等边三角形, ∴∠OBC=60°,BC=OB=BD, ∴△BCD为等腰三角形,∠CBD=120°, ∴∠BCD=30°,∴∠OCD=∠OCB+∠BCD=90°, ∴DC是☉O的切线. 2.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AC于点E,以点O为圆心,OE长为半径作☉O.求证:AB是☉O的切线. 证明:如图,过点O作OF⊥AB于点F. ∵AB=AC,AO⊥BC,∴AO是∠BAC的平分线. ∵OE⊥AC,OF⊥AB,∴OF=OE, ∴AB是☉O的切线.
课堂小结 1.切线的判定方法有几种 2.切线的判定定理的内容是什么 应用定理时,需要注意什么 3.应用切线的判定定理有几种思路 是什么 便于学生梳理知识点,使知识更清晰条理.
作业布置 请完成教材练习题P94T1-T2
板书设计
切线的判定 1.切线的判定定理:过半径的外端并且垂直于半径的直线是圆的切线. 2.应用切线的判定定理的两种思路 (1)有交点,连半径,证垂直. (2)无交点,作垂直,证半径. 【例2】
教学反思
切线的判定定理是圆中的重点,是中考必考的内容.在学习这节课时,先让学生利用尺规作图发现直线是圆的切线并说出理由,从而得到切线的判定定理,教学时应提醒学生“过半径的外端”和“垂直于半径”这两个条件缺一不可,否则就不是圆的切线.这个定理是由“当d=r时,直线l与☉O相切”推出的.例1和例2可让学生独立思考,互相交流,发现它们的不同之处,总结关键点,以免在以后的证明中出现错误.
课题 3.4 直线与圆的位置关系 课时 第3课时 授课人
教学目标 1.经历探索切线的性质的过程,培养学生的探索能力. 2.会利用切线的性质解决相关的问题.
教学 重难点 教学重点:切线的性质定理的应用. 教学难点:用反证法证明切线的性质定理.
教学活动
教学流程 师生活动 设计意图
课前小测 切线的判定方法有哪些 (1)交点个数:当直线与圆有一个交点时,相切. (2)当圆心到直线的距离d=r时,相切. (3)过半径的外端并且垂直于半径的直线是圆的切线. 复习切线的判定方法,巩固旧知.
情境导入 问题1:你能说出切线的判定定理的逆命题吗 圆的切线垂直于经过切点的半径. 问题2:这个逆命题是真命题还是假命题 让学生通过画图对它的正确性作出猜想. 由学生说出切线的判定定理的逆命题,引出本节课的课题.
合作探究 探究:切线的性质定理 如果是真命题,你能给出证明吗 不好直接证明,用反证法能行吗 已知:如图,直线l与☉O相切于点A. 求证:OA⊥l. 证明:如图,假设l与半径OA不垂直.过点O作OB⊥直线l,垂足为点B.在l上取BA'=BA,且使B点在A与A'之间,连接OA'. 于是OB垂直平分AA',OA=OA'. ∵点A是切点,OA是☉O的半径, ∴OA'也是☉O的半径. 这就是说,直线l与☉O有两个公共点,即l与☉O相交,这与已知条件“直线l与☉O相切于点A”矛盾,所以OA⊥l. 归纳小结:切线的性质定理 圆的切线垂直于经过切点的半径. 几何语言:如图,l是☉O的切线,A为切点. ∵l是☉O的切线,A为切点, ∴OA⊥l. 切线的其他性质: (1)切线与圆只有一个交点; (2)圆心到切线的距离等于圆的半径. 1.引导学生尝试证明,当发现用直接证明不好解决时,尝试用反证法证明.
续表
合作探究 典例分析: 【例1】 已知A,B,C是☉O上的三点,经过点A,点B分别作☉O的切线,两切线相交于点P,如果∠P=42°,求∠ACB的度数. 解:(1)如图①,当点C在上时,连接OA,OB. ∵PA,PB是☉O的切线,A,B是切点, ∴∠OAP=∠OBP=90°. 在四边形OAPB中,∵∠P=42°, ∴∠AOB=360°-∠OAP-∠OBP-∠P=360°-90°-90°-42°=138°, ∴∠ACB=∠AOB=×138°=69°. (2)如图②,当点C在劣弧上时,在优弧上任取一点C',连接AC',BC'. 由(1)知,∠AC'B=69°. 在圆内接四边形ACBC'中, ∵∠ACB+∠AC'B=180°, ∴∠ACB=180°-∠AC'B=180°-69°=111°. ① ② 【例2】 如图,△ABC内接于☉O,AB是☉O的直径,点D在☉O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.求证:DC=BC. 证明:如图,连接OC. ∵CE是☉O的切线,∴OC⊥CE. ∵AE⊥CE,∴OC∥AE,∴∠OCA=∠EAC. ∵OC=OA,∴∠OCA=∠OAC,∴∠EAC=OAC, ∴=,∴DC=BC. 你还有其他的方法吗 2.例1是一题多解题,是易错题,易考题,要考虑周全. 3.例2采用不同的方法来完成证明,第二个方法侧重于垂径定理的推论“知二推三”的应用.
随堂检测 1.如图,AB是☉O的弦,AC是☉O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( D ) A.20° B.25° C.40° D.50° 2.如图,☉M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C,则圆心M的坐标是 (5,4) .
续表
随堂检测 3.如图,在△ABC中,BC是以AB为直径的☉O的切线,且☉O与AC相交于点D,E为BC的中点,连接DE.求证:DE是☉O的切线. 证明:如图,连接OD,BD. ∵OD=OB,∴∠ODB=∠OBD. ∵AB是☉O的直径, ∴∠ADB=90°, ∴∠CDB=90°. ∵E为BC的中点, ∴DE=BE, ∴∠EDB=∠EBD, ∴∠ODB+∠EDB=∠OBD+∠EBD, 即∠EDO=∠EBO. ∵BC是以AB为直径的☉O的切线, ∴AB⊥BC,∴∠EBO=90°, ∴∠ODE=90°, ∴DE是☉O的切线.
课堂小结 1.切线的性质有哪些 2.在已知圆的切线的条件下,一般怎样做 让学生熟记切线的性质定理,知切线,连半径,得垂直.
作业布置 请完成教材练习题P96T1-T2
板书设计
切线的性质 1.切线的性质定理:圆的切线垂直于经过切点的半径. 几何语言:如图,l是☉O的切线,A为切点. ∵l是☉O的切线,A为切点, ∴OA⊥l. 2.切线的其他性质 (1)切线与圆只有一个交点; (2)圆心到切线的距离等于圆的半径. 【例2】
教学反思
本节课先引导学生复习切线的判定定理,再让学生说出它的逆命题,通过画图作出猜想.在用直接证明法不好证明时,尝试用反证法进行证明,对学生来说是个难点.学生对反证法证明的思路和实质还缺乏真正的理解,因此往往停留在形式的模仿上,在讲解时,速度要慢,不断加深对这个方法的认识.例1是一题多解,点C在优弧还是劣弧上不能确定时,一定要分情况讨论.例2综合性强一些,考察切线的性质,圆周角定理的推论,垂径定理的推论的应用.
课题 3.4 直线与圆的位置关系 课时 第4课时 授课人
教学目标 1.了解切线长的概念. 2.能证明切线长定理,并能用切线长定理进行计算和证明.
教学 重难点 教学重点:切线长定理及其运用. 教学难点:利用切线长定理解决相关问题.
教学活动
教学流程 师生活动 设计意图
课前小测 某广场有一个圆形的喷水池,如图中的圆环部分是喷水池的围墙.为了测量圆环的面积,小亮与小莹取来一根卷尺,拉直后使它与内圆相切,与外圆交于A,B两点,量得AB的长为12 m,你能由此求出圆环的面积吗 解:∵AB与小圆相切于点C, ∴OC垂直平分AB, ∴AC=AB=×12=6(m),∠ACO=90°. 在Rt△AOC中,OA2-OC2=AC2=62=36, ∴S圆环=π·(OA2-OC2)=36π(m2). 此题涉及切线的性质,垂径定理,勾股定理.
情境导入 问题:在☉O上任取一点A,过点A能作圆的几条切线 过圆上一点只能作一条切线. 让学生动手操作,感知如何过圆上一点画圆的切线.
合作探究 探究:切线长定理 问题1: 在情境导入图中☉O的切线上任取一点P,过点P作☉O的切线,能作几条 怎么作呢 解:把画出的图形沿直线PO对折,点A关于PO的对称点B在☉O上.连接PB,则PB与☉O相切,点B是切点,由PA与PB关于PO成轴对称,可以发现经过圆外一点可以画圆的两条切线PA,PB,并且PA=PB. 问题2:能证明上面结论是正确的吗 如图,已知P是☉O外一点,PA是☉O的切线.过切点A作PO的垂线,垂足为点C,交☉O于点B,连接PB,OA,OB. 解:∵OA=OB,OP⊥AB, ∴∠AOP=∠BOP. ∵OP=OP, ∴△OPA≌△OPB(SAS). ∵∠OAP=90°, ∴∠OBP=∠OAP=90°, ∴PB是☉O的切线,且PA=PB. 定义:经过圆外一点可以画圆的两条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的切线长. 归纳小结:切线长定理 过圆外一点所画的圆的两条切线长相等. 几何语言:∵PA,PB是圆的切线,∴PA=PB. 1.引导学生通过折叠,利用轴对称来得到另一条切线. 2.在证明切线长定理时,让学生理解PO平分两条切线的夹角,不要求记忆.
续表
合作探究 问题3:切线与切线长有区别吗 解:切线是直线,不能度量;切线长是线段的长,可以度量. 典例分析: 【例1】如图,P为☉O外一点,PA,PB是☉O的两条切线,A,B是切点,BC是☉O的直径. (1)求证:AC∥OP; (2)如果∠APB=70°,求的度数. (1)证明:如图,连接OA,AB,AB交PO于点D. ∵PA,PB分别切☉O于A,B两点, ∴OA=OB,PA=PB,OP=OP, ∴△AOP≌△BOP, ∴∠OPA=∠OPB,即PO平分∠APB, ∴PD⊥AB,∠PDA=90°. 又∵BC是☉O的直径, ∴∠CAB=90°, ∴AC∥OP. (2)解:∵PA=PB,∴∠PAB=∠PBA. ∵∠APB=70°, ∴∠PBA=(180°-∠APB)=(180°-70°)=55°. ∵BC是☉O的直径,∴∠CBP=90°. ∴∠ABC=∠CBP-∠PBA=90°-55°=35°. ∴的度数=2×∠ABC的度数=2×35°=70°. 【例2】 如图,P是☉O外一点,PA,PB分别和☉O切于A,B两点,PA=PB=4 cm,∠P=40°,C是劣弧AB上任意一点,过点C作☉O的切线,分别交PA,PB于点D,E,试求: (1)△PDE的周长; (2)∠DOE的度数. 解: (1)∵PA,PB,DE是☉O的切线, ∴PA=PB,AD=DC,EC=BE, ∴PD+PE+DE=PD+PE+DC+CE=PA+PB=8 cm, 即△PDE的周长为8 cm. (2)如图,连接OA,OB,OC. ∵PA,DE是☉O的切线,∴∠OAD=∠OCD=90°. 又∵OA=OC,OD=OD,∴Rt△ADO≌Rt△CDO, ∴∠DOA=∠DOC.同理∠COE=∠BOE, ∴∠DOE=∠AOB. ∵PA,PB是☉O的切线,∴∠OAP=∠OBP=90°, ∴∠AOB=180°-∠P=140°, ∴∠DOE=∠AOB=70°. 归纳小结:例1和例2都是切线长定理的应用,当已知一条切线时,连半径,得垂直.已知过圆外一点的两条切线时,重点用切线长定理的结论,切线长相等. 3.例1是一证二解,是几何综合题的常见形式,第二问的解答通常要用到第一问的结论.让学生体会辅助线的作用. 4.例2是切线长定理的典型应用,是易考题.利用切线长定理得到相等线段来转换.
续表
随堂检测 1.如图,正方形ABCD边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过点A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积是( D ) A.12 B.24 C.8 D.6 2.如图,PA,PB为☉O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交☉O于点D,下列结论不一定成立的是( D ) A.PA=PB B.∠BPD=∠APD C.AB⊥PD D.直线AB平分线段PD 3.如图,☉O分别切∠BAC的两边AB,AC于点E,F,点P在优弧上.若∠BAC=66°,则∠EPF= 57° . 4.如图,PA,PB是☉O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交☉O于点D. (1)求证:PO平分∠APC; (2)连接DB,若∠C=30°,求证:DB∥AC. 证明:(1)如图,连接OB. ∵PA,PB是☉O的切线, ∴PA=PB,PA⊥AO,PB⊥OB. ∵AO=BO,PO=PO. ∴Rt△PAO≌Rt△PBO, ∴∠APO=∠BPO,即PO平分∠APC. (2)由(1)知Rt△PAO≌Rt△PBO,∴∠AOP=∠BOP. ∵PB是☉O的切线,∴∠OBC=90°. ∵∠C=30°,∴∠BOC=60°,∴∠BOD=60°. 又∵OB=OD,∴∠OBD=60°,∴∠OBD=∠BOC,∴DB∥AC.
课堂小结 1.切线长是怎样定义的 2.切线长定理的内容是什么 3.切线与切线长有区别吗 区别在哪 便于学生梳理知识点,使知识更清晰条理.
作业布置 请完成教材练习题P98T1-T2
板书设计
切线长定理 1.切线长的定义. 2.切线长定理:过圆外一点所画的圆的两条切线长相等. 3.切线与切线长的区别:切线是直线,不能度量;切线长是线段的长,可以度量. 【例2】
教学反思
本节课是探索切线长定理及应用.先让学生通过折叠得到过圆外一点能作圆的两条切线,之后用演绎推理来证明过圆外一点的圆的两条切线长相等.讲授例1时,应先引导学生根据已知完成图形,与证明切线长定理的图形进行对比,要证平行,先连接OA,AB,由此使学生体会辅助线的作用.在证明切线长定理的过程中,要引导学生探索新的结论,会产生很多相等的角、弧、边,垂直的直线,等腰三角形,相似三角形等,建立新旧知识的联系.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
