3.5 三角形的内切圆 教案 (表格式) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 3.5 三角形的内切圆 教案 (表格式) 2025-2026学年数学青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:41:48 | ||
图片预览



文档简介
3.5 三角形的内切圆
课题 3.5 三角形的内切圆 课时 1课时 授课人
教学目标 1.了解三角形的内切圆、三角形的内心、圆的外切三角形的概念. 2.会利用基本作图作三角形的内切圆. 3.了解三角形内心的性质,并会进行有关的计算.
教学 重难点 教学重点:三角形内切圆的有关概念和画法. 教学难点:三角形内切圆有关性质的应用.
教学活动
教学流程 师生活动 设计意图
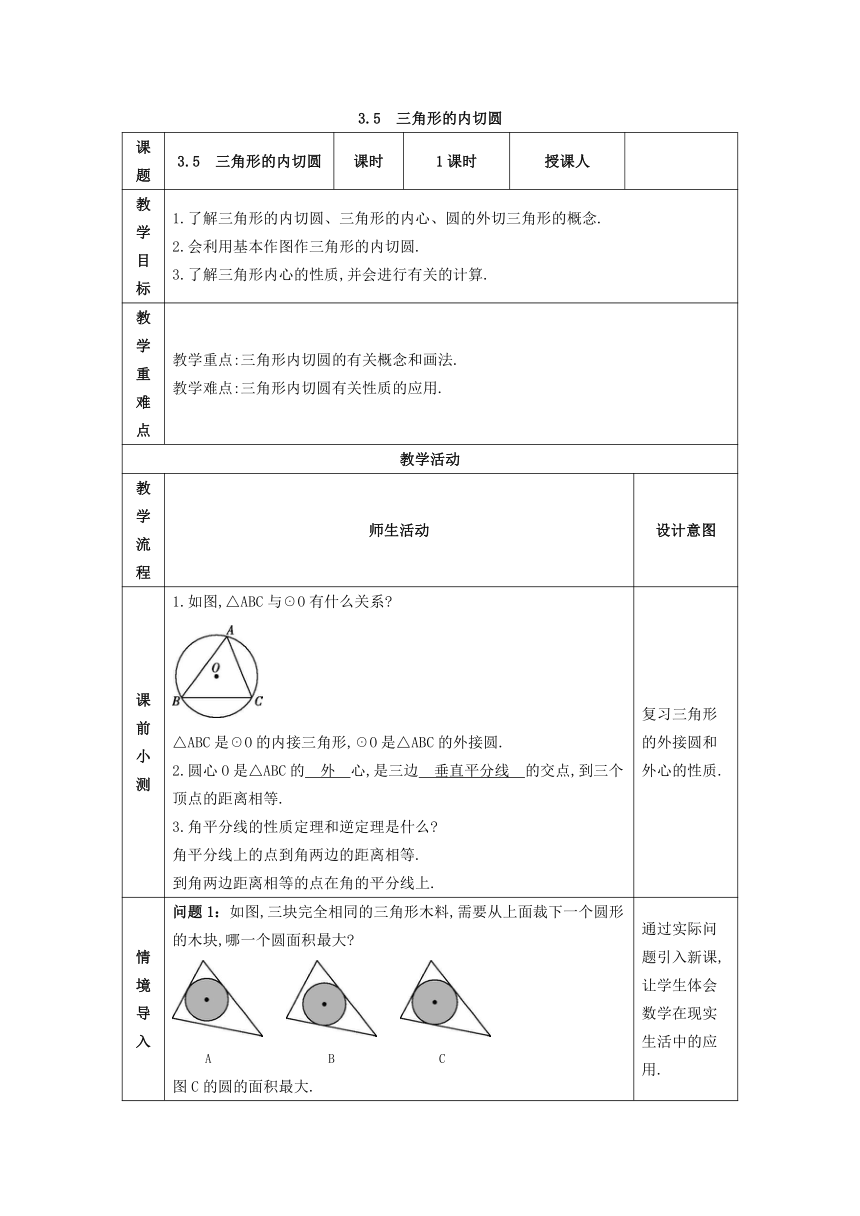
课前小测 1.如图,△ABC与☉O有什么关系 △ABC是☉O的内接三角形,☉O是△ABC的外接圆. 2.圆心O是△ABC的 外 心,是三边 垂直平分线 的交点,到三个顶点的距离相等. 3.角平分线的性质定理和逆定理是什么 角平分线上的点到角两边的距离相等. 到角两边距离相等的点在角的平分线上. 复习三角形的外接圆和外心的性质.
情境导入 问题1:如图,三块完全相同的三角形木料,需要从上面裁下一个圆形的木块,哪一个圆面积最大 A B C 图C的圆的面积最大. 问题2:同学们你知道怎样正确画出裁剪图吗 这就是本节课要探究的内容. 通过实际问题引入新课,让学生体会数学在现实生活中的应用.
合作探究 探究:三角形的内切圆 问题1:如图,在∠AOB内作圆,使其与两边OA,OB都相切,满足上述条件的圆是否可以作出 如果可以作出,能作多少个 所作出的圆的圆心的位置有什么特征 解:满足上述条件的圆可以作出,并且可以作无数个.其中每个圆的圆心到∠AOB的两边的距离都分别相等,所以这些圆的圆心都在∠AOB的平分线上. 问题2:任意作一个△ABC,如果在△ABC内作圆,使其与各边都相切,满足上述条件的圆是否可以作出 如果可以作出,能作多少个 所作出的圆的圆心位置有什么特征 解:可以作出. 由问题1可知,圆心在角的平分线上,而三角形的三条角平分线相交于同一点,只需作任意两个角的平分线,交点即为圆心,所以只能作一个. 因为任意三角形的三条角平分线的交点都在三角形内部,所以圆心只能在三角形内部. 1.引导学生通过画图、观察、思考,感悟作三角形一个角的平分线,引出三角形内切圆的作法. 2.在问题2中引导学生探究问题,通过分析寻找作图的思路,可让学生回忆三角形角平分线的性质,进而让学生根据证明的过程发现作法.
续表
合作探究 问题3:怎样用尺规作一个圆,使它与△ABC的各边都相切呢 已知:△ABC(如图). 求作:☉I,使它与△ABC各边都相切. 作法:1.作∠B,∠C的平分线BD,CE,BD与CE相交于点I(如图); 2.过点I作IF⊥BC,垂足为点F; 3.以I为圆心,IF为半径作圆. ☉I就是所求作的圆. 问题4:你能说出上面作图的道理吗 与三角形各边都相切的圆有几个 解:由作法可知,与三角形的各边都相切的圆能作并且只能作出一个. 三角形的内心是三角形的三条角平分线的交点,它到三角形各边的距离相等.任何一个三角形都有且只有一个内心,三角形的内心在三角形的内部. 定义:与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形. 典例分析: 【例1】 如图,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于E,F两点,则( C ) A.EF>AE+BF B.EF续表
合作探究 【例2】 如图,在△ABC中,∠A=68°,点I是内心. (1)求∠BIC的度数. (2)若∠A=50°,则∠BIC= . (3)若∠BIC=120°,则∠A= . 解:(1)∵点I是△ABC的内心, ∴∠1=∠ABC,∠2=∠ACB. 因而∠1+∠2=(∠ABC+∠ACB) =(180°-∠A) =(180°-68°)=56°, ∴∠BIC=180°-(∠1+∠2)=180°-56°=124°. (2)115° (3)60° 归纳小结: 三角形的内心是三条角平分线的交点,所以三角形的内心已知时,三角形顶点和内心的连线平分三角形的内角.例2利用了这一性质和三角形内角和定理. 如果在△ABC中,点I是内心,那么∠BIC=90°+∠A.
随堂检测 1.如图,△ABC的内切圆O与各边分别相切于点D,E,F,则点O是△DEF的( D ) A.三条中线的交点 B.三条高的交点 C.三条角平分线的交点 D.三条边的垂直平分线的交点 2.如图,△ABC的内切圆☉O与BC,CA,AB分别相切于点D,E,F,且AB=9 cm,BC=14 cm,CA=13 cm,则AF的长为( B ) A.3 cm B.4 cm C.5 cm D.9 cm 3.如图,在△ABC中,∠A=50°.当点O是内心时,∠BOC= 115° ;当点O是外心时,∠BOC= 100° .
续表
随堂检测 4. 如图,已知△ABC的三边长分别为a,b,c,它的内切圆半径为r,切点分别为D,E,F.求△ABC的面积. 解:如图,连接OA,OB,OC,OD,OE,OF. ∵☉O是△ABC的是内切圆, ∴OE⊥a,同理OD⊥c,OF⊥b, ∴S△ABC=S△BOC+S△AOC+S△AOB =ar+br+cr =r(a+b+c).
课堂小结 1.如图,△ABC是☉O的 三角形,☉O是△ABC的 圆,点O叫△ABC的 ,它是三角形 的交点,到 的距离相等,∠BOC= ∠A. 2.如图,△DEF是☉I的 三角形,☉I是△DEF的 圆,点I是△DEF的 心,它是三角形 的交点,到 的距离相等,∠EIF与∠D之间的数量关系是 . 3.直角三角形内切圆半径r和三边有怎样的关系 以问题的形式进行比较,加深学生对三角形的外心与内心的理解,便于学生对本节课的知识进行及时整理和归纳.
作业布置 请完成教材练习题P103T1-T2
板书设计
三角形的内切圆 1.定义:三角形的内切圆,三角形的内心,圆的外切三角形. 2.三角形的内心的性质. 【例2】 3.结论:如果在△ABC中,点I是内心,那么∠BIC=90°+∠A. 4.直角三角形内切圆半径r和三边关系:r=.
教学反思
本节课让学生通过作图和思考发现与一个角的两边都相切的圆的圆心都在角的内部,由于圆心到角的两边的距离相等,所以与角的两边都相切的圆的圆心在这个角的平分线上,这样的圆能作无数个.之后引出与三角形的三边都相切的圆的圆心应满足的条件:一是圆心在三角形内;二是到三边的距离相等,得出作法.内心是角平分线的交点.让学生明白任意一个三角形都有且只有一个内心和一个外心,是两个不同的概念.
课题 3.5 三角形的内切圆 课时 1课时 授课人
教学目标 1.了解三角形的内切圆、三角形的内心、圆的外切三角形的概念. 2.会利用基本作图作三角形的内切圆. 3.了解三角形内心的性质,并会进行有关的计算.
教学 重难点 教学重点:三角形内切圆的有关概念和画法. 教学难点:三角形内切圆有关性质的应用.
教学活动
教学流程 师生活动 设计意图
课前小测 1.如图,△ABC与☉O有什么关系 △ABC是☉O的内接三角形,☉O是△ABC的外接圆. 2.圆心O是△ABC的 外 心,是三边 垂直平分线 的交点,到三个顶点的距离相等. 3.角平分线的性质定理和逆定理是什么 角平分线上的点到角两边的距离相等. 到角两边距离相等的点在角的平分线上. 复习三角形的外接圆和外心的性质.
情境导入 问题1:如图,三块完全相同的三角形木料,需要从上面裁下一个圆形的木块,哪一个圆面积最大 A B C 图C的圆的面积最大. 问题2:同学们你知道怎样正确画出裁剪图吗 这就是本节课要探究的内容. 通过实际问题引入新课,让学生体会数学在现实生活中的应用.
合作探究 探究:三角形的内切圆 问题1:如图,在∠AOB内作圆,使其与两边OA,OB都相切,满足上述条件的圆是否可以作出 如果可以作出,能作多少个 所作出的圆的圆心的位置有什么特征 解:满足上述条件的圆可以作出,并且可以作无数个.其中每个圆的圆心到∠AOB的两边的距离都分别相等,所以这些圆的圆心都在∠AOB的平分线上. 问题2:任意作一个△ABC,如果在△ABC内作圆,使其与各边都相切,满足上述条件的圆是否可以作出 如果可以作出,能作多少个 所作出的圆的圆心位置有什么特征 解:可以作出. 由问题1可知,圆心在角的平分线上,而三角形的三条角平分线相交于同一点,只需作任意两个角的平分线,交点即为圆心,所以只能作一个. 因为任意三角形的三条角平分线的交点都在三角形内部,所以圆心只能在三角形内部. 1.引导学生通过画图、观察、思考,感悟作三角形一个角的平分线,引出三角形内切圆的作法. 2.在问题2中引导学生探究问题,通过分析寻找作图的思路,可让学生回忆三角形角平分线的性质,进而让学生根据证明的过程发现作法.
续表
合作探究 问题3:怎样用尺规作一个圆,使它与△ABC的各边都相切呢 已知:△ABC(如图). 求作:☉I,使它与△ABC各边都相切. 作法:1.作∠B,∠C的平分线BD,CE,BD与CE相交于点I(如图); 2.过点I作IF⊥BC,垂足为点F; 3.以I为圆心,IF为半径作圆. ☉I就是所求作的圆. 问题4:你能说出上面作图的道理吗 与三角形各边都相切的圆有几个 解:由作法可知,与三角形的各边都相切的圆能作并且只能作出一个. 三角形的内心是三角形的三条角平分线的交点,它到三角形各边的距离相等.任何一个三角形都有且只有一个内心,三角形的内心在三角形的内部. 定义:与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形. 典例分析: 【例1】 如图,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于E,F两点,则( C ) A.EF>AE+BF B.EF
合作探究 【例2】 如图,在△ABC中,∠A=68°,点I是内心. (1)求∠BIC的度数. (2)若∠A=50°,则∠BIC= . (3)若∠BIC=120°,则∠A= . 解:(1)∵点I是△ABC的内心, ∴∠1=∠ABC,∠2=∠ACB. 因而∠1+∠2=(∠ABC+∠ACB) =(180°-∠A) =(180°-68°)=56°, ∴∠BIC=180°-(∠1+∠2)=180°-56°=124°. (2)115° (3)60° 归纳小结: 三角形的内心是三条角平分线的交点,所以三角形的内心已知时,三角形顶点和内心的连线平分三角形的内角.例2利用了这一性质和三角形内角和定理. 如果在△ABC中,点I是内心,那么∠BIC=90°+∠A.
随堂检测 1.如图,△ABC的内切圆O与各边分别相切于点D,E,F,则点O是△DEF的( D ) A.三条中线的交点 B.三条高的交点 C.三条角平分线的交点 D.三条边的垂直平分线的交点 2.如图,△ABC的内切圆☉O与BC,CA,AB分别相切于点D,E,F,且AB=9 cm,BC=14 cm,CA=13 cm,则AF的长为( B ) A.3 cm B.4 cm C.5 cm D.9 cm 3.如图,在△ABC中,∠A=50°.当点O是内心时,∠BOC= 115° ;当点O是外心时,∠BOC= 100° .
续表
随堂检测 4. 如图,已知△ABC的三边长分别为a,b,c,它的内切圆半径为r,切点分别为D,E,F.求△ABC的面积. 解:如图,连接OA,OB,OC,OD,OE,OF. ∵☉O是△ABC的是内切圆, ∴OE⊥a,同理OD⊥c,OF⊥b, ∴S△ABC=S△BOC+S△AOC+S△AOB =ar+br+cr =r(a+b+c).
课堂小结 1.如图,△ABC是☉O的 三角形,☉O是△ABC的 圆,点O叫△ABC的 ,它是三角形 的交点,到 的距离相等,∠BOC= ∠A. 2.如图,△DEF是☉I的 三角形,☉I是△DEF的 圆,点I是△DEF的 心,它是三角形 的交点,到 的距离相等,∠EIF与∠D之间的数量关系是 . 3.直角三角形内切圆半径r和三边有怎样的关系 以问题的形式进行比较,加深学生对三角形的外心与内心的理解,便于学生对本节课的知识进行及时整理和归纳.
作业布置 请完成教材练习题P103T1-T2
板书设计
三角形的内切圆 1.定义:三角形的内切圆,三角形的内心,圆的外切三角形. 2.三角形的内心的性质. 【例2】 3.结论:如果在△ABC中,点I是内心,那么∠BIC=90°+∠A. 4.直角三角形内切圆半径r和三边关系:r=.
教学反思
本节课让学生通过作图和思考发现与一个角的两边都相切的圆的圆心都在角的内部,由于圆心到角的两边的距离相等,所以与角的两边都相切的圆的圆心在这个角的平分线上,这样的圆能作无数个.之后引出与三角形的三边都相切的圆的圆心应满足的条件:一是圆心在三角形内;二是到三边的距离相等,得出作法.内心是角平分线的交点.让学生明白任意一个三角形都有且只有一个内心和一个外心,是两个不同的概念.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
