福建省泉州市2024-2025学年高一下学期7月期末考试 数学试卷(PDF版,含答案)
文档属性
| 名称 | 福建省泉州市2024-2025学年高一下学期7月期末考试 数学试卷(PDF版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览




文档简介
16.(15分)
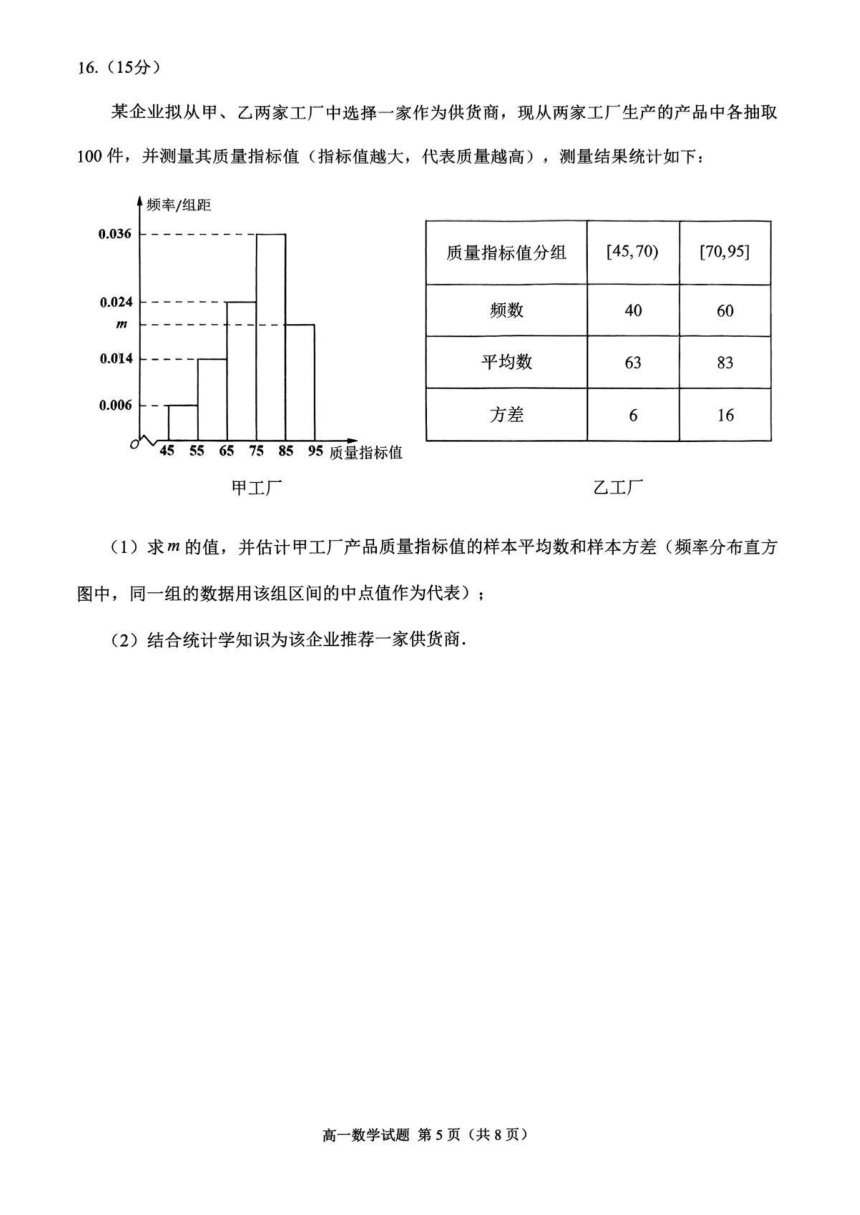
某企业拟从甲、乙两家工厂中选择一家作为供货商,现从两家工厂生产的产品中各抽取
100件,并测量其质量指标值(指标值越大,代表质量越高),测量结果统计如下:
个频率/组距
0.036
质量指标值分组
[45,70)
[70,95]
0.024
频数
40
60
m
0.014
平均数
63
83
0.006
方差
6
16
0V455565758595质量指标值
甲工厂
乙工厂
(1)求m的值,并估计甲工厂产品质量指标值的样本平均数和样本方差(频率分布直方
图中,同一组的数据用该组区间的中点值作为代表);
(2)结合统计学知识为该企业推荐一家供货商。
高一数学试题第5页(共8页)
17.(15分)
如图1,在平行四边形ABCD中,AB=2,BC=1,AC⊥BC,将△ACD沿AC翻折至
△ACP(如图2),使得PB=√5.
(1)证明:BC⊥平面PAC:
(2)求直线AB与平面PBC所成的角的正弦值:
(3)若点E在平面ABC内,AE⊥BE,当三棱锥P-ABE的体积最大时,求AE的长
D
B
图1
图2
高一数学试题第6页(共8页)
18.(17分)
己知锐角△ABC的内角A,B,C所对的边分别为a,b,c,且b2+c2=a2+bc·
(1)求A:
(2)若c=4,求△ABC的面积的取值范围;
(3)如图,若D为△MBC外-点,且∠ABD=∠ACB=寻BDLCD,.AD=i店,求a.
B
C
19.(17分)
在平面直角坐标系xOy中,点P(x,y)绕原点O逆时针旋转a角后得到点P'(x',y),其中
x'=c--ys血2称该公式为点的坐标旋转变换公式。
y'=xsina+ycosa,
(1)已知点A,0)可由点4(a,b)绕原点0逆时针旋转C得到,求a,b的值:
2
(2)若曲线C:y=
n2x绕原点O逆时针旋转牙得到曲线C,求证:直线y=X+1与
2
C有无数多个公共点;
(3)曲线E:y-x=Cos(x+y)上是否存在四个点,使得以这四个点为顶点的四边形为等腰
梯形?证明你的结论.
2024一2025学年度下学期泉州市高中教学质量监测
2025.07
高一数学参考答案及评分细则
1
3
5
6
7
8
9
10
11
B
D
C
C
B
A
Y
C
AC
ABD
ACD
12.9
13.
14.4,20-87
15(13分)【试题解析】
(1)依题意得f()的最小正周期为T=2江-2
2分
由2-2+≤2m*
ez,
(k∈Z没写扣1分)
4分
解得m-C≤x≤k+正,keZ,
12
5分
12
所以函数f(x)的单调递增区间[饥-
5π
(没写成区间形式扣1分,写成开区间不扣分)
6分
2)由xe0孕.得2x+
7分
所以sm2x+孕,
8分
所以f)=2sin(2x+∈L,2],
9分
解法一:当x∈[0,京时,由mW()9,且f)∈L,2],得m≤
f(x)
10分
只需满足≤
1
f(x)
11分
因为函数y=上在区间L,2]上单调递减,
1
1
所以
12分
f(x))min
2
所以≤;,即实数m的取值范围为(-0,习
.…13分
解法二:令t=f(x)1≤t≤2),可设8()=t,则原题意等价于8()1,…10分
高一数学试题第1页(共10页)
某企业拟从甲、乙两家工厂中选择一家作为供货商,现从两家工厂生产的产品中各抽取
100件,并测量其质量指标值(指标值越大,代表质量越高),测量结果统计如下:
个频率/组距
0.036
质量指标值分组
[45,70)
[70,95]
0.024
频数
40
60
m
0.014
平均数
63
83
0.006
方差
6
16
0V455565758595质量指标值
甲工厂
乙工厂
(1)求m的值,并估计甲工厂产品质量指标值的样本平均数和样本方差(频率分布直方
图中,同一组的数据用该组区间的中点值作为代表);
(2)结合统计学知识为该企业推荐一家供货商。
高一数学试题第5页(共8页)
17.(15分)
如图1,在平行四边形ABCD中,AB=2,BC=1,AC⊥BC,将△ACD沿AC翻折至
△ACP(如图2),使得PB=√5.
(1)证明:BC⊥平面PAC:
(2)求直线AB与平面PBC所成的角的正弦值:
(3)若点E在平面ABC内,AE⊥BE,当三棱锥P-ABE的体积最大时,求AE的长
D
B
图1
图2
高一数学试题第6页(共8页)
18.(17分)
己知锐角△ABC的内角A,B,C所对的边分别为a,b,c,且b2+c2=a2+bc·
(1)求A:
(2)若c=4,求△ABC的面积的取值范围;
(3)如图,若D为△MBC外-点,且∠ABD=∠ACB=寻BDLCD,.AD=i店,求a.
B
C
19.(17分)
在平面直角坐标系xOy中,点P(x,y)绕原点O逆时针旋转a角后得到点P'(x',y),其中
x'=c--ys血2称该公式为点的坐标旋转变换公式。
y'=xsina+ycosa,
(1)已知点A,0)可由点4(a,b)绕原点0逆时针旋转C得到,求a,b的值:
2
(2)若曲线C:y=
n2x绕原点O逆时针旋转牙得到曲线C,求证:直线y=X+1与
2
C有无数多个公共点;
(3)曲线E:y-x=Cos(x+y)上是否存在四个点,使得以这四个点为顶点的四边形为等腰
梯形?证明你的结论.
2024一2025学年度下学期泉州市高中教学质量监测
2025.07
高一数学参考答案及评分细则
1
3
5
6
7
8
9
10
11
B
D
C
C
B
A
Y
C
AC
ABD
ACD
12.9
13.
14.4,20-87
15(13分)【试题解析】
(1)依题意得f()的最小正周期为T=2江-2
2分
由2-2+≤2m*
ez,
(k∈Z没写扣1分)
4分
解得m-C≤x≤k+正,keZ,
12
5分
12
所以函数f(x)的单调递增区间[饥-
5π
(没写成区间形式扣1分,写成开区间不扣分)
6分
2)由xe0孕.得2x+
7分
所以sm2x+孕,
8分
所以f)=2sin(2x+∈L,2],
9分
解法一:当x∈[0,京时,由mW()9,且f)∈L,2],得m≤
f(x)
10分
只需满足≤
1
f(x)
11分
因为函数y=上在区间L,2]上单调递减,
1
1
所以
12分
f(x))min
2
所以≤;,即实数m的取值范围为(-0,习
.…13分
解法二:令t=f(x)1≤t≤2),可设8()=t,则原题意等价于8()1,…10分
高一数学试题第1页(共10页)
同课章节目录
