第2章对称图形-圆同步练习卷(含答案)-数学九年级上册苏科版
文档属性
| 名称 | 第2章对称图形-圆同步练习卷(含答案)-数学九年级上册苏科版 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第2章对称图形-圆同步练习卷-数学九年级上册苏科版
一.选择题(共9小题)
1.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
2.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
3.(2025春 鄞州区校级月考)一个圆锥的底面直径是8,母线长是7,则圆锥的侧面积是( )
A.16π B.28π C.42π D.56π
4.(2024秋 滨江区期末)如图,线段AE是⊙O的直径,点B是⊙O上一点,设∠DAE=α,∠DCB=β.若AE⊥BC,BD=GD,则( )
A.3α+β=270° B.α+β=180° C.3β﹣α=270° D.β﹣α=90°
5.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
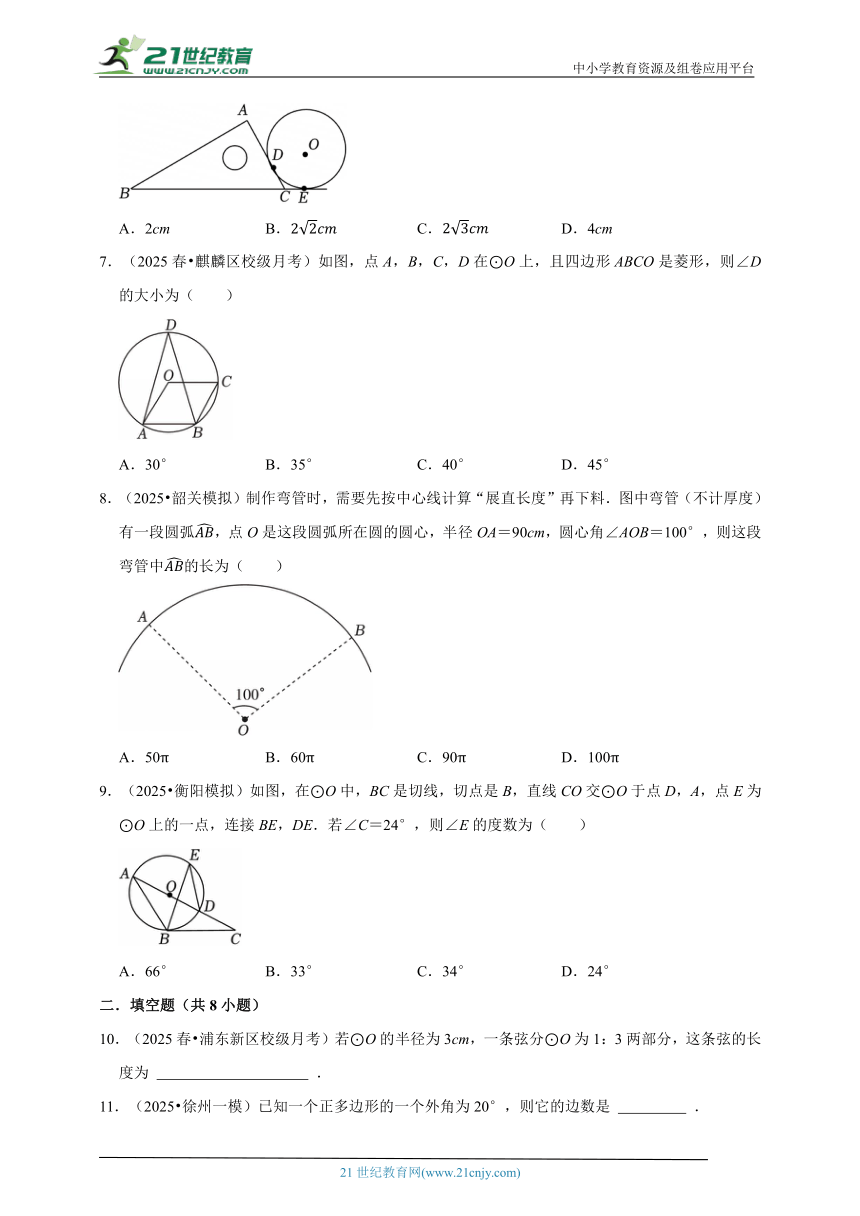
6.(2025春 琼海校级月考)如图,小珍同学借助直角三角板(∠ACB=60°)测量纸杯底面圆O的半径,圆O与边AC相切于点D,与BC的延长线相切于点E,测得CE=2cm,则底面圆O的半径为( )
A.2cm B. C. D.4cm
7.(2025春 麒麟区校级月考)如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
8.(2025 韶关模拟)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
9.(2025 衡阳模拟)如图,在⊙O中,BC是切线,切点是B,直线CO交⊙O于点D,A,点E为⊙O上的一点,连接BE,DE.若∠C=24°,则∠E的度数为( )
A.66° B.33° C.34° D.24°
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
11.(2025 徐州一模)已知一个正多边形的一个外角为20°,则它的边数是 .
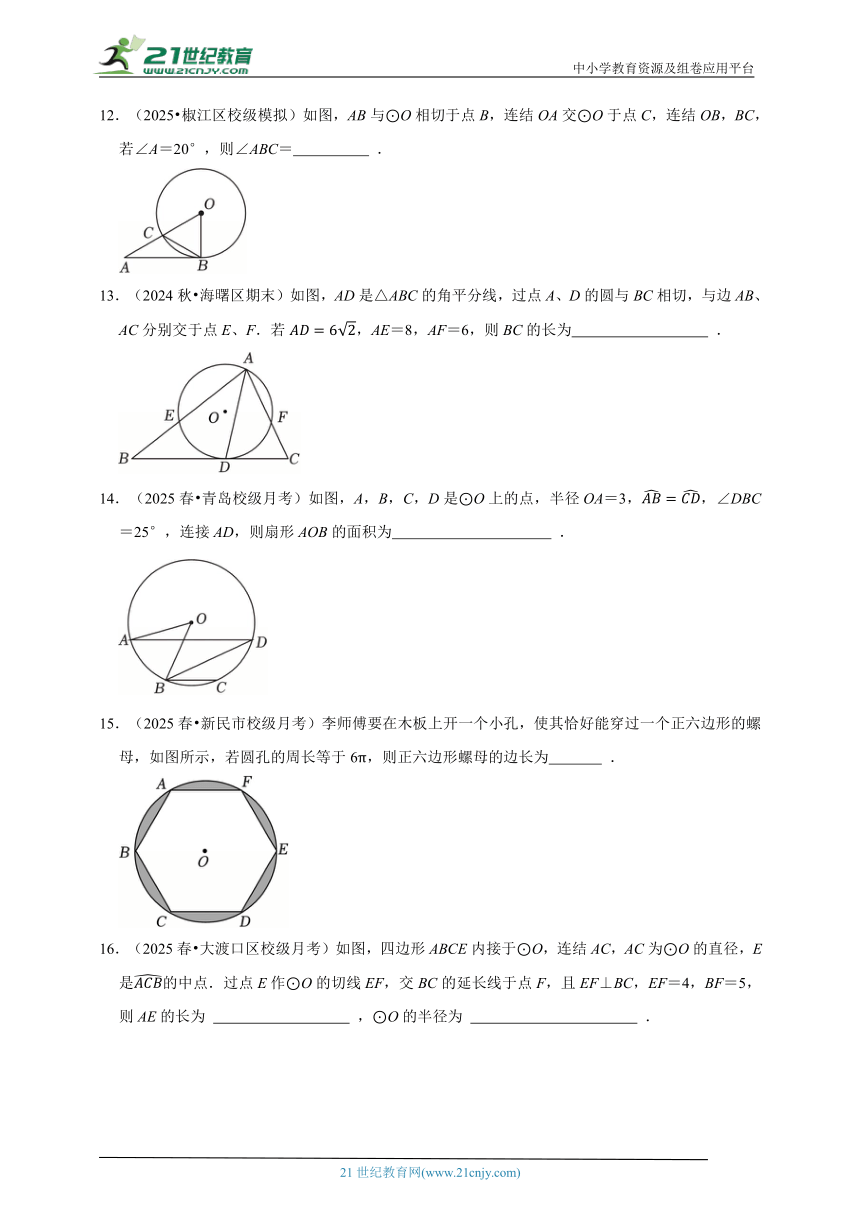
12.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= .
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 .
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
15.(2025春 新民市校级月考)李师傅要在木板上开一个小孔,使其恰好能穿过一个正六边形的螺母,如图所示,若圆孔的周长等于6π,则正六边形螺母的边长为 .
16.(2025春 大渡口区校级月考)如图,四边形ABCE内接于⊙O,连结AC,AC为⊙O的直径,E是的中点.过点E作⊙O的切线EF,交BC的延长线于点F,且EF⊥BC,EF=4,BF=5,则AE的长为 ,⊙O的半径为 .
17.(2025春 静安区校级月考)如图,直线AB与x轴、y轴分别相交于A、B两点,点A(﹣3,0),点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与线段AB有公共点时,令圆心P的横坐标为m,则m的取值范围是 .
三.解答题(共7小题)
18.(2025 太和县三模)如图,AB为⊙O的直径,C为BA延长线上一点,CE是⊙O的切线,过点B作BD⊥CE,交CE的延长线于点D,连接AE,BE.
(1)求证:BE平分∠CBD.
(2)若BE=10,⊙O的半径为6,求BD的长.
19.(2025春 西城区校级月考)如图,已知AB是⊙O的直径,点P在BA的延长线上,AB=BE,PD切⊙O于点D,交EB于点C,连接AE.
(1)求证:BE⊥PC;
(2)连接OC,BD交于点G,若AE=4,∠P=30°,求GC的长.
20.(2025 宜城市二模)已知AC为⊙O的直径,PA与⊙O相切于点A,弦BD⊥AC于点M,PA=PB.
(1)求证:PB为⊙O的切线;
(2)若∠P=60°,OM=2,求图中阴影部分图形的周长.
21.(2025 石家庄校级一模)如图1,某公园有一个圆形音乐喷泉,为了保障游客安全,管理部门打算在喷泉周围设置一圈防护栏现在对喷泉进行测量和规划,其示意图如图2所示,相关信息如下:
信息二:点O为喷泉中心,AB是喷泉边缘的一条弦,AB=8米,D是弦AB的中点,连接OD并延长,交劣弧AB于点C,CD=2米.
信息二:已知防护栏要距离喷泉边缘1米,以O为圆心,R为半径作防护栏所在圆.请根据以上信息解答下列问题:
(1)求喷泉的半径;
(2)要在防护栏上每隔1.5米安装一盏景观灯,大约需要安装多少盏景观灯?(π取3.14,结果保留整数)
22.(2025 天元区校级模拟)如图,在矩形ABCD中,O为边AB上一点,以点O为圆心,OA为半径的⊙O与对角线AC相交于点E,连接BE,且BC=BE.
(1)求证:BE是⊙O的切线;
(2)若∠CAB=30°,BC长为6,求⊙O的半径.
23.(2025 武汉模拟)菱形ABCD的顶点B,C,D在⊙O上,点O在线段AC上.
(1)如图1,若AB是⊙O的切线,求∠ADC的大小;
(2)如图2,若AB=2,AC=8,AB与⊙O交于点E.求BE的长.
24.(2025春 盖州市期中)在平面内对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形…
【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:如图2,如果六边形ABCDEF是等边半正六边形,那么AB=BC=CD=DE=EF=FA,∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B.
性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:
(1)等边半正六边形相邻两个内角的和为 .
(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想∠BAD与∠FAD的数量关系,并说明理由.
第2章对称图形-圆同步练习卷-数学九年级上册苏科版
参考答案与试题解析
一.选择题(共9小题)
题号 1 2 3 4 5 6 7 8 9
答案 C B B A D C A A B
一.选择题(共9小题)
1.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
【解答】解⊙O的半径为3,
点M到圆心O的距离为1.5,
∴OM<r,
∴点M在圆内.
故选:C.
2.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
【解答】解:∵圆锥的高OA=8,底面半径OB=6,
∴在Rt△AOB中,母线AB,
故选:B.
3.(2025春 鄞州区校级月考)一个圆锥的底面直径是8,母线长是7,则圆锥的侧面积是( )
A.16π B.28π C.42π D.56π
【解答】解:底面周长是8π,
则侧面积是:8π×7=28π.
故选:B.
4.(2024秋 滨江区期末)如图,线段AE是⊙O的直径,点B是⊙O上一点,设∠DAE=α,∠DCB=β.若AE⊥BC,BD=GD,则( )
A.3α+β=270° B.α+β=180° C.3β﹣α=270° D.β﹣α=90°
【解答】解:∵直径AB⊥BC,
∴,
∴∠ADB=∠ABC,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∵∠CDG+∠ADC=180°,
∴∠CDG=∠ABC,
∴∠CDG=ADB,
∵BD=CD,
∴∠G=DBG,
∴∠ADB=∠G+∠DBG=2∠G,
∵AB⊥BC,
∴∠G=90°﹣∠DAE=90°﹣α,
∴∠ADB=2(90°﹣α)=180°﹣2α,
∴∠CDG=180°﹣2α,
∴∠BCD=∠G+∠CDG=90°﹣α+180°﹣2α,
∴β=270°﹣3α,
∴3α+β=270°.
故选:A.
5.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
【解答】解:∵四边形ABCD内接于⊙O,
∴∠C+∠A=180°,
∵∠C=110°,
∴∠A=180°﹣110°=70°,
由圆周角定理得:∠BOD=2∠A=140°,
故选:D.
6.(2025春 琼海校级月考)如图,小珍同学借助直角三角板(∠ACB=60°)测量纸杯底面圆O的半径,圆O与边AC相切于点D,与BC的延长线相切于点E,测得CE=2cm,则底面圆O的半径为( )
A.2cm B. C. D.4cm
【解答】解:如图,连接OD、OE、OC,
∵∠ACB=60°,
∴∠ACE=120°,
∵CA、CE是圆O的切线,
∴OE⊥CE,∠OCE=∠OCD∠ACE=60°,
∴OE=CE tan∠OCE=2(cm),
故选:C.
7.(2025春 麒麟区校级月考)如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
【解答】解:如图,连接CD,
设∠ADB=x,
由条件可知AB=BC,∠O=∠ABC,
∴,
∴∠CDB=∠ADB=x,
∴∠ADC=∠CDB+∠ADB=2x,
由圆周角定理得:∠O=2∠ADC=4x,
∴∠ABC=4x,
由条件可知∠ABC+∠ADC=180°,
∴4x+2x=180°,
解得x=30°,
∴∠ADB=30°,
故选:A.
8.(2025 韶关模拟)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
【解答】解:有弧长公式可得:这段弯管中的长为,
故选:A.
9.(2025 衡阳模拟)如图,在⊙O中,BC是切线,切点是B,直线CO交⊙O于点D,A,点E为⊙O上的一点,连接BE,DE.若∠C=24°,则∠E的度数为( )
A.66° B.33° C.34° D.24°
【解答】解:如图所示,连接OB,
∵BC是⊙O的切线,切点是B,
∴∠OBC=90°,
∵在Rt△OBC中,∠C=24°,
∴∠BOD=90°﹣∠C=66°,
∵圆周角∠E与圆心角∠BOD所对的弧是BD,
∴.
故选:B.
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
【解答】解:由条件可知这条弦所对的圆心角的度数为,
∴这条弦与两条半径构成一个等腰直角三角形,
∴这条弦的长度为.
故答案为:.
11.(2025 徐州一模)已知一个正多边形的一个外角为20°,则它的边数是 18 .
【解答】解:由正多边形的外角和为360°,所以这个正多边形的边数为360÷20=18(条),
故答案为:18.
12.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= 35° .
【解答】解:∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=20°,
∴∠AOB=90°﹣20°=70°,
∵OB=OC,
∴∠OBC(180°﹣70°)=55°,
∴∠ABC=90°﹣55°=35°,
故答案为:35°.
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 7 .
【解答】解:如图,作圆O的直径DG,连接AG,
∴∠DAG=90°,
∴∠DAE+∠EAG=90°,
∵BC是⊙O的切线,
∴∠GDB=90°,
∴∠EDB+∠EDG=90°,
∵∠EAG=∠EDG,
∴∠EDB=∠DAE,
同理∠FDC=∠DAF,
连接DE,DF,
∵AD是△ABC的角平分线,
∴∠DAB=∠DAC,
∴∠CDF=∠EDB=∠DAC=∠EAD,
∴∠ADB=∠ADE+∠BDE=∠AFD,
∴△ADB∽△AFD,
∴,
∴6AB=(6)2,
∴AB=12,
∴BE=AB﹣AE=12﹣8=4,
∵∠B=∠B,∠BDE=∠EAD,
∴△EDB∽△DAB,
∴,
∴BD2=BE AB=4×12=48,
∴BD=4,
∵△ADB∽△AFD,
∴,
∴12DF=46,
∴DF=2,
∵∠CFD=∠AED,∠CDF=∠EAD,
∴△CDF∽△DAE,
∴,
∴,
∴CD=3,
∴BC=BD+CD=437.
故答案为:7.
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
【解答】解:如图,连接AC,
则∠DAC=∠DBC=25°,
∵,
∴∠ADB=∠DAC=25°,
∴∠AOB=2∠ADB=50°,
∵OA=3,
∴扇形AOB的面积为,
故答案为:
15.(2025春 新民市校级月考)李师傅要在木板上开一个小孔,使其恰好能穿过一个正六边形的螺母,如图所示,若圆孔的周长等于6π,则正六边形螺母的边长为 3 .
【解答】解:如图,连接OC、OD,
∵圆孔的周长等于6π,
∴圆孔的半径OC=6π÷2π=3,
∵六边形ABCDEF为正六边形,
∴∠COD60°,
∵OC=OD,
∴△COD为等边三角形,
∴CD=OC=3,
∴正六边形螺母的边长为3,
故答案为:3.
16.(2025春 大渡口区校级月考)如图,四边形ABCE内接于⊙O,连结AC,AC为⊙O的直径,E是的中点.过点E作⊙O的切线EF,交BC的延长线于点F,且EF⊥BC,EF=4,BF=5,则AE的长为 ,⊙O的半径为 .
【解答】解:如图,连接BE,
∵EF⊥BC,EF=4,BF=5,
∴BE,
∵E是的中点,
∴,
∴∠ABE=∠BAE,
∴AE=BE,
如图,过点E作EH⊥AC于H,连接OE,
∴∠EHA=∠EFB=90°,
又∵∠EAH=∠EBF,AE=BE,
∴△EAH≌△EBF(AAS),
∴AH=BF=5,EH=EF=4,
∵OE2=EH2+OH2,
∴OE2=16+(5﹣OE)2,
∴OE,
∴,⊙O的半径为,
故答案为:,.
17.(2025春 静安区校级月考)如图,直线AB与x轴、y轴分别相交于A、B两点,点A(﹣3,0),点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与线段AB有公共点时,令圆心P的横坐标为m,则m的取值范围是 ﹣4<m<﹣1 .
【解答】解:∵点A(﹣3,0),点,
∴,
∴,
∴∠BAO=30°,
当点P在点A右边,且⊙P与线段AB只有一个交点时,如图中P1:
∵⊙P与线段AB只有一个交点,
∴P1N⊥AB,
∴AP1=2P1N=2,
则P1(﹣1,0);
当点P在点A左边,且⊙P与线段AB只有一个交点时,如图中P2:
∵⊙P与线段AB只有一个交点,
∴⊙P与线段AB相交于点A,
∴P2A=1,A(﹣3,0),
则P2(﹣4,0);
综上:m的取值范围是﹣4<m<﹣1,
故答案为:﹣4<m<﹣1.
三.解答题(共7小题)
18.(2025 太和县三模)如图,AB为⊙O的直径,C为BA延长线上一点,CE是⊙O的切线,过点B作BD⊥CE,交CE的延长线于点D,连接AE,BE.
(1)求证:BE平分∠CBD.
(2)若BE=10,⊙O的半径为6,求BD的长.
【解答】(1)证明:如图,连接OE,
∵CE是⊙O的切线,
∴OE⊥CD,
∵BD⊥CE,
∴OE∥BD,
∴∠OEB=∠DBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠DEB,
∴BE平分∠CBD.
(2)解:∵AB为⊙O的直径,
∴∠BEA=90°,
∴∠BEA=∠BDE,
∵∠OBE=∠DEB,
∴△BDE∽△BEA,
∴,即,
解得:BD.
19.(2025春 西城区校级月考)如图,已知AB是⊙O的直径,点P在BA的延长线上,AB=BE,PD切⊙O于点D,交EB于点C,连接AE.
(1)求证:BE⊥PC;
(2)连接OC,BD交于点G,若AE=4,∠P=30°,求GC的长.
【解答】(1)证明:连接OD,BD,如图1所示:
∵AB是⊙O的直径,
∴∠ADB=90°,
即BD⊥AE,
∵AB=BE,
∴AD=ED,
∵OA=OB,
∴OD是△ABE的中位线,
∴OD∥BE,
∴AD与⊙O相切于点D,
∴OD⊥PC,
∴BE⊥PC;
(2)解:如图2所示:
∵AE=4,
由(1)得:AD=EDAE=2,
∵OD⊥PC,
∴△POD是直角三角形,
∵∠P=30°,
∴∠AOD=90°﹣∠P=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴OA=OD=AD=2,∠EAB=60°,
∵AB=BE,
∴△ABE是等边三角形,
∴AB=AE=BE=4,∠ABE=60°,
在Rt△ABE中,由勾股定理得:BD,
∵BD⊥AE,
∴∠DBC∠ABE=30°,
在RtBCD中,∠DBC=30°,
∴CDBD,
由勾股定理得:BC3,
在Rt△OCD中,由勾股定理得:OC,
∵OD∥BE,
∴△ODG∽△CBG,
∴,
设OG=2a,CG=3a,
∴OC=OG+CG=5a,
∴,
∴CG=3a.
20.(2025 宜城市二模)已知AC为⊙O的直径,PA与⊙O相切于点A,弦BD⊥AC于点M,PA=PB.
(1)求证:PB为⊙O的切线;
(2)若∠P=60°,OM=2,求图中阴影部分图形的周长.
【解答】(1)证明:连接OB、OP,
由条件可知OA⊥AP,
∴∠OAP=90°,
在△OBP和△OAP中,
,
∴△OBP≌△OAP(SSS),
∴∠OBP=∠OAP=90°,
∴OB⊥BP,
∴PB为⊙O的切线;
(2)解:由(1)知,∠OBP=∠OAP=90°,
由条件可知∠AOB=360°﹣90°﹣90°﹣60°=120°,
∴∠BOC=60°,
∴,
∴∠OMB=90°,,
∴∠OBM=90°﹣60°=30°,
由条件可知OB=2OM=4,
∴,
∴,
在△CDM和△OBM中,
,
∴△CMD≌△OMB(ASA),
∴CD=OB=4,
∵,
∴图中阴影部分图形的周长.
21.(2025 石家庄校级一模)如图1,某公园有一个圆形音乐喷泉,为了保障游客安全,管理部门打算在喷泉周围设置一圈防护栏现在对喷泉进行测量和规划,其示意图如图2所示,相关信息如下:
信息二:点O为喷泉中心,AB是喷泉边缘的一条弦,AB=8米,D是弦AB的中点,连接OD并延长,交劣弧AB于点C,CD=2米.
信息二:已知防护栏要距离喷泉边缘1米,以O为圆心,R为半径作防护栏所在圆.请根据以上信息解答下列问题:
(1)求喷泉的半径;
(2)要在防护栏上每隔1.5米安装一盏景观灯,大约需要安装多少盏景观灯?(π取3.14,结果保留整数)
【解答】解:(1)连接OA,设喷泉的半径为r,则:OA=OC=r,
∴OD=OC﹣CD=r﹣2,
由条件可知OC平分弦AB,,
∴OC⊥AB,
∴OA2=AD2+OD2,
∴r2=42+(r﹣2)2,
∴r=5米;
答:喷泉的半径为5米;
(2)由题意得:R=6米,
2×6×3.14÷1.5≈25(盏);
答:大约需要安装25盏景观灯.
22.(2025 天元区校级模拟)如图,在矩形ABCD中,O为边AB上一点,以点O为圆心,OA为半径的⊙O与对角线AC相交于点E,连接BE,且BC=BE.
(1)求证:BE是⊙O的切线;
(2)若∠CAB=30°,BC长为6,求⊙O的半径.
【解答】(1)证明:连接OE,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵OA=OE,BE=BC,
∴∠EAO=∠AEO,∠CEB=∠ACB,
∴∠ACB+∠CAB=∠AEO+∠CEB=90°,
∴∠OEB=90°,
∵OE为⊙O的半径,
∴BE是⊙O的切线;
(2)解:∵∠CAB=30°,∠ABC=90°,
∴∠ACB=60°,
∵BC=BE,
∴△BCE为等边三角形,
∴∠CBE=60°,CB=BE=6,
∴∠OBE=30°,
∴,
∴OE=6,
即⊙O的半径为2.
23.(2025 武汉模拟)菱形ABCD的顶点B,C,D在⊙O上,点O在线段AC上.
(1)如图1,若AB是⊙O的切线,求∠ADC的大小;
(2)如图2,若AB=2,AC=8,AB与⊙O交于点E.求BE的长.
【解答】解:(1)如图1,连接OB、OD,则OD=OB,
∵AB是⊙O的切线,
∴AB⊥OB,
∵四边形ABCD是菱形,
∴AD=AB=CD,
在△AOD和△AOB中,
,
∴△AOD≌△AOB(SSS),
∴∠ADO=∠ABO=90°,
∴∠DAC+∠AOD=90°,
∵∠DAC=∠DCA,∠AOD=2∠DCA,
∴∠DCA+2∠DCA=90°,
∴∠DAC=∠DCA=30°,
∴∠ADC=180°﹣∠DAC﹣∠DCA=180°﹣30°﹣30°=120°,
∴∠ADC的度数为120°.
(2)如图2,连接BF、EF,作BG⊥AC于点G,则∠CGB=90°,
∵AB=CB=2,AC=8,
∴AG=CGAC=4,
∵CF是⊙O的直径,
∴∠CBF=90°,
∴cos∠BCF,
∴CF6,
∴AF=AC﹣CF=8﹣6=2,
∵∠AEF+∠BEF=180°,∠ACB+∠BEF=180°,
∴∠AEF=∠ACB,
∵∠FAE=∠BAC,
∴△AEF∽△ACB,
∴,
∴AE,
∴BE=AB﹣AE=2,
∴BE的长为.
24.(2025春 盖州市期中)在平面内对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形…
【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:如图2,如果六边形ABCDEF是等边半正六边形,那么AB=BC=CD=DE=EF=FA,∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B.
性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:
(1)等边半正六边形相邻两个内角的和为 240° .
(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想∠BAD与∠FAD的数量关系,并说明理由.
【解答】解:(1)∵∠A+∠B+∠C+∠D+∠E+∠F=(6﹣2)×180°=720°,而∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B,
∴3∠A+3∠B=720°,
∴∠A+∠B240°,
即等边半正六边形相邻两个内角的和为240°,
故答案为:240°;
(2)证明:∠BAD=∠FAD,理由如下:
如图,连接AC、AE,
∵六边形ABCDEF是等边半正六边形,
∴AB=BC=AF=EF,∠B=∠F,
∴△ABC≌△AFE(SAS),
∴∠BAC=∠FAE,AC=AE,
又∵CD=DE,AD=AD,
∴△ACD≌△AED(SSS),
∴∠CAD=∠EAD,
∴∠CAD+∠BAC=∠EAD+∠FAE,
即∠BAD=∠FAD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2章对称图形-圆同步练习卷-数学九年级上册苏科版
一.选择题(共9小题)
1.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
2.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
3.(2025春 鄞州区校级月考)一个圆锥的底面直径是8,母线长是7,则圆锥的侧面积是( )
A.16π B.28π C.42π D.56π
4.(2024秋 滨江区期末)如图,线段AE是⊙O的直径,点B是⊙O上一点,设∠DAE=α,∠DCB=β.若AE⊥BC,BD=GD,则( )
A.3α+β=270° B.α+β=180° C.3β﹣α=270° D.β﹣α=90°
5.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
6.(2025春 琼海校级月考)如图,小珍同学借助直角三角板(∠ACB=60°)测量纸杯底面圆O的半径,圆O与边AC相切于点D,与BC的延长线相切于点E,测得CE=2cm,则底面圆O的半径为( )
A.2cm B. C. D.4cm
7.(2025春 麒麟区校级月考)如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
8.(2025 韶关模拟)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
9.(2025 衡阳模拟)如图,在⊙O中,BC是切线,切点是B,直线CO交⊙O于点D,A,点E为⊙O上的一点,连接BE,DE.若∠C=24°,则∠E的度数为( )
A.66° B.33° C.34° D.24°
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
11.(2025 徐州一模)已知一个正多边形的一个外角为20°,则它的边数是 .
12.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= .
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 .
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
15.(2025春 新民市校级月考)李师傅要在木板上开一个小孔,使其恰好能穿过一个正六边形的螺母,如图所示,若圆孔的周长等于6π,则正六边形螺母的边长为 .
16.(2025春 大渡口区校级月考)如图,四边形ABCE内接于⊙O,连结AC,AC为⊙O的直径,E是的中点.过点E作⊙O的切线EF,交BC的延长线于点F,且EF⊥BC,EF=4,BF=5,则AE的长为 ,⊙O的半径为 .
17.(2025春 静安区校级月考)如图,直线AB与x轴、y轴分别相交于A、B两点,点A(﹣3,0),点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与线段AB有公共点时,令圆心P的横坐标为m,则m的取值范围是 .
三.解答题(共7小题)
18.(2025 太和县三模)如图,AB为⊙O的直径,C为BA延长线上一点,CE是⊙O的切线,过点B作BD⊥CE,交CE的延长线于点D,连接AE,BE.
(1)求证:BE平分∠CBD.
(2)若BE=10,⊙O的半径为6,求BD的长.
19.(2025春 西城区校级月考)如图,已知AB是⊙O的直径,点P在BA的延长线上,AB=BE,PD切⊙O于点D,交EB于点C,连接AE.
(1)求证:BE⊥PC;
(2)连接OC,BD交于点G,若AE=4,∠P=30°,求GC的长.
20.(2025 宜城市二模)已知AC为⊙O的直径,PA与⊙O相切于点A,弦BD⊥AC于点M,PA=PB.
(1)求证:PB为⊙O的切线;
(2)若∠P=60°,OM=2,求图中阴影部分图形的周长.
21.(2025 石家庄校级一模)如图1,某公园有一个圆形音乐喷泉,为了保障游客安全,管理部门打算在喷泉周围设置一圈防护栏现在对喷泉进行测量和规划,其示意图如图2所示,相关信息如下:
信息二:点O为喷泉中心,AB是喷泉边缘的一条弦,AB=8米,D是弦AB的中点,连接OD并延长,交劣弧AB于点C,CD=2米.
信息二:已知防护栏要距离喷泉边缘1米,以O为圆心,R为半径作防护栏所在圆.请根据以上信息解答下列问题:
(1)求喷泉的半径;
(2)要在防护栏上每隔1.5米安装一盏景观灯,大约需要安装多少盏景观灯?(π取3.14,结果保留整数)
22.(2025 天元区校级模拟)如图,在矩形ABCD中,O为边AB上一点,以点O为圆心,OA为半径的⊙O与对角线AC相交于点E,连接BE,且BC=BE.
(1)求证:BE是⊙O的切线;
(2)若∠CAB=30°,BC长为6,求⊙O的半径.
23.(2025 武汉模拟)菱形ABCD的顶点B,C,D在⊙O上,点O在线段AC上.
(1)如图1,若AB是⊙O的切线,求∠ADC的大小;
(2)如图2,若AB=2,AC=8,AB与⊙O交于点E.求BE的长.
24.(2025春 盖州市期中)在平面内对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形…
【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:如图2,如果六边形ABCDEF是等边半正六边形,那么AB=BC=CD=DE=EF=FA,∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B.
性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:
(1)等边半正六边形相邻两个内角的和为 .
(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想∠BAD与∠FAD的数量关系,并说明理由.
第2章对称图形-圆同步练习卷-数学九年级上册苏科版
参考答案与试题解析
一.选择题(共9小题)
题号 1 2 3 4 5 6 7 8 9
答案 C B B A D C A A B
一.选择题(共9小题)
1.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
【解答】解⊙O的半径为3,
点M到圆心O的距离为1.5,
∴OM<r,
∴点M在圆内.
故选:C.
2.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
【解答】解:∵圆锥的高OA=8,底面半径OB=6,
∴在Rt△AOB中,母线AB,
故选:B.
3.(2025春 鄞州区校级月考)一个圆锥的底面直径是8,母线长是7,则圆锥的侧面积是( )
A.16π B.28π C.42π D.56π
【解答】解:底面周长是8π,
则侧面积是:8π×7=28π.
故选:B.
4.(2024秋 滨江区期末)如图,线段AE是⊙O的直径,点B是⊙O上一点,设∠DAE=α,∠DCB=β.若AE⊥BC,BD=GD,则( )
A.3α+β=270° B.α+β=180° C.3β﹣α=270° D.β﹣α=90°
【解答】解:∵直径AB⊥BC,
∴,
∴∠ADB=∠ABC,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∵∠CDG+∠ADC=180°,
∴∠CDG=∠ABC,
∴∠CDG=ADB,
∵BD=CD,
∴∠G=DBG,
∴∠ADB=∠G+∠DBG=2∠G,
∵AB⊥BC,
∴∠G=90°﹣∠DAE=90°﹣α,
∴∠ADB=2(90°﹣α)=180°﹣2α,
∴∠CDG=180°﹣2α,
∴∠BCD=∠G+∠CDG=90°﹣α+180°﹣2α,
∴β=270°﹣3α,
∴3α+β=270°.
故选:A.
5.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
【解答】解:∵四边形ABCD内接于⊙O,
∴∠C+∠A=180°,
∵∠C=110°,
∴∠A=180°﹣110°=70°,
由圆周角定理得:∠BOD=2∠A=140°,
故选:D.
6.(2025春 琼海校级月考)如图,小珍同学借助直角三角板(∠ACB=60°)测量纸杯底面圆O的半径,圆O与边AC相切于点D,与BC的延长线相切于点E,测得CE=2cm,则底面圆O的半径为( )
A.2cm B. C. D.4cm
【解答】解:如图,连接OD、OE、OC,
∵∠ACB=60°,
∴∠ACE=120°,
∵CA、CE是圆O的切线,
∴OE⊥CE,∠OCE=∠OCD∠ACE=60°,
∴OE=CE tan∠OCE=2(cm),
故选:C.
7.(2025春 麒麟区校级月考)如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
【解答】解:如图,连接CD,
设∠ADB=x,
由条件可知AB=BC,∠O=∠ABC,
∴,
∴∠CDB=∠ADB=x,
∴∠ADC=∠CDB+∠ADB=2x,
由圆周角定理得:∠O=2∠ADC=4x,
∴∠ABC=4x,
由条件可知∠ABC+∠ADC=180°,
∴4x+2x=180°,
解得x=30°,
∴∠ADB=30°,
故选:A.
8.(2025 韶关模拟)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
【解答】解:有弧长公式可得:这段弯管中的长为,
故选:A.
9.(2025 衡阳模拟)如图,在⊙O中,BC是切线,切点是B,直线CO交⊙O于点D,A,点E为⊙O上的一点,连接BE,DE.若∠C=24°,则∠E的度数为( )
A.66° B.33° C.34° D.24°
【解答】解:如图所示,连接OB,
∵BC是⊙O的切线,切点是B,
∴∠OBC=90°,
∵在Rt△OBC中,∠C=24°,
∴∠BOD=90°﹣∠C=66°,
∵圆周角∠E与圆心角∠BOD所对的弧是BD,
∴.
故选:B.
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
【解答】解:由条件可知这条弦所对的圆心角的度数为,
∴这条弦与两条半径构成一个等腰直角三角形,
∴这条弦的长度为.
故答案为:.
11.(2025 徐州一模)已知一个正多边形的一个外角为20°,则它的边数是 18 .
【解答】解:由正多边形的外角和为360°,所以这个正多边形的边数为360÷20=18(条),
故答案为:18.
12.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= 35° .
【解答】解:∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=20°,
∴∠AOB=90°﹣20°=70°,
∵OB=OC,
∴∠OBC(180°﹣70°)=55°,
∴∠ABC=90°﹣55°=35°,
故答案为:35°.
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 7 .
【解答】解:如图,作圆O的直径DG,连接AG,
∴∠DAG=90°,
∴∠DAE+∠EAG=90°,
∵BC是⊙O的切线,
∴∠GDB=90°,
∴∠EDB+∠EDG=90°,
∵∠EAG=∠EDG,
∴∠EDB=∠DAE,
同理∠FDC=∠DAF,
连接DE,DF,
∵AD是△ABC的角平分线,
∴∠DAB=∠DAC,
∴∠CDF=∠EDB=∠DAC=∠EAD,
∴∠ADB=∠ADE+∠BDE=∠AFD,
∴△ADB∽△AFD,
∴,
∴6AB=(6)2,
∴AB=12,
∴BE=AB﹣AE=12﹣8=4,
∵∠B=∠B,∠BDE=∠EAD,
∴△EDB∽△DAB,
∴,
∴BD2=BE AB=4×12=48,
∴BD=4,
∵△ADB∽△AFD,
∴,
∴12DF=46,
∴DF=2,
∵∠CFD=∠AED,∠CDF=∠EAD,
∴△CDF∽△DAE,
∴,
∴,
∴CD=3,
∴BC=BD+CD=437.
故答案为:7.
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
【解答】解:如图,连接AC,
则∠DAC=∠DBC=25°,
∵,
∴∠ADB=∠DAC=25°,
∴∠AOB=2∠ADB=50°,
∵OA=3,
∴扇形AOB的面积为,
故答案为:
15.(2025春 新民市校级月考)李师傅要在木板上开一个小孔,使其恰好能穿过一个正六边形的螺母,如图所示,若圆孔的周长等于6π,则正六边形螺母的边长为 3 .
【解答】解:如图,连接OC、OD,
∵圆孔的周长等于6π,
∴圆孔的半径OC=6π÷2π=3,
∵六边形ABCDEF为正六边形,
∴∠COD60°,
∵OC=OD,
∴△COD为等边三角形,
∴CD=OC=3,
∴正六边形螺母的边长为3,
故答案为:3.
16.(2025春 大渡口区校级月考)如图,四边形ABCE内接于⊙O,连结AC,AC为⊙O的直径,E是的中点.过点E作⊙O的切线EF,交BC的延长线于点F,且EF⊥BC,EF=4,BF=5,则AE的长为 ,⊙O的半径为 .
【解答】解:如图,连接BE,
∵EF⊥BC,EF=4,BF=5,
∴BE,
∵E是的中点,
∴,
∴∠ABE=∠BAE,
∴AE=BE,
如图,过点E作EH⊥AC于H,连接OE,
∴∠EHA=∠EFB=90°,
又∵∠EAH=∠EBF,AE=BE,
∴△EAH≌△EBF(AAS),
∴AH=BF=5,EH=EF=4,
∵OE2=EH2+OH2,
∴OE2=16+(5﹣OE)2,
∴OE,
∴,⊙O的半径为,
故答案为:,.
17.(2025春 静安区校级月考)如图,直线AB与x轴、y轴分别相交于A、B两点,点A(﹣3,0),点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与线段AB有公共点时,令圆心P的横坐标为m,则m的取值范围是 ﹣4<m<﹣1 .
【解答】解:∵点A(﹣3,0),点,
∴,
∴,
∴∠BAO=30°,
当点P在点A右边,且⊙P与线段AB只有一个交点时,如图中P1:
∵⊙P与线段AB只有一个交点,
∴P1N⊥AB,
∴AP1=2P1N=2,
则P1(﹣1,0);
当点P在点A左边,且⊙P与线段AB只有一个交点时,如图中P2:
∵⊙P与线段AB只有一个交点,
∴⊙P与线段AB相交于点A,
∴P2A=1,A(﹣3,0),
则P2(﹣4,0);
综上:m的取值范围是﹣4<m<﹣1,
故答案为:﹣4<m<﹣1.
三.解答题(共7小题)
18.(2025 太和县三模)如图,AB为⊙O的直径,C为BA延长线上一点,CE是⊙O的切线,过点B作BD⊥CE,交CE的延长线于点D,连接AE,BE.
(1)求证:BE平分∠CBD.
(2)若BE=10,⊙O的半径为6,求BD的长.
【解答】(1)证明:如图,连接OE,
∵CE是⊙O的切线,
∴OE⊥CD,
∵BD⊥CE,
∴OE∥BD,
∴∠OEB=∠DBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠DEB,
∴BE平分∠CBD.
(2)解:∵AB为⊙O的直径,
∴∠BEA=90°,
∴∠BEA=∠BDE,
∵∠OBE=∠DEB,
∴△BDE∽△BEA,
∴,即,
解得:BD.
19.(2025春 西城区校级月考)如图,已知AB是⊙O的直径,点P在BA的延长线上,AB=BE,PD切⊙O于点D,交EB于点C,连接AE.
(1)求证:BE⊥PC;
(2)连接OC,BD交于点G,若AE=4,∠P=30°,求GC的长.
【解答】(1)证明:连接OD,BD,如图1所示:
∵AB是⊙O的直径,
∴∠ADB=90°,
即BD⊥AE,
∵AB=BE,
∴AD=ED,
∵OA=OB,
∴OD是△ABE的中位线,
∴OD∥BE,
∴AD与⊙O相切于点D,
∴OD⊥PC,
∴BE⊥PC;
(2)解:如图2所示:
∵AE=4,
由(1)得:AD=EDAE=2,
∵OD⊥PC,
∴△POD是直角三角形,
∵∠P=30°,
∴∠AOD=90°﹣∠P=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴OA=OD=AD=2,∠EAB=60°,
∵AB=BE,
∴△ABE是等边三角形,
∴AB=AE=BE=4,∠ABE=60°,
在Rt△ABE中,由勾股定理得:BD,
∵BD⊥AE,
∴∠DBC∠ABE=30°,
在RtBCD中,∠DBC=30°,
∴CDBD,
由勾股定理得:BC3,
在Rt△OCD中,由勾股定理得:OC,
∵OD∥BE,
∴△ODG∽△CBG,
∴,
设OG=2a,CG=3a,
∴OC=OG+CG=5a,
∴,
∴CG=3a.
20.(2025 宜城市二模)已知AC为⊙O的直径,PA与⊙O相切于点A,弦BD⊥AC于点M,PA=PB.
(1)求证:PB为⊙O的切线;
(2)若∠P=60°,OM=2,求图中阴影部分图形的周长.
【解答】(1)证明:连接OB、OP,
由条件可知OA⊥AP,
∴∠OAP=90°,
在△OBP和△OAP中,
,
∴△OBP≌△OAP(SSS),
∴∠OBP=∠OAP=90°,
∴OB⊥BP,
∴PB为⊙O的切线;
(2)解:由(1)知,∠OBP=∠OAP=90°,
由条件可知∠AOB=360°﹣90°﹣90°﹣60°=120°,
∴∠BOC=60°,
∴,
∴∠OMB=90°,,
∴∠OBM=90°﹣60°=30°,
由条件可知OB=2OM=4,
∴,
∴,
在△CDM和△OBM中,
,
∴△CMD≌△OMB(ASA),
∴CD=OB=4,
∵,
∴图中阴影部分图形的周长.
21.(2025 石家庄校级一模)如图1,某公园有一个圆形音乐喷泉,为了保障游客安全,管理部门打算在喷泉周围设置一圈防护栏现在对喷泉进行测量和规划,其示意图如图2所示,相关信息如下:
信息二:点O为喷泉中心,AB是喷泉边缘的一条弦,AB=8米,D是弦AB的中点,连接OD并延长,交劣弧AB于点C,CD=2米.
信息二:已知防护栏要距离喷泉边缘1米,以O为圆心,R为半径作防护栏所在圆.请根据以上信息解答下列问题:
(1)求喷泉的半径;
(2)要在防护栏上每隔1.5米安装一盏景观灯,大约需要安装多少盏景观灯?(π取3.14,结果保留整数)
【解答】解:(1)连接OA,设喷泉的半径为r,则:OA=OC=r,
∴OD=OC﹣CD=r﹣2,
由条件可知OC平分弦AB,,
∴OC⊥AB,
∴OA2=AD2+OD2,
∴r2=42+(r﹣2)2,
∴r=5米;
答:喷泉的半径为5米;
(2)由题意得:R=6米,
2×6×3.14÷1.5≈25(盏);
答:大约需要安装25盏景观灯.
22.(2025 天元区校级模拟)如图,在矩形ABCD中,O为边AB上一点,以点O为圆心,OA为半径的⊙O与对角线AC相交于点E,连接BE,且BC=BE.
(1)求证:BE是⊙O的切线;
(2)若∠CAB=30°,BC长为6,求⊙O的半径.
【解答】(1)证明:连接OE,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵OA=OE,BE=BC,
∴∠EAO=∠AEO,∠CEB=∠ACB,
∴∠ACB+∠CAB=∠AEO+∠CEB=90°,
∴∠OEB=90°,
∵OE为⊙O的半径,
∴BE是⊙O的切线;
(2)解:∵∠CAB=30°,∠ABC=90°,
∴∠ACB=60°,
∵BC=BE,
∴△BCE为等边三角形,
∴∠CBE=60°,CB=BE=6,
∴∠OBE=30°,
∴,
∴OE=6,
即⊙O的半径为2.
23.(2025 武汉模拟)菱形ABCD的顶点B,C,D在⊙O上,点O在线段AC上.
(1)如图1,若AB是⊙O的切线,求∠ADC的大小;
(2)如图2,若AB=2,AC=8,AB与⊙O交于点E.求BE的长.
【解答】解:(1)如图1,连接OB、OD,则OD=OB,
∵AB是⊙O的切线,
∴AB⊥OB,
∵四边形ABCD是菱形,
∴AD=AB=CD,
在△AOD和△AOB中,
,
∴△AOD≌△AOB(SSS),
∴∠ADO=∠ABO=90°,
∴∠DAC+∠AOD=90°,
∵∠DAC=∠DCA,∠AOD=2∠DCA,
∴∠DCA+2∠DCA=90°,
∴∠DAC=∠DCA=30°,
∴∠ADC=180°﹣∠DAC﹣∠DCA=180°﹣30°﹣30°=120°,
∴∠ADC的度数为120°.
(2)如图2,连接BF、EF,作BG⊥AC于点G,则∠CGB=90°,
∵AB=CB=2,AC=8,
∴AG=CGAC=4,
∵CF是⊙O的直径,
∴∠CBF=90°,
∴cos∠BCF,
∴CF6,
∴AF=AC﹣CF=8﹣6=2,
∵∠AEF+∠BEF=180°,∠ACB+∠BEF=180°,
∴∠AEF=∠ACB,
∵∠FAE=∠BAC,
∴△AEF∽△ACB,
∴,
∴AE,
∴BE=AB﹣AE=2,
∴BE的长为.
24.(2025春 盖州市期中)在平面内对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形…
【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:如图2,如果六边形ABCDEF是等边半正六边形,那么AB=BC=CD=DE=EF=FA,∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B.
性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:
(1)等边半正六边形相邻两个内角的和为 240° .
(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想∠BAD与∠FAD的数量关系,并说明理由.
【解答】解:(1)∵∠A+∠B+∠C+∠D+∠E+∠F=(6﹣2)×180°=720°,而∠A=∠C=∠E,∠B=∠D=∠F,且∠A≠∠B,
∴3∠A+3∠B=720°,
∴∠A+∠B240°,
即等边半正六边形相邻两个内角的和为240°,
故答案为:240°;
(2)证明:∠BAD=∠FAD,理由如下:
如图,连接AC、AE,
∵六边形ABCDEF是等边半正六边形,
∴AB=BC=AF=EF,∠B=∠F,
∴△ABC≌△AFE(SAS),
∴∠BAC=∠FAE,AC=AE,
又∵CD=DE,AD=AD,
∴△ACD≌△AED(SSS),
∴∠CAD=∠EAD,
∴∠CAD+∠BAC=∠EAD+∠FAE,
即∠BAD=∠FAD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
