1.4一元一次不等式（二）

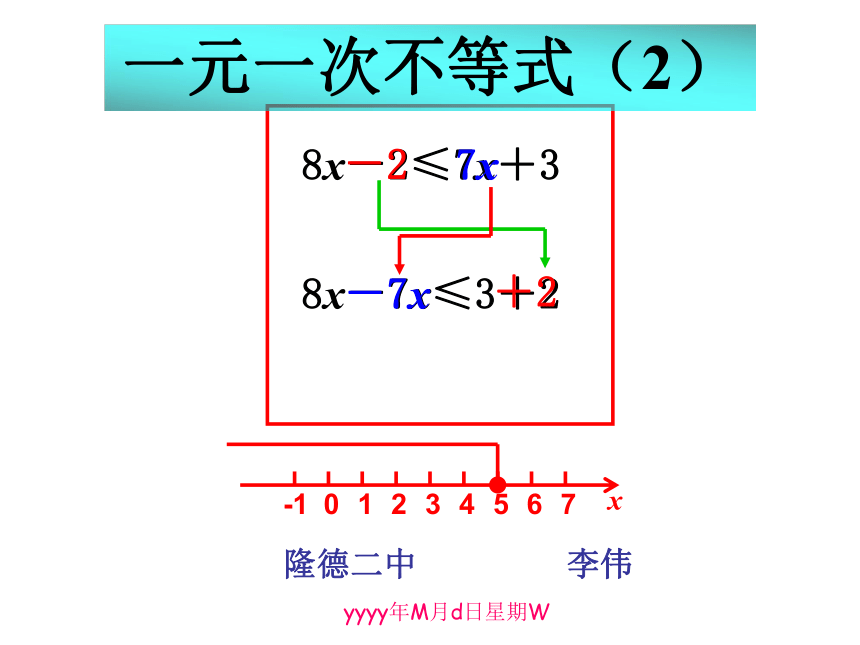
课件15张PPT。7x－7x－2＋2一元一次不等式（2）隆德二中 李伟2019年3月10日星期W一、复习旧知,方法归纳1、解下列不等式，并把它们的解集分别表示在数轴上2、求不等式4（x+1) ≤20的正整数解1.解一元一次不等式的一般步骤：
（1）去分母 等式性质2或3
注意：①勿漏乘不含分母的项；
②分子是两项或两项以上的代数式时要加括号；
③若两边同时乘以一个负数，须注意不等号的方向要改变.
去括号法则和分配律
注意：①勿漏乘括号内每一项；
②括号前面是“－”号，括号内各项要变号.移项法则（不等式性质1）
注意：移项要变号.合并同类项法则.
不等式基本性质2或性质3.
注意：两边同时除以未知数的系数时，要分清不等号的方向是否改变. (2)去括号（3）移项
（4）合并同类项
（5）系数化成1例1.某次知识竞赛共有25道题，答对一道题得4分，答错或不答一题扣1分。在这次竞赛中,小明被评为优秀(85分或85分以上)，小明至少要答对多少道题？4x(25-x)（２５－x）得分－扣分４x－(２５－x)８５或大于８５４x－(２５－x)≥８５二、合作探究，解决问题 解题过程４x－(２５－x)≥８５解这个不等式，得:X ≥ ２２共有2５道题，每答对一题得４分，答错或不答一题扣１分。小明得分要不少于８５分，他至少要答对多少道题？所以,小明至少答对了22道题.解：设小明答对x道题，则他答错或者不答
的题数为25－x，根据他的得分不少于８５分，
　得：
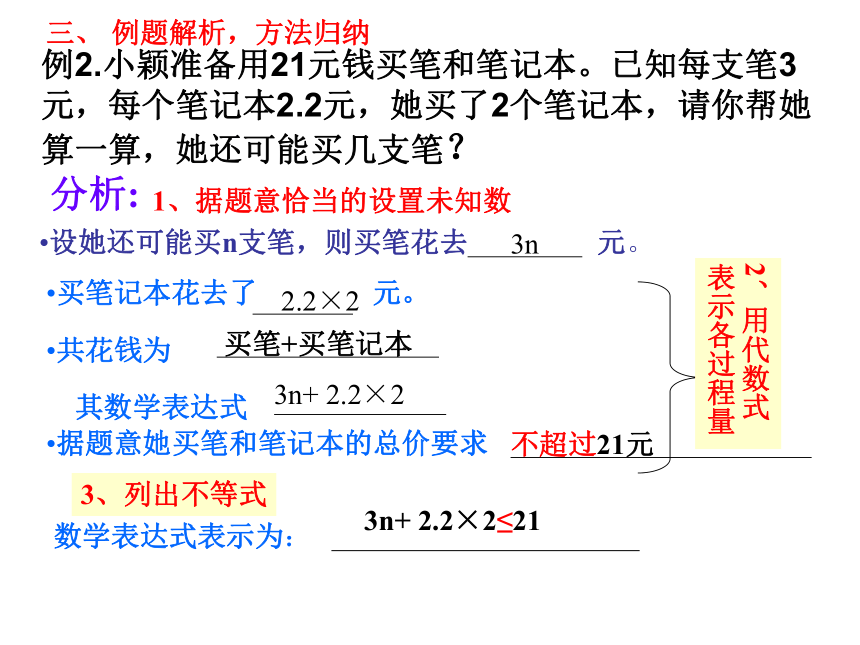
实际问题 抓关键语句解不等式，得出解答处理实际问题的一般方法2.表示过程的量1.设未知数3. 列不等式例2.小颖准备用21元钱买笔和笔记本。已知每支笔3元，每个笔记本2.2元，她买了2个笔记本，请你帮她算一算，她还可能买几支笔？3n2.2×2买笔+买笔记本3n+ 2.2×2不超过21元3n+ 2.2×2≤211、据题意恰当的设置未知数3、列出不等式分析:三、 例题解析，方法归纳例2. 小颖准备用21元钱买笔和笔记本。已知每枝笔3元，每个笔记本2.2元，她买了2个笔记本。请你帮她算一算，她还可能买几枝笔？解：设她还可能买n枝笔，根据题意，得3n+2.2×2≤21解这个不等式,得 : n≤因为在这一问题中n只能取正整数,
所以小颖还可能买1枝、2枝、3枝、4枝或5枝笔。注意: 问题的实际意义.解一元一次不等式应用题的步骤：（1）审题，找不等关系；
（2）设未知数；
（3）列不等式；
（4）解不等式；
（5）根据实际情况，写出全部答案
四、练习提高 2、小明准备用26元钱买火腿肠和方便面，已知一根火腿肠2元钱，一盒方便面3元钱，他买了5盒方便面，他还可能买多少根火腿肠？1、解下列不等式，并把它们的解集分别表示在数轴上： 5（x－ ) < 6x －小试牛刀2）小试牛刀 当x取何值时，代数式 的值比 的值大1？4）变式:当x取何值时，代数式 的值比 的值大于1？五、课堂小结通过本节课的学习，你有哪些收获？1、解一元一次不等式的一般步骤：
（1）去分母；
（2）去括号；
（3）移项；
（4）合并同类项；
（5）系数化成1.2、解一元一次不等式应用题的步骤：
（1）审题，找不等关系；
（2）设未知数；
（3）列不等式；
（4）解不等式；
（5）根据实际情况，写出全部答案作业1、课本P 18页1、2、3谢谢，再见！