第1单元长方体和正方体重难点检测卷(含答案)-数学六年级上册苏教版
文档属性
| 名称 | 第1单元长方体和正方体重难点检测卷(含答案)-数学六年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 641.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 15:00:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1单元长方体和正方体重难点检测卷-数学六年级上册苏教版
一.选择题(共8小题)
1.(2025 冷水滩区)制作一个长方体纸箱需要用多少纸板,这是求长方体的( )
A.体积 B.表面积 C.底面积 D.高
2.(2025春 房山区期末)一个骰子有六个面,每个面上分别到着1至6。如图两幅图是两次投掷后分别看到的情况,那么“1”的对面是( )
A.6 B.5 C.4 D.3
3.(2025 淅川县)由8个棱长是1cm的小正方体拼成的一个大正方体中拿走一个小正方体,这时它的表面积是( )cm2。
A.18 B.21 C.24 D.56
4.(2025 仙桃)如图中,甲的表面积与乙的表面积相比较,( )
A.甲大 B.乙大 C.一样大 D.无法确定
5.(2025 香洲区)一个长方体水箱,从里面量长6分米、宽4分米、高5分米,水箱中原有水的高度是3分米,放入一个体积为24立方分米的铁块(完全浸没)后,水上升的高度是( )
A.1分米 B.1.2分米 C.1.5分米 D.2分米
6.(2025 安定区)某学校科技小组仿照我国古代发明的水漏计时法,制作了一个长方体水漏计时器,该计时器长4分米、宽2分米、高3分米,加满水后全部漏完需6小时,一天中午12时,同学们往计时器里面加满水,当天下午4时,计时器里面还剩下( )升水。
A.24 B.4 C.8 D.16
7.(2025 七星关区)如图三种大小(单位:分米)的卡片各有2张,用这些卡片组成一个长方体,这个长方体的体积是( )立方分米。
A.30 B.50 C.60 D.90
8.(2025春 杭州期末)林林在一个长方体盒子中装了一些棱长为1分米的正方体,(如图)这个盒子的容积是( )
A.11立方分米 B.19立方分米
C.30立方分米 D.无法确定
二.填空题(共8小题)
9.(2025 鄂城区)把一根长24cm的铁丝折成一个最大的正方体框架,这个正方体的棱长是 cm,体积是 cm3。
10.(2025春 城关区期末)如图是一个底面是正方形的长方体以及这个长方体的侧面展开图。这个长方体的表面积是( )平方厘米。
11.(2025 清江浦区)一个长方体箱子的长、宽、高分别是16dm、12dm、10dm,在这个箱子里最多能放棱长为4dm的正方体 个。
12.(2024秋 淄博期末)把一根长6米,横截面是边长为2分米的正方形的长方体木料,平均截成了3段,表面积和比原来增加 平方分米,每段木料的体积是 立方分米。
13.(2025 济南)小明用一些棱长为1cm的正方体积木拼成了一个大长方体模型(如图)。它的表面积是 cm2,体积是 cm3。
14.(2025 邢台)如图,从长13cm、宽9cm的长方形硬纸板的四个角去掉边长为2cm的正方形后,沿虚线折叠成长方体纸盒,纸盒的容积是 cm3。
15.(2025 辽阳)一个棱长为4厘米的正方体,如果把它的棱长扩大到原来的2倍,那么它的表面积扩大到原来的 倍,体积扩大到原来的 倍。
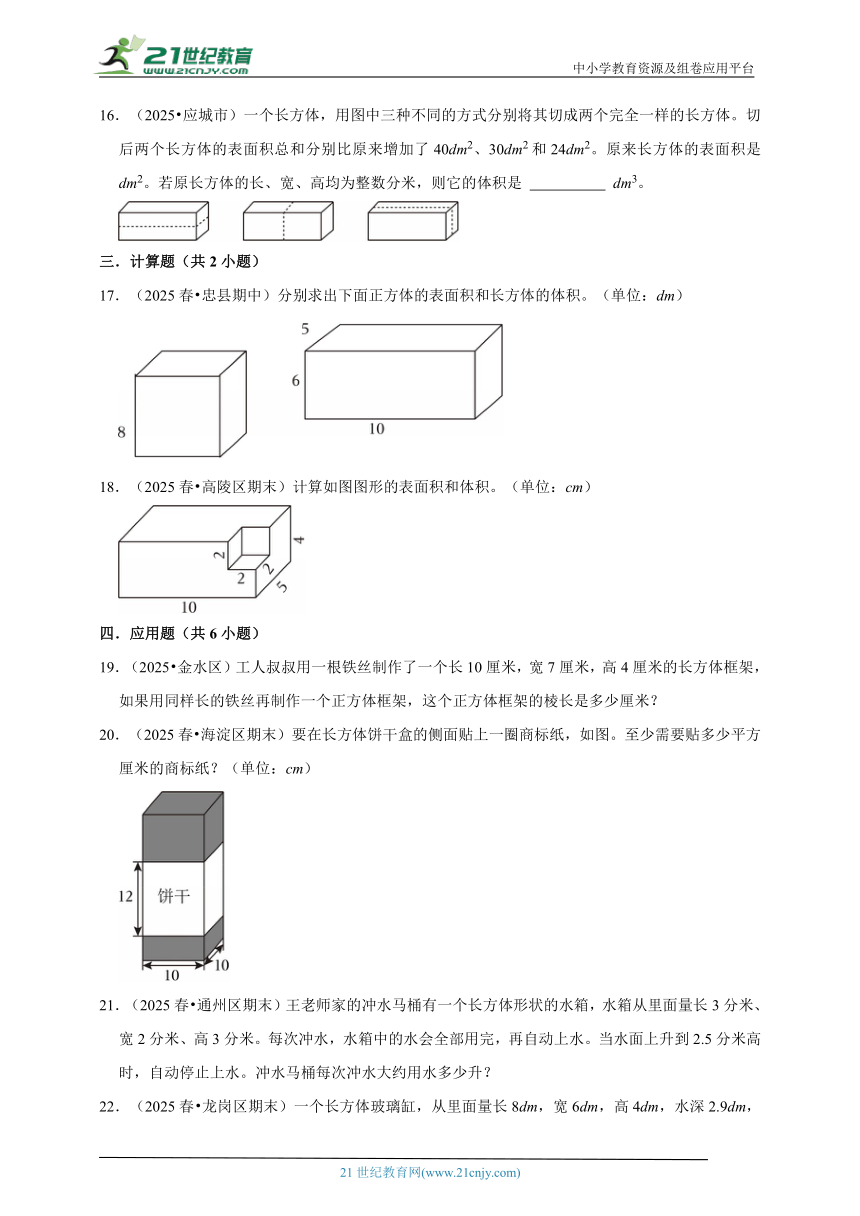
16.(2025 应城市)一个长方体,用图中三种不同的方式分别将其切成两个完全一样的长方体。切后两个长方体的表面积总和分别比原来增加了40dm2、30dm2和24dm2。原来长方体的表面积是 dm2。若原长方体的长、宽、高均为整数分米,则它的体积是 dm3。
三.计算题(共2小题)
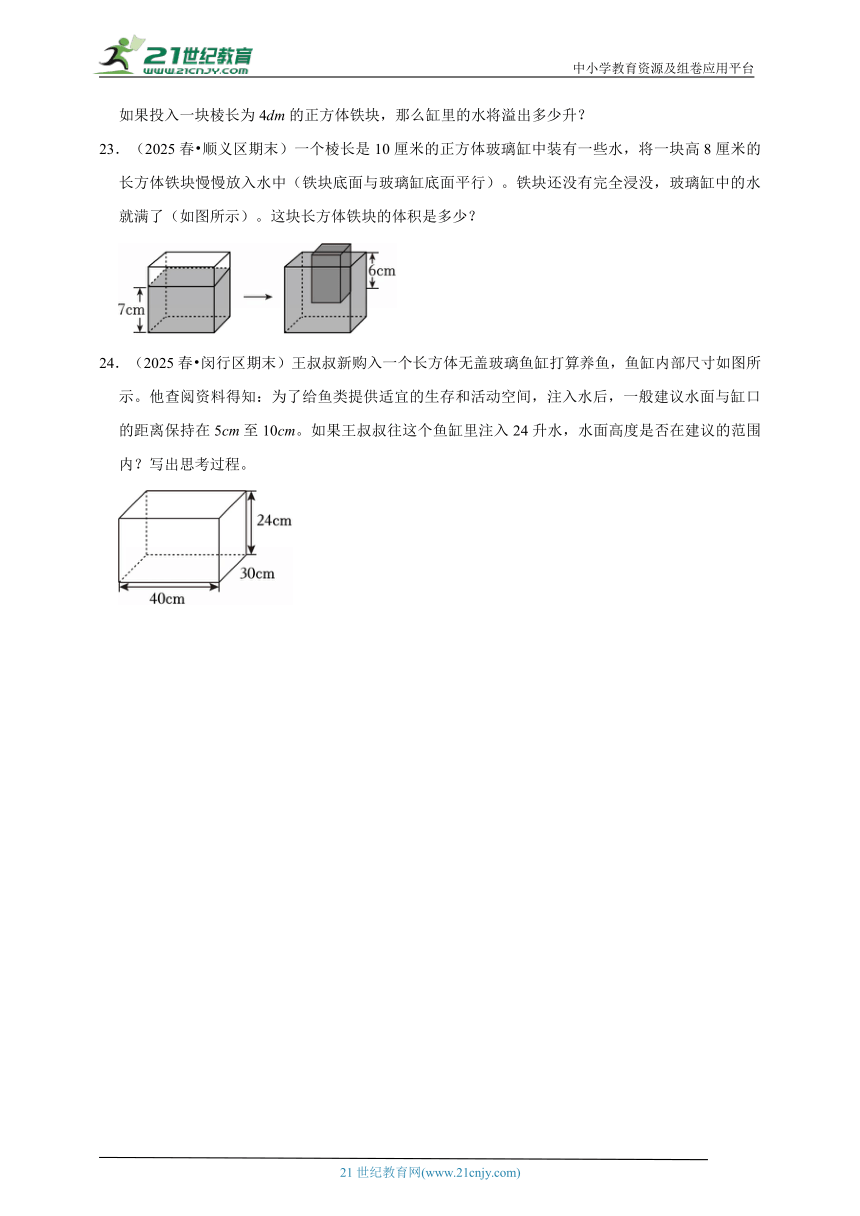
17.(2025春 忠县期中)分别求出下面正方体的表面积和长方体的体积。(单位:dm)
18.(2025春 高陵区期末)计算如图图形的表面积和体积。(单位:cm)
四.应用题(共6小题)
19.(2025 金水区)工人叔叔用一根铁丝制作了一个长10厘米,宽7厘米,高4厘米的长方体框架,如果用同样长的铁丝再制作一个正方体框架,这个正方体框架的棱长是多少厘米?
20.(2025春 海淀区期末)要在长方体饼干盒的侧面贴上一圈商标纸,如图。至少需要贴多少平方厘米的商标纸?(单位:cm)
21.(2025春 通州区期末)王老师家的冲水马桶有一个长方体形状的水箱,水箱从里面量长3分米、宽2分米、高3分米。每次冲水,水箱中的水会全部用完,再自动上水。当水面上升到2.5分米高时,自动停止上水。冲水马桶每次冲水大约用水多少升?
22.(2025春 龙岗区期末)一个长方体玻璃缸,从里面量长8dm,宽6dm,高4dm,水深2.9dm,如果投入一块棱长为4dm的正方体铁块,那么缸里的水将溢出多少升?
23.(2025春 顺义区期末)一个棱长是10厘米的正方体玻璃缸中装有一些水,将一块高8厘米的长方体铁块慢慢放入水中(铁块底面与玻璃缸底面平行)。铁块还没有完全浸没,玻璃缸中的水就满了(如图所示)。这块长方体铁块的体积是多少?
24.(2025春 闵行区期末)王叔叔新购入一个长方体无盖玻璃鱼缸打算养鱼,鱼缸内部尺寸如图所示。他查阅资料得知:为了给鱼类提供适宜的生存和活动空间,注入水后,一般建议水面与缸口的距离保持在5cm至10cm。如果王叔叔往这个鱼缸里注入24升水,水面高度是否在建议的范围内?写出思考过程。
第1单元长方体和正方体重难点检测卷-数学六年级上册苏教版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A C A A C A C
一.选择题(共8小题)
1.(2025 冷水滩区)制作一个长方体纸箱需要用多少纸板,这是求长方体的( )
A.体积 B.表面积 C.底面积 D.高
【解答】解:由分析得:制作一个长方体纸箱需要用多少纸板,这是求长方体的表面积。
故选:B。
2.(2025春 房山区期末)一个骰子有六个面,每个面上分别到着1至6。如图两幅图是两次投掷后分别看到的情况,那么“1”的对面是( )
A.6 B.5 C.4 D.3
【解答】解:第一次投掷后,1的对面不可能是1、2、3,则可能是4、5、6;第二次投掷后,1的对面不可能是1、4、5,则可能是2、3、6,结合两次可以得出“1”的对面是6。
故选:A。
3.(2025 淅川县)由8个棱长是1cm的小正方体拼成的一个大正方体中拿走一个小正方体,这时它的表面积是( )cm2。
A.18 B.21 C.24 D.56
【解答】解:2×2×6
=4×6
=24(平方厘米)
答:这时它的表面积是24平方厘米。
故选:C。
4.(2025 仙桃)如图中,甲的表面积与乙的表面积相比较,( )
A.甲大 B.乙大 C.一样大 D.无法确定
【解答】解:根据题干分析可得:正方体木块,挖去一个小正方体后,甲图在中间挖去,与原正方体的表面相比增加了两个小正方体的面,所以比原图形的表面积大;乙图在顶点上挖去,挖去小正方体后,其实剩下的图形的表面积与原图形的表面积是相等的。所以甲的表面积大于乙的表面积。
故选:A。
5.(2025 香洲区)一个长方体水箱,从里面量长6分米、宽4分米、高5分米,水箱中原有水的高度是3分米,放入一个体积为24立方分米的铁块(完全浸没)后,水上升的高度是( )
A.1分米 B.1.2分米 C.1.5分米 D.2分米
【解答】解:24÷(6×4)
=24÷24
=1(分米)
答:水上升的高度是1分米。
故选:A。
6.(2025 安定区)某学校科技小组仿照我国古代发明的水漏计时法,制作了一个长方体水漏计时器,该计时器长4分米、宽2分米、高3分米,加满水后全部漏完需6小时,一天中午12时,同学们往计时器里面加满水,当天下午4时,计时器里面还剩下( )升水。
A.24 B.4 C.8 D.16
【解答】解:4×2×3×(1﹣4÷6)
=24×(1)
=24
=8(立方分米)
8立方分米=升
答:计时器里面还剩下8升水。
故选:C。
7.(2025 七星关区)如图三种大小(单位:分米)的卡片各有2张,用这些卡片组成一个长方体,这个长方体的体积是( )立方分米。
A.30 B.50 C.60 D.90
【解答】解:5×2×3
=10×3
=30(立方分米)
答:这个长方体的体积是30立方分米。
故选:A。
8.(2025春 杭州期末)林林在一个长方体盒子中装了一些棱长为1分米的正方体,(如图)这个盒子的容积是( )
A.11立方分米 B.19立方分米
C.30立方分米 D.无法确定
【解答】解:5×3×2=30(立方分米)
答:这个盒子的容积是30立方分米。
故选:C。
二.填空题(共8小题)
9.(2025 鄂城区)把一根长24cm的铁丝折成一个最大的正方体框架,这个正方体的棱长是 2 cm,体积是 8 cm3。
【解答】解:24÷12=2(cm)
2×2×2
=4×2
=8(cm3)
答:这个正方体的棱长是2cm,体积是8cm3。
故答案为:2;8。
10.(2025春 城关区期末)如图是一个底面是正方形的长方体以及这个长方体的侧面展开图。这个长方体的表面积是( 434 )平方厘米。
【解答】解:长方体的长、宽:28÷4=7(厘米)
28×12+7×7×2
=336+98
=434(平方厘米)
答:这个长方体的表面积是434平方厘米。
故答案为:434。
11.(2025 清江浦区)一个长方体箱子的长、宽、高分别是16dm、12dm、10dm,在这个箱子里最多能放棱长为4dm的正方体 24 个。
【解答】解:16÷4=4(个)
12÷4=3(个)
10÷4=2(个)……2(dm)
4×3×2=24(个)
答:这个箱子最多能放24个棱长为4dm的正方体。
故答案为:24。
12.(2024秋 淄博期末)把一根长6米,横截面是边长为2分米的正方形的长方体木料,平均截成了3段,表面积和比原来增加 16 平方分米,每段木料的体积是 80 立方分米。
【解答】解:6米=60分米
2×2×4
=4×4
=16(平方分米)
2×2×(60÷3)
=4×20
=80(立方分米)
答:表面积比原来增加16平方分米,每段木料的体积是80立方分米。
故答案为:16,80。
13.(2025 济南)小明用一些棱长为1cm的正方体积木拼成了一个大长方体模型(如图)。它的表面积是 40 cm2,体积是 16 cm3。
【解答】解:(4×2+4×2+2×2)×2
=(8+8+4)×2
=20×2
=40(cm2)
4×2×2
=8×2
=16(cm3)
答:它的表面积是40cm2,体积是16cm3。
故答案为:40,16。
14.(2025 邢台)如图,从长13cm、宽9cm的长方形硬纸板的四个角去掉边长为2cm的正方形后,沿虚线折叠成长方体纸盒,纸盒的容积是 90 cm3。
【解答】解:(13﹣2﹣2)×(9﹣2﹣2)×2
=9×5×2
=90(立方厘米)
答:纸盒的容积是90立方厘米。
故答案为:90。
15.(2025 辽阳)一个棱长为4厘米的正方体,如果把它的棱长扩大到原来的2倍,那么它的表面积扩大到原来的 4 倍,体积扩大到原来的 8 倍。
【解答】解:2×2=4
2×2×2=8
答:它的表面积扩大到原来是4倍,体积扩大到原来的8倍。
故答案为:4,8。
16.(2025 应城市)一个长方体,用图中三种不同的方式分别将其切成两个完全一样的长方体。切后两个长方体的表面积总和分别比原来增加了40dm2、30dm2和24dm2。原来长方体的表面积是 94 dm2。若原长方体的长、宽、高均为整数分米,则它的体积是 120 dm3。
【解答】解:长方设体的长、宽、高分别为a分米、b分米、h分米。
则2ab=40平方分米,2bh=30平方分米,2ah=24平方分米,
40+30+24=94(平方分米)
(abh)2=(40×30×24)÷2
(abh)2=28800÷2
(abh)2=14400
abh=120
答:原来长方体的表面积是94平方分米,它的体积是120立方分米。
故答案为:94,120。
三.计算题(共2小题)
17.(2025春 忠县期中)分别求出下面正方体的表面积和长方体的体积。(单位:dm)
【解答】解:8×8×6
=64×6
=384(平方分米)
答:这个正方体的表面积是384平方分米。
(2)10×6×5
=60×5
=300(立方分米)
答:长方体的体积是300立方分米。
18.(2025春 高陵区期末)计算如图图形的表面积和体积。(单位:cm)
【解答】解:(10×5+10×4+5×4)×2
=(50+40+20)×2
=110×2
=220(平方厘米)
10×5×4﹣2×2×2
=200﹣8
=192(立方厘米)
答:组合体的表面积是220平方厘米,体积是192立方厘米。
四.应用题(共6小题)
19.(2025 金水区)工人叔叔用一根铁丝制作了一个长10厘米,宽7厘米,高4厘米的长方体框架,如果用同样长的铁丝再制作一个正方体框架,这个正方体框架的棱长是多少厘米?
【解答】解:(10+7+4)×4
=21×4
=84(厘米)
84÷12=7(厘米)
答:这个正方体框架的棱长是7厘米。
20.(2025春 海淀区期末)要在长方体饼干盒的侧面贴上一圈商标纸,如图。至少需要贴多少平方厘米的商标纸?(单位:cm)
【解答】解:10×12×4
=120×4
=480(平方厘米)
答:至少需要贴480平方厘米的商标纸。
21.(2025春 通州区期末)王老师家的冲水马桶有一个长方体形状的水箱,水箱从里面量长3分米、宽2分米、高3分米。每次冲水,水箱中的水会全部用完,再自动上水。当水面上升到2.5分米高时,自动停止上水。冲水马桶每次冲水大约用水多少升?
【解答】解:3×2×2.5
=6×2.5
=15(立方分米)
15立方分米=升
答:冲水马桶每次冲水大约用水15升。
22.(2025春 龙岗区期末)一个长方体玻璃缸,从里面量长8dm,宽6dm,高4dm,水深2.9dm,如果投入一块棱长为4dm的正方体铁块,那么缸里的水将溢出多少升?
【解答】解:4×4×4+8×6×2.9﹣8×6×4
=64+139.2﹣192
=11.2(立方分米)
11.2立方分米=11.2升
答:缸里的水将溢出11.2升。
23.(2025春 顺义区期末)一个棱长是10厘米的正方体玻璃缸中装有一些水,将一块高8厘米的长方体铁块慢慢放入水中(铁块底面与玻璃缸底面平行)。铁块还没有完全浸没,玻璃缸中的水就满了(如图所示)。这块长方体铁块的体积是多少?
【解答】解:10 7=3(厘米)
100×3=300(立方厘米)
300÷6=50(平方厘米)
50×8=400(立方厘米)
答:这块长方体铁块的体积是400立方厘米。
24.(2025春 闵行区期末)王叔叔新购入一个长方体无盖玻璃鱼缸打算养鱼,鱼缸内部尺寸如图所示。他查阅资料得知:为了给鱼类提供适宜的生存和活动空间,注入水后,一般建议水面与缸口的距离保持在5cm至10cm。如果王叔叔往这个鱼缸里注入24升水,水面高度是否在建议的范围内?写出思考过程。
【解答】解:24升=24立方分米=24000立方厘米
24000÷(40×30)
=24000÷1200
=20(厘米)
水面与缸口的距离:24﹣20=4(厘米),不在5厘米至10厘米范围内。
答:水面高度不在建议的范围内,注入24升水,水面高度是20厘米,水面与缸口的距离是4厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元长方体和正方体重难点检测卷-数学六年级上册苏教版
一.选择题(共8小题)
1.(2025 冷水滩区)制作一个长方体纸箱需要用多少纸板,这是求长方体的( )
A.体积 B.表面积 C.底面积 D.高
2.(2025春 房山区期末)一个骰子有六个面,每个面上分别到着1至6。如图两幅图是两次投掷后分别看到的情况,那么“1”的对面是( )
A.6 B.5 C.4 D.3
3.(2025 淅川县)由8个棱长是1cm的小正方体拼成的一个大正方体中拿走一个小正方体,这时它的表面积是( )cm2。
A.18 B.21 C.24 D.56
4.(2025 仙桃)如图中,甲的表面积与乙的表面积相比较,( )
A.甲大 B.乙大 C.一样大 D.无法确定
5.(2025 香洲区)一个长方体水箱,从里面量长6分米、宽4分米、高5分米,水箱中原有水的高度是3分米,放入一个体积为24立方分米的铁块(完全浸没)后,水上升的高度是( )
A.1分米 B.1.2分米 C.1.5分米 D.2分米
6.(2025 安定区)某学校科技小组仿照我国古代发明的水漏计时法,制作了一个长方体水漏计时器,该计时器长4分米、宽2分米、高3分米,加满水后全部漏完需6小时,一天中午12时,同学们往计时器里面加满水,当天下午4时,计时器里面还剩下( )升水。
A.24 B.4 C.8 D.16
7.(2025 七星关区)如图三种大小(单位:分米)的卡片各有2张,用这些卡片组成一个长方体,这个长方体的体积是( )立方分米。
A.30 B.50 C.60 D.90
8.(2025春 杭州期末)林林在一个长方体盒子中装了一些棱长为1分米的正方体,(如图)这个盒子的容积是( )
A.11立方分米 B.19立方分米
C.30立方分米 D.无法确定
二.填空题(共8小题)
9.(2025 鄂城区)把一根长24cm的铁丝折成一个最大的正方体框架,这个正方体的棱长是 cm,体积是 cm3。
10.(2025春 城关区期末)如图是一个底面是正方形的长方体以及这个长方体的侧面展开图。这个长方体的表面积是( )平方厘米。
11.(2025 清江浦区)一个长方体箱子的长、宽、高分别是16dm、12dm、10dm,在这个箱子里最多能放棱长为4dm的正方体 个。
12.(2024秋 淄博期末)把一根长6米,横截面是边长为2分米的正方形的长方体木料,平均截成了3段,表面积和比原来增加 平方分米,每段木料的体积是 立方分米。
13.(2025 济南)小明用一些棱长为1cm的正方体积木拼成了一个大长方体模型(如图)。它的表面积是 cm2,体积是 cm3。
14.(2025 邢台)如图,从长13cm、宽9cm的长方形硬纸板的四个角去掉边长为2cm的正方形后,沿虚线折叠成长方体纸盒,纸盒的容积是 cm3。
15.(2025 辽阳)一个棱长为4厘米的正方体,如果把它的棱长扩大到原来的2倍,那么它的表面积扩大到原来的 倍,体积扩大到原来的 倍。
16.(2025 应城市)一个长方体,用图中三种不同的方式分别将其切成两个完全一样的长方体。切后两个长方体的表面积总和分别比原来增加了40dm2、30dm2和24dm2。原来长方体的表面积是 dm2。若原长方体的长、宽、高均为整数分米,则它的体积是 dm3。
三.计算题(共2小题)
17.(2025春 忠县期中)分别求出下面正方体的表面积和长方体的体积。(单位:dm)
18.(2025春 高陵区期末)计算如图图形的表面积和体积。(单位:cm)
四.应用题(共6小题)
19.(2025 金水区)工人叔叔用一根铁丝制作了一个长10厘米,宽7厘米,高4厘米的长方体框架,如果用同样长的铁丝再制作一个正方体框架,这个正方体框架的棱长是多少厘米?
20.(2025春 海淀区期末)要在长方体饼干盒的侧面贴上一圈商标纸,如图。至少需要贴多少平方厘米的商标纸?(单位:cm)
21.(2025春 通州区期末)王老师家的冲水马桶有一个长方体形状的水箱,水箱从里面量长3分米、宽2分米、高3分米。每次冲水,水箱中的水会全部用完,再自动上水。当水面上升到2.5分米高时,自动停止上水。冲水马桶每次冲水大约用水多少升?
22.(2025春 龙岗区期末)一个长方体玻璃缸,从里面量长8dm,宽6dm,高4dm,水深2.9dm,如果投入一块棱长为4dm的正方体铁块,那么缸里的水将溢出多少升?
23.(2025春 顺义区期末)一个棱长是10厘米的正方体玻璃缸中装有一些水,将一块高8厘米的长方体铁块慢慢放入水中(铁块底面与玻璃缸底面平行)。铁块还没有完全浸没,玻璃缸中的水就满了(如图所示)。这块长方体铁块的体积是多少?
24.(2025春 闵行区期末)王叔叔新购入一个长方体无盖玻璃鱼缸打算养鱼,鱼缸内部尺寸如图所示。他查阅资料得知:为了给鱼类提供适宜的生存和活动空间,注入水后,一般建议水面与缸口的距离保持在5cm至10cm。如果王叔叔往这个鱼缸里注入24升水,水面高度是否在建议的范围内?写出思考过程。
第1单元长方体和正方体重难点检测卷-数学六年级上册苏教版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A C A A C A C
一.选择题(共8小题)
1.(2025 冷水滩区)制作一个长方体纸箱需要用多少纸板,这是求长方体的( )
A.体积 B.表面积 C.底面积 D.高
【解答】解:由分析得:制作一个长方体纸箱需要用多少纸板,这是求长方体的表面积。
故选:B。
2.(2025春 房山区期末)一个骰子有六个面,每个面上分别到着1至6。如图两幅图是两次投掷后分别看到的情况,那么“1”的对面是( )
A.6 B.5 C.4 D.3
【解答】解:第一次投掷后,1的对面不可能是1、2、3,则可能是4、5、6;第二次投掷后,1的对面不可能是1、4、5,则可能是2、3、6,结合两次可以得出“1”的对面是6。
故选:A。
3.(2025 淅川县)由8个棱长是1cm的小正方体拼成的一个大正方体中拿走一个小正方体,这时它的表面积是( )cm2。
A.18 B.21 C.24 D.56
【解答】解:2×2×6
=4×6
=24(平方厘米)
答:这时它的表面积是24平方厘米。
故选:C。
4.(2025 仙桃)如图中,甲的表面积与乙的表面积相比较,( )
A.甲大 B.乙大 C.一样大 D.无法确定
【解答】解:根据题干分析可得:正方体木块,挖去一个小正方体后,甲图在中间挖去,与原正方体的表面相比增加了两个小正方体的面,所以比原图形的表面积大;乙图在顶点上挖去,挖去小正方体后,其实剩下的图形的表面积与原图形的表面积是相等的。所以甲的表面积大于乙的表面积。
故选:A。
5.(2025 香洲区)一个长方体水箱,从里面量长6分米、宽4分米、高5分米,水箱中原有水的高度是3分米,放入一个体积为24立方分米的铁块(完全浸没)后,水上升的高度是( )
A.1分米 B.1.2分米 C.1.5分米 D.2分米
【解答】解:24÷(6×4)
=24÷24
=1(分米)
答:水上升的高度是1分米。
故选:A。
6.(2025 安定区)某学校科技小组仿照我国古代发明的水漏计时法,制作了一个长方体水漏计时器,该计时器长4分米、宽2分米、高3分米,加满水后全部漏完需6小时,一天中午12时,同学们往计时器里面加满水,当天下午4时,计时器里面还剩下( )升水。
A.24 B.4 C.8 D.16
【解答】解:4×2×3×(1﹣4÷6)
=24×(1)
=24
=8(立方分米)
8立方分米=升
答:计时器里面还剩下8升水。
故选:C。
7.(2025 七星关区)如图三种大小(单位:分米)的卡片各有2张,用这些卡片组成一个长方体,这个长方体的体积是( )立方分米。
A.30 B.50 C.60 D.90
【解答】解:5×2×3
=10×3
=30(立方分米)
答:这个长方体的体积是30立方分米。
故选:A。
8.(2025春 杭州期末)林林在一个长方体盒子中装了一些棱长为1分米的正方体,(如图)这个盒子的容积是( )
A.11立方分米 B.19立方分米
C.30立方分米 D.无法确定
【解答】解:5×3×2=30(立方分米)
答:这个盒子的容积是30立方分米。
故选:C。
二.填空题(共8小题)
9.(2025 鄂城区)把一根长24cm的铁丝折成一个最大的正方体框架,这个正方体的棱长是 2 cm,体积是 8 cm3。
【解答】解:24÷12=2(cm)
2×2×2
=4×2
=8(cm3)
答:这个正方体的棱长是2cm,体积是8cm3。
故答案为:2;8。
10.(2025春 城关区期末)如图是一个底面是正方形的长方体以及这个长方体的侧面展开图。这个长方体的表面积是( 434 )平方厘米。
【解答】解:长方体的长、宽:28÷4=7(厘米)
28×12+7×7×2
=336+98
=434(平方厘米)
答:这个长方体的表面积是434平方厘米。
故答案为:434。
11.(2025 清江浦区)一个长方体箱子的长、宽、高分别是16dm、12dm、10dm,在这个箱子里最多能放棱长为4dm的正方体 24 个。
【解答】解:16÷4=4(个)
12÷4=3(个)
10÷4=2(个)……2(dm)
4×3×2=24(个)
答:这个箱子最多能放24个棱长为4dm的正方体。
故答案为:24。
12.(2024秋 淄博期末)把一根长6米,横截面是边长为2分米的正方形的长方体木料,平均截成了3段,表面积和比原来增加 16 平方分米,每段木料的体积是 80 立方分米。
【解答】解:6米=60分米
2×2×4
=4×4
=16(平方分米)
2×2×(60÷3)
=4×20
=80(立方分米)
答:表面积比原来增加16平方分米,每段木料的体积是80立方分米。
故答案为:16,80。
13.(2025 济南)小明用一些棱长为1cm的正方体积木拼成了一个大长方体模型(如图)。它的表面积是 40 cm2,体积是 16 cm3。
【解答】解:(4×2+4×2+2×2)×2
=(8+8+4)×2
=20×2
=40(cm2)
4×2×2
=8×2
=16(cm3)
答:它的表面积是40cm2,体积是16cm3。
故答案为:40,16。
14.(2025 邢台)如图,从长13cm、宽9cm的长方形硬纸板的四个角去掉边长为2cm的正方形后,沿虚线折叠成长方体纸盒,纸盒的容积是 90 cm3。
【解答】解:(13﹣2﹣2)×(9﹣2﹣2)×2
=9×5×2
=90(立方厘米)
答:纸盒的容积是90立方厘米。
故答案为:90。
15.(2025 辽阳)一个棱长为4厘米的正方体,如果把它的棱长扩大到原来的2倍,那么它的表面积扩大到原来的 4 倍,体积扩大到原来的 8 倍。
【解答】解:2×2=4
2×2×2=8
答:它的表面积扩大到原来是4倍,体积扩大到原来的8倍。
故答案为:4,8。
16.(2025 应城市)一个长方体,用图中三种不同的方式分别将其切成两个完全一样的长方体。切后两个长方体的表面积总和分别比原来增加了40dm2、30dm2和24dm2。原来长方体的表面积是 94 dm2。若原长方体的长、宽、高均为整数分米,则它的体积是 120 dm3。
【解答】解:长方设体的长、宽、高分别为a分米、b分米、h分米。
则2ab=40平方分米,2bh=30平方分米,2ah=24平方分米,
40+30+24=94(平方分米)
(abh)2=(40×30×24)÷2
(abh)2=28800÷2
(abh)2=14400
abh=120
答:原来长方体的表面积是94平方分米,它的体积是120立方分米。
故答案为:94,120。
三.计算题(共2小题)
17.(2025春 忠县期中)分别求出下面正方体的表面积和长方体的体积。(单位:dm)
【解答】解:8×8×6
=64×6
=384(平方分米)
答:这个正方体的表面积是384平方分米。
(2)10×6×5
=60×5
=300(立方分米)
答:长方体的体积是300立方分米。
18.(2025春 高陵区期末)计算如图图形的表面积和体积。(单位:cm)
【解答】解:(10×5+10×4+5×4)×2
=(50+40+20)×2
=110×2
=220(平方厘米)
10×5×4﹣2×2×2
=200﹣8
=192(立方厘米)
答:组合体的表面积是220平方厘米,体积是192立方厘米。
四.应用题(共6小题)
19.(2025 金水区)工人叔叔用一根铁丝制作了一个长10厘米,宽7厘米,高4厘米的长方体框架,如果用同样长的铁丝再制作一个正方体框架,这个正方体框架的棱长是多少厘米?
【解答】解:(10+7+4)×4
=21×4
=84(厘米)
84÷12=7(厘米)
答:这个正方体框架的棱长是7厘米。
20.(2025春 海淀区期末)要在长方体饼干盒的侧面贴上一圈商标纸,如图。至少需要贴多少平方厘米的商标纸?(单位:cm)
【解答】解:10×12×4
=120×4
=480(平方厘米)
答:至少需要贴480平方厘米的商标纸。
21.(2025春 通州区期末)王老师家的冲水马桶有一个长方体形状的水箱,水箱从里面量长3分米、宽2分米、高3分米。每次冲水,水箱中的水会全部用完,再自动上水。当水面上升到2.5分米高时,自动停止上水。冲水马桶每次冲水大约用水多少升?
【解答】解:3×2×2.5
=6×2.5
=15(立方分米)
15立方分米=升
答:冲水马桶每次冲水大约用水15升。
22.(2025春 龙岗区期末)一个长方体玻璃缸,从里面量长8dm,宽6dm,高4dm,水深2.9dm,如果投入一块棱长为4dm的正方体铁块,那么缸里的水将溢出多少升?
【解答】解:4×4×4+8×6×2.9﹣8×6×4
=64+139.2﹣192
=11.2(立方分米)
11.2立方分米=11.2升
答:缸里的水将溢出11.2升。
23.(2025春 顺义区期末)一个棱长是10厘米的正方体玻璃缸中装有一些水,将一块高8厘米的长方体铁块慢慢放入水中(铁块底面与玻璃缸底面平行)。铁块还没有完全浸没,玻璃缸中的水就满了(如图所示)。这块长方体铁块的体积是多少?
【解答】解:10 7=3(厘米)
100×3=300(立方厘米)
300÷6=50(平方厘米)
50×8=400(立方厘米)
答:这块长方体铁块的体积是400立方厘米。
24.(2025春 闵行区期末)王叔叔新购入一个长方体无盖玻璃鱼缸打算养鱼,鱼缸内部尺寸如图所示。他查阅资料得知:为了给鱼类提供适宜的生存和活动空间,注入水后,一般建议水面与缸口的距离保持在5cm至10cm。如果王叔叔往这个鱼缸里注入24升水,水面高度是否在建议的范围内?写出思考过程。
【解答】解:24升=24立方分米=24000立方厘米
24000÷(40×30)
=24000÷1200
=20(厘米)
水面与缸口的距离:24﹣20=4(厘米),不在5厘米至10厘米范围内。
答:水面高度不在建议的范围内,注入24升水,水面高度是20厘米,水面与缸口的距离是4厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
