北京市西城区2015- 2016学年高一下学期期末考试数学试卷
文档属性
| 名称 | 北京市西城区2015- 2016学年高一下学期期末考试数学试卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 164.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-26 00:00:00 | ||
图片预览




文档简介
北京市西城区2015-2016学年下学期高一年级期末考试数学试卷
试卷满分:150分 考试时间:120分钟
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
1.已知数列满足,且,那么=( )
A. 8 B. 9 C. 10 D. 11
2. 如果,那么下列不等式正确的是( )
A. B. C. D.
3. 在掷一个骰子的试验中,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件发生的概率为( )
A. B. C. D.
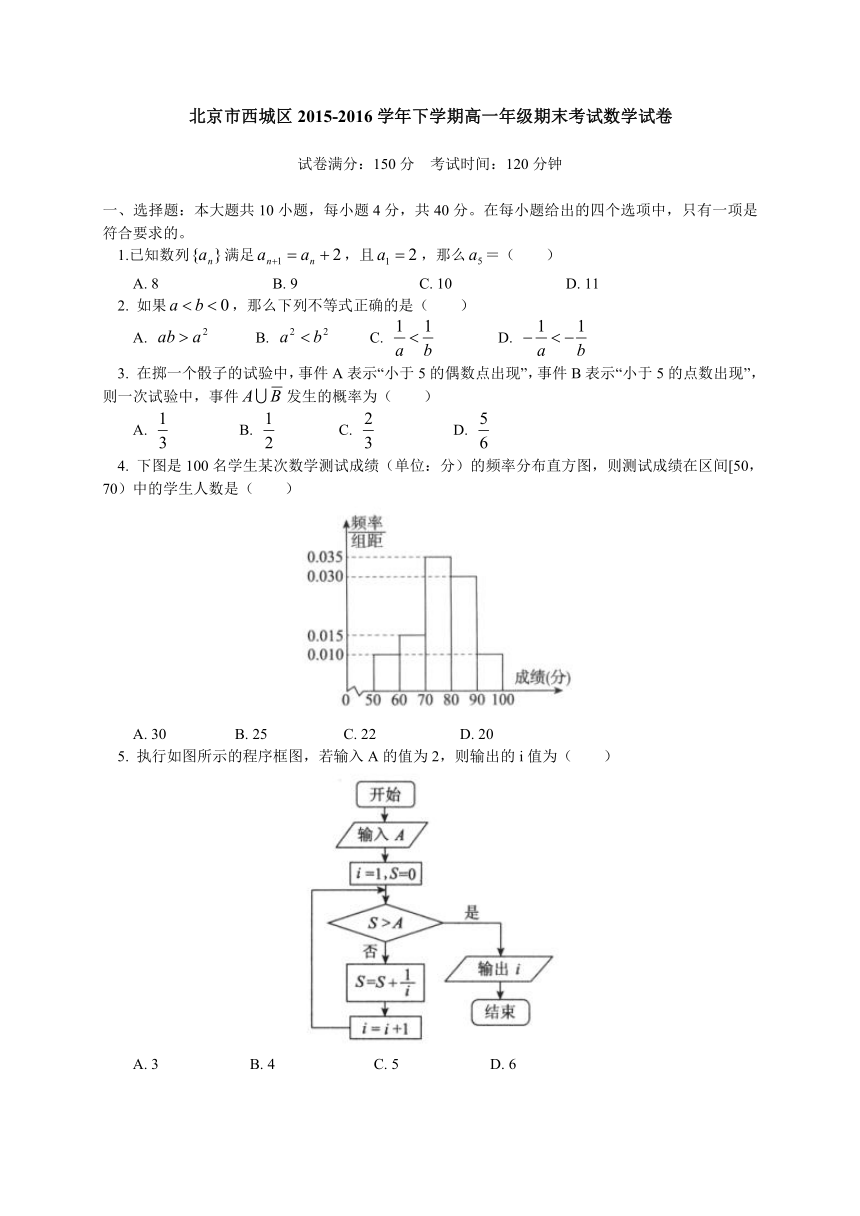
4. 下图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )
A. 30 B. 25 C. 22 D. 20
5. 执行如图所示的程序框图,若输入A的值为2,则输出的i值为( )
A. 3 B. 4 C. 5 D. 6
6. 在不等式组表示的平面区域内任取一个点,使得的概率为( )
A. B. C. D.
7. 若关于x的不等式对于一切恒成立,则实数a的取值范围是( )
A. B. C. D.
8. 在△ABC中,若,则△ABC为( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等边三角形
9. 某货运员拟运送甲、乙两种货物,每件货物的体积、重量、可获利润如下表所示:
体积(升/件)
重量(公斤/件)
利润(元/件)
甲
20
10
8
乙
10
20
10
在一次运输中,货物总体积不超过110升,总重量不超过100公斤,那么在合理的安排下,一次运输获得的最大利润为( )
A. 65元 B. 62元 C. 60元 D. 56元
10. 设,给出下列判断:
①若,则;
②若,则;
③若均为正数,且,则;
④若均为正数,且,则。
则所有正确判断的序号是( )
A. ①② B. ③ C. ③④ D. ②④
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上。
11. 不等式的解集为___________。
12. 下侧茎叶图记录了在某项体育比赛中,七位裁判为一名选手打出的分数,则去掉一个最高分和一个最低分后,所剩数据的平均值为___________,方差为__________。
13. 某学校举办了一次写作水平测试,成绩共有100分,85分,70分,60分及50分以下5种情况,并将成绩分成5个等级,从全校参赛学生中随机抽取30名学生,情况如下:
成绩等级
A
B
C
D
E
成绩(分)
100
85
70
60
50以下
人数(名)
1
a
b
8
c
已知在全校参加比赛的学生中任意抽取一人,估计出该同学成绩达到60分及60分以上的概率为,其成绩等级为“A或B”的概率为,则a=___________;b=__________。
14. 在各项均为正数的等比数列中,若,则的最小值是_________。
15. 某公司计划从五位大学毕业生甲、乙、丙、丁、戌中录用两人,若这五人被录用的机会均等,则甲或乙被录用的概率为__________。
16. 已知数列中,,.
①若,则a=__________;
②设是数列的前n项和,则=__________。
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分13分)
等差数列的首项,其前n项和为,且。
(Ⅰ)求的通项公式;
(Ⅱ)求满足不等式的n的值。
18. (本小题满分13分)
在△ABC中,角A,B,C的对边分别为,且。
(Ⅰ)若,求的值;
(Ⅱ)若△ABC的面积为,求c的值。
19. (本小题满分13分)
某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表。
组号
分组
频数
频率
第1组
[160,165)
5
0.050
第2组
[165,170)
①
0.350
第3组
[170,175)
30
②
第4组
[175,180)
20
0.200
第5组
[180,185]
10
0.100
合计
100
1.00
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,求第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅲ)在(Ⅱ)的前提下,学校决定在6
名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率。
20.(本小题满分13分)
已知函数。
(Ⅰ)当时,求在区间上的最大值和最小值;
(Ⅱ)解关于x的不等式;
(Ⅲ)当时,若存在,使得,求m的取值范围。
21.(本小题满分14分)
已知是递增的等差数列,为的前n项和,且成等比数列。
(Ⅰ)求数列的通项公式;
(Ⅱ)求的值;
(Ⅲ)若集合中有且仅有2个元素,求的取值范围。
22.(本小题满分14分)
已知数列的各项均为正数,其前n项和为,且满足。
(Ⅰ)若,求数列的通项公式;
(Ⅱ)若对于正整数这三项经过适当的排序后能构成等差数列,试用m表示和;
(Ⅲ)已知数列满足,数列的前100项和分别为,且,试问:是否对于任意的正整数均有成立,请说明理由。
【试题答案】
一、选择题:本大题共10小题,每小题4分,共40分。
1. C; 2. D; 3. C; 4. B; 5. C; 6. C; 7. B; 8. A; 9. B; 10. C。
二、填空题:本大题共6小题,每小题5分,共30分。
11. ; 12. 92,2.8; 13. 5,10;
14. ; 15. ; 16. 。
注:一题两空的题目,第一空2分,第二空3分。
三、解答题:本大题共6小题,共80分。
17. (本小题满分13分)
解:(Ⅰ)设数列的公差为d,
因为,所以。 3分
因为,所以,即, 5分
所以。 6分
(Ⅱ)因为,所以, 8分
由不等式,
得, 10分
所以,
解得, 12分
因为,
所以n的值为2,3,4。 13分
18.(本小题满分13分)
解:(Ⅰ)在△ABC中,, 3分
所以,
所以。 5分
(Ⅱ)因为, 7分
所以,
解得。 9分
又因为, 11分
所以,
所以。 13分
19. (本小题满分13分)
解:(Ⅰ)由题可知,第2组的频数为0.35×100=35人, ……………2分
第3组的频率为。 4分
所以①处的数据为35,②处的数据为0.300。 ……………5分
(Ⅱ)因为第3,4,5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组学生人数分别为:
第3组:人;第4组:人;第5组:人。
所以第3,4,5组分别抽取3人,2人,1人。 ……………8分
(注:第(Ⅰ)(Ⅱ)问仅写出正确答案,没有过程,各扣掉1分)
(Ⅲ)设第3组3位同学为A1,A2,A3,第4组2位同学为B1,B2,第5组1位同学为C1,
则从6位同学中抽两位同学的情况分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1)。
共有15种可能。 ……………10分
其中第4组的两位同学至少有一位同学被选中的情况分别为:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,C1),(B2,C1),(B1,B2)。
共有9种可能。 ……………12分
所以,第4组中至少有一名学生被抽中的概率为。
答:第4组中至少有一名学生被抽中的概率为。 ……………13分
20.(本小题满分13分)
解:(Ⅰ)当时,
函数在(-2,1)上是减函数,在(1,2)上是增函数。 2分
又,
所以,在区间上的最大值和最小值分别为4和-5。 4分
(Ⅱ)不等式,即,
当时,解得。 5分
当时,的两根为3和, 6分
当时,,不等式的解集为。 7分
当时,,
所以,当时,,不等式的解集为。 8分
当时,不等式的解集为。 9分
当时,,不等式的解集为。 10分
综上,当时,解集为;当时,解集为;当时,解集为;当时,解集为;当时,解集为。
(Ⅲ)因为,所以是开口向下的抛物线,
抛物线的对称轴为, 11分
若存在,使得,则, 12分
即,解得或,
综上,m的取值范围是。 13分
21.(本小题满分14分)
解:(Ⅰ)设等差数列的首项为,公差为d。
由,可得, 1分
由成等比数列,可得, 2分
所以
解得(舍)或 3分
所以数列的通项公式为。 4分
(Ⅱ)解可得,
所以数列中,其余各项均大于零。 6分
所以 7分
。 9分
(Ⅲ)设,
, 10分
令,得,
所以 11分
又由,知,其余各项均大于零。 12分
在中,,且 13分
计算得,
所以,的取值范围是。 14分
22.(本小题满分14分)
解:(Ⅰ)因为,
所以,,
所以,当时,, 2分
整理得,
又,所以=2,数列是公比为2的等比数列, 3分
所以数列的通项公式。 4分
(Ⅱ)由(Ⅰ)知,是公比为2的等比数列。
①若为的等差中项,则, 5分
所以,所以,
又,,所以,
所以。 7分
②若为的等差中项,则,
所以,所以,
所以,
等式左边为偶数,右边为奇数,等式不成立。 8分
③若为的等差中项,则,同理也不成立。
综上,。 9分
(Ⅲ)由,得,
所以或, 10分
若,不妨设,
则
。 11分
则
。 12分
由已知,所以,与已知不符,所以, 13分
所以,同上可得,
如此下去,,
即对于任意的正整数,均有。 14分
试卷满分:150分 考试时间:120分钟
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
1.已知数列满足,且,那么=( )
A. 8 B. 9 C. 10 D. 11
2. 如果,那么下列不等式正确的是( )
A. B. C. D.
3. 在掷一个骰子的试验中,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件发生的概率为( )
A. B. C. D.
4. 下图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )
A. 30 B. 25 C. 22 D. 20
5. 执行如图所示的程序框图,若输入A的值为2,则输出的i值为( )
A. 3 B. 4 C. 5 D. 6
6. 在不等式组表示的平面区域内任取一个点,使得的概率为( )
A. B. C. D.
7. 若关于x的不等式对于一切恒成立,则实数a的取值范围是( )
A. B. C. D.
8. 在△ABC中,若,则△ABC为( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等边三角形
9. 某货运员拟运送甲、乙两种货物,每件货物的体积、重量、可获利润如下表所示:
体积(升/件)
重量(公斤/件)
利润(元/件)
甲
20
10
8
乙
10
20
10
在一次运输中,货物总体积不超过110升,总重量不超过100公斤,那么在合理的安排下,一次运输获得的最大利润为( )
A. 65元 B. 62元 C. 60元 D. 56元
10. 设,给出下列判断:
①若,则;
②若,则;
③若均为正数,且,则;
④若均为正数,且,则。
则所有正确判断的序号是( )
A. ①② B. ③ C. ③④ D. ②④
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上。
11. 不等式的解集为___________。
12. 下侧茎叶图记录了在某项体育比赛中,七位裁判为一名选手打出的分数,则去掉一个最高分和一个最低分后,所剩数据的平均值为___________,方差为__________。
13. 某学校举办了一次写作水平测试,成绩共有100分,85分,70分,60分及50分以下5种情况,并将成绩分成5个等级,从全校参赛学生中随机抽取30名学生,情况如下:
成绩等级
A
B
C
D
E
成绩(分)
100
85
70
60
50以下
人数(名)
1
a
b
8
c
已知在全校参加比赛的学生中任意抽取一人,估计出该同学成绩达到60分及60分以上的概率为,其成绩等级为“A或B”的概率为,则a=___________;b=__________。
14. 在各项均为正数的等比数列中,若,则的最小值是_________。
15. 某公司计划从五位大学毕业生甲、乙、丙、丁、戌中录用两人,若这五人被录用的机会均等,则甲或乙被录用的概率为__________。
16. 已知数列中,,.
①若,则a=__________;
②设是数列的前n项和,则=__________。
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
17. (本小题满分13分)
等差数列的首项,其前n项和为,且。
(Ⅰ)求的通项公式;
(Ⅱ)求满足不等式的n的值。
18. (本小题满分13分)
在△ABC中,角A,B,C的对边分别为,且。
(Ⅰ)若,求的值;
(Ⅱ)若△ABC的面积为,求c的值。
19. (本小题满分13分)
某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表。
组号
分组
频数
频率
第1组
[160,165)
5
0.050
第2组
[165,170)
①
0.350
第3组
[170,175)
30
②
第4组
[175,180)
20
0.200
第5组
[180,185]
10
0.100
合计
100
1.00
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,求第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅲ)在(Ⅱ)的前提下,学校决定在6
名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率。
20.(本小题满分13分)
已知函数。
(Ⅰ)当时,求在区间上的最大值和最小值;
(Ⅱ)解关于x的不等式;
(Ⅲ)当时,若存在,使得,求m的取值范围。
21.(本小题满分14分)
已知是递增的等差数列,为的前n项和,且成等比数列。
(Ⅰ)求数列的通项公式;
(Ⅱ)求的值;
(Ⅲ)若集合中有且仅有2个元素,求的取值范围。
22.(本小题满分14分)
已知数列的各项均为正数,其前n项和为,且满足。
(Ⅰ)若,求数列的通项公式;
(Ⅱ)若对于正整数这三项经过适当的排序后能构成等差数列,试用m表示和;
(Ⅲ)已知数列满足,数列的前100项和分别为,且,试问:是否对于任意的正整数均有成立,请说明理由。
【试题答案】
一、选择题:本大题共10小题,每小题4分,共40分。
1. C; 2. D; 3. C; 4. B; 5. C; 6. C; 7. B; 8. A; 9. B; 10. C。
二、填空题:本大题共6小题,每小题5分,共30分。
11. ; 12. 92,2.8; 13. 5,10;
14. ; 15. ; 16. 。
注:一题两空的题目,第一空2分,第二空3分。
三、解答题:本大题共6小题,共80分。
17. (本小题满分13分)
解:(Ⅰ)设数列的公差为d,
因为,所以。 3分
因为,所以,即, 5分
所以。 6分
(Ⅱ)因为,所以, 8分
由不等式,
得, 10分
所以,
解得, 12分
因为,
所以n的值为2,3,4。 13分
18.(本小题满分13分)
解:(Ⅰ)在△ABC中,, 3分
所以,
所以。 5分
(Ⅱ)因为, 7分
所以,
解得。 9分
又因为, 11分
所以,
所以。 13分
19. (本小题满分13分)
解:(Ⅰ)由题可知,第2组的频数为0.35×100=35人, ……………2分
第3组的频率为。 4分
所以①处的数据为35,②处的数据为0.300。 ……………5分
(Ⅱ)因为第3,4,5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组学生人数分别为:
第3组:人;第4组:人;第5组:人。
所以第3,4,5组分别抽取3人,2人,1人。 ……………8分
(注:第(Ⅰ)(Ⅱ)问仅写出正确答案,没有过程,各扣掉1分)
(Ⅲ)设第3组3位同学为A1,A2,A3,第4组2位同学为B1,B2,第5组1位同学为C1,
则从6位同学中抽两位同学的情况分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1)。
共有15种可能。 ……………10分
其中第4组的两位同学至少有一位同学被选中的情况分别为:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,C1),(B2,C1),(B1,B2)。
共有9种可能。 ……………12分
所以,第4组中至少有一名学生被抽中的概率为。
答:第4组中至少有一名学生被抽中的概率为。 ……………13分
20.(本小题满分13分)
解:(Ⅰ)当时,
函数在(-2,1)上是减函数,在(1,2)上是增函数。 2分
又,
所以,在区间上的最大值和最小值分别为4和-5。 4分
(Ⅱ)不等式,即,
当时,解得。 5分
当时,的两根为3和, 6分
当时,,不等式的解集为。 7分
当时,,
所以,当时,,不等式的解集为。 8分
当时,不等式的解集为。 9分
当时,,不等式的解集为。 10分
综上,当时,解集为;当时,解集为;当时,解集为;当时,解集为;当时,解集为。
(Ⅲ)因为,所以是开口向下的抛物线,
抛物线的对称轴为, 11分
若存在,使得,则, 12分
即,解得或,
综上,m的取值范围是。 13分
21.(本小题满分14分)
解:(Ⅰ)设等差数列的首项为,公差为d。
由,可得, 1分
由成等比数列,可得, 2分
所以
解得(舍)或 3分
所以数列的通项公式为。 4分
(Ⅱ)解可得,
所以数列中,其余各项均大于零。 6分
所以 7分
。 9分
(Ⅲ)设,
, 10分
令,得,
所以 11分
又由,知,其余各项均大于零。 12分
在中,,且 13分
计算得,
所以,的取值范围是。 14分
22.(本小题满分14分)
解:(Ⅰ)因为,
所以,,
所以,当时,, 2分
整理得,
又,所以=2,数列是公比为2的等比数列, 3分
所以数列的通项公式。 4分
(Ⅱ)由(Ⅰ)知,是公比为2的等比数列。
①若为的等差中项,则, 5分
所以,所以,
又,,所以,
所以。 7分
②若为的等差中项,则,
所以,所以,
所以,
等式左边为偶数,右边为奇数,等式不成立。 8分
③若为的等差中项,则,同理也不成立。
综上,。 9分
(Ⅲ)由,得,
所以或, 10分
若,不妨设,
则
。 11分
则
。 12分
由已知,所以,与已知不符,所以, 13分
所以,同上可得,
如此下去,,
即对于任意的正整数,均有。 14分
同课章节目录
