第24章圆同步练习卷(含答案)-数学九年级上册人教版
文档属性
| 名称 | 第24章圆同步练习卷(含答案)-数学九年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 15:10:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第24章圆同步练习卷-数学九年级上册人教版
一.选择题(共9小题)
1.(2025春 浦东新区校级月考)下列命题正确的是( )
A.平分弦的查径垂直于弦
B.过三点可以确定一个圆
C.两圆的公共弦垂直平分连心线
D.等边三角形外接圆的面积是内切圆面积的4倍
2.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
3.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
4.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
5.(2025春 云岩区校级月考)如图,将△OAB绕着点O顺时针旋转60°后得到△OA′B′,若OB=5,则的长度为( )
A. B. C. D.
6.(2025春 榆树市校级月考)如图,点A、B、C在⊙O上,且AB=AC.若∠ABO=21°,则∠BOC的大小为( )
A.42° B.82° C.84° D.90°
7.(2025春 袁州区校级月考)如图,AB为⊙O的直径,点C在⊙O上,连接BC.若AB=2,BC=1,则阴影部分的面积为( )
A. B. C.π D.
8.(2025春 大渡口区校级月考)如图,△ABC内接于⊙O,AB为⊙O的直径,直线CD与⊙O相切于点C,过点O作OE∥BC,交CD于点E,若∠BAC=32°,则∠OEC的度数为( )
A.34° B.32° C.26° D.58°
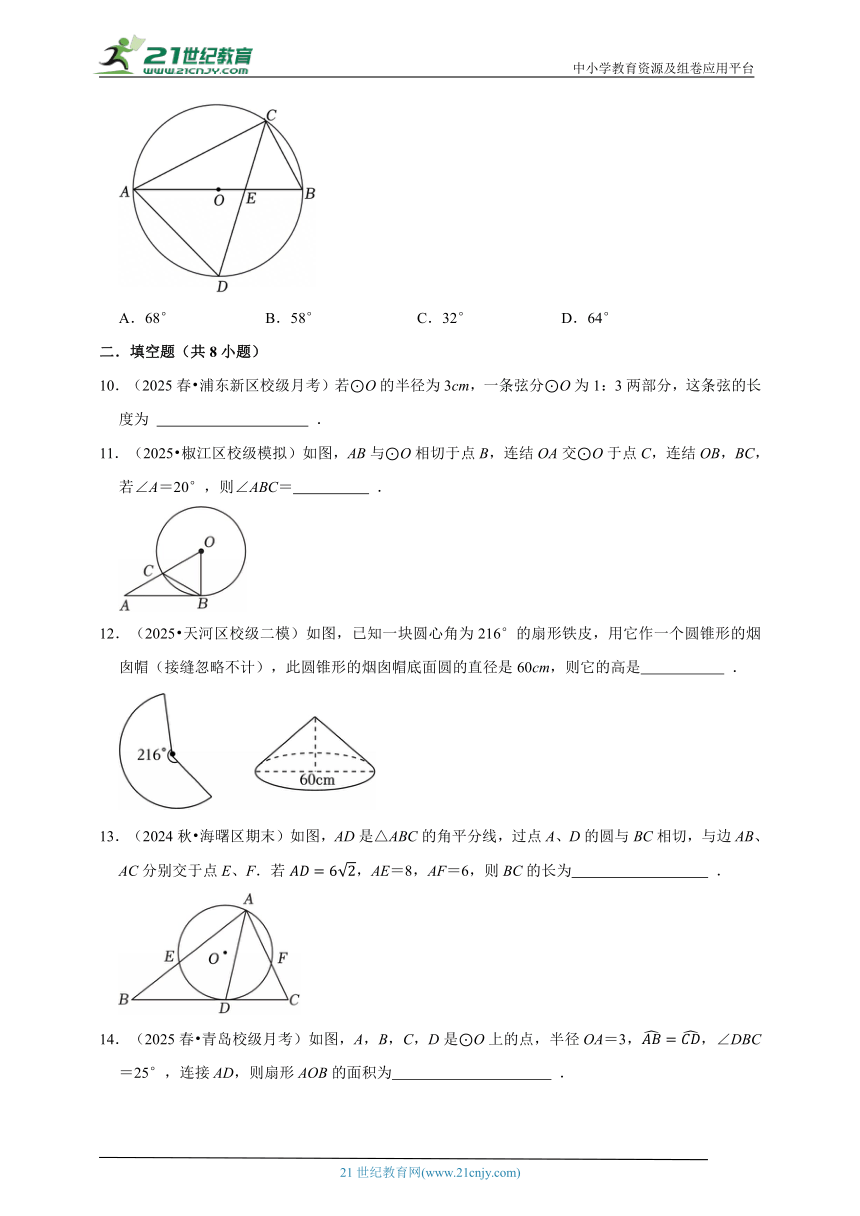
9.(2025 运城模拟)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD,BC.若∠BAC=32°,则∠D的度数为( )
A.68° B.58° C.32° D.64°
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
11.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= .
12.(2025 天河区校级二模)如图,已知一块圆心角为216°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),此圆锥形的烟囱帽底面圆的直径是60cm,则它的高是 .
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 .
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
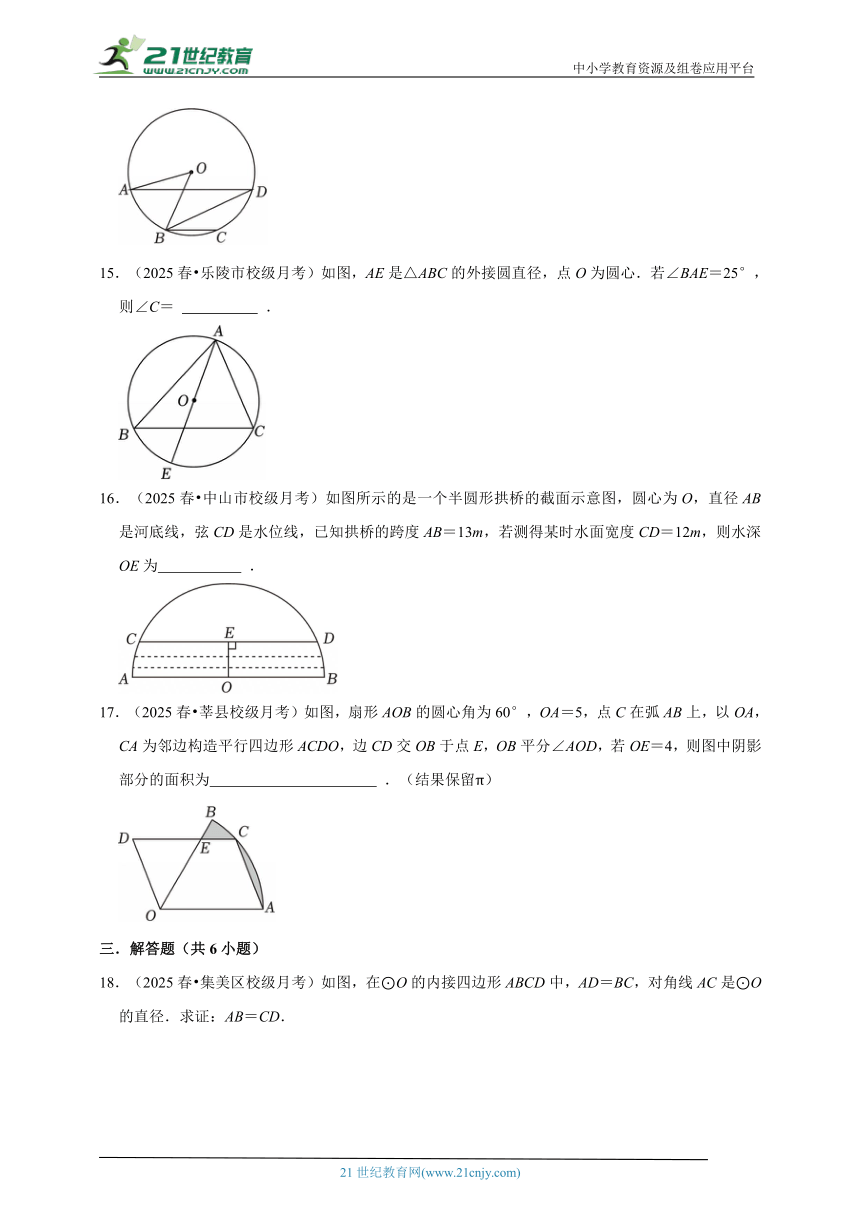
15.(2025春 乐陵市校级月考)如图,AE是△ABC的外接圆直径,点O为圆心.若∠BAE=25°,则∠C= .
16.(2025春 中山市校级月考)如图所示的是一个半圆形拱桥的截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,已知拱桥的跨度AB=13m,若测得某时水面宽度CD=12m,则水深OE为 .
17.(2025春 莘县校级月考)如图,扇形AOB的圆心角为60°,OA=5,点C在弧AB上,以OA,CA为邻边构造平行四边形ACDO,边CD交OB于点E,OB平分∠AOD,若OE=4,则图中阴影部分的面积为 .(结果保留π)
三.解答题(共6小题)
18.(2025春 集美区校级月考)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:AB=CD.
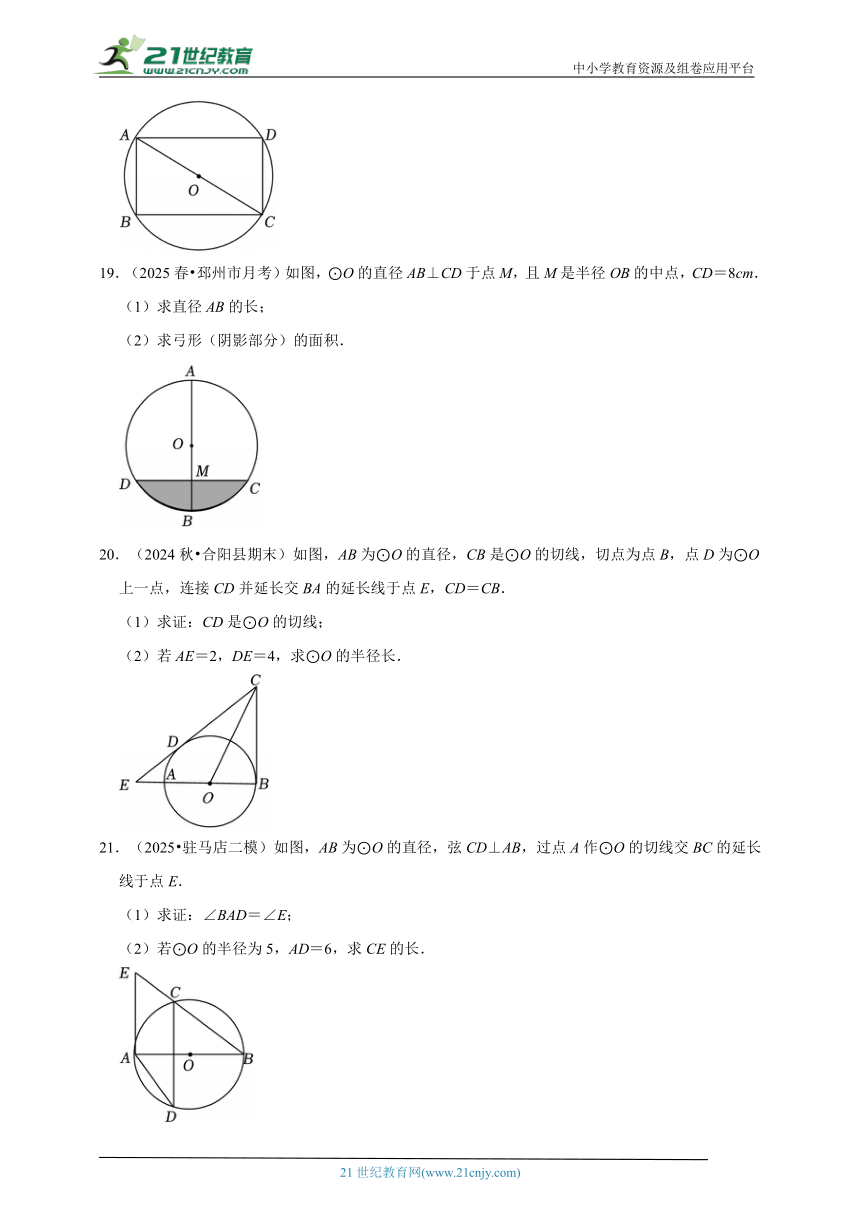
19.(2025春 邳州市月考)如图,⊙O的直径AB⊥CD于点M,且M是半径OB的中点,CD=8cm.
(1)求直径AB的长;
(2)求弓形(阴影部分)的面积.
20.(2024秋 合阳县期末)如图,AB为⊙O的直径,CB是⊙O的切线,切点为点B,点D为⊙O上一点,连接CD并延长交BA的延长线于点E,CD=CB.
(1)求证:CD是⊙O的切线;
(2)若AE=2,DE=4,求⊙O的半径长.
21.(2025 驻马店二模)如图,AB为⊙O的直径,弦CD⊥AB,过点A作⊙O的切线交BC的延长线于点E.
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AD=6,求CE的长.
22.(2025春 莘县校级月考)如图,△ABC内接于⊙O,BC是⊙O的直径,过点A作⊙O的切线交BC的延长线于点D,AE⊥BC于点F,交⊙O于点E.
(1)求证:∠DAE=2∠B;
(2)若CF=2OF,CD=12,求⊙O的半径.
23.(2025 新华区校级一模)如图1和图2,O为内、外两个圆的圆心,大圆被八等分,分点为A,B,C,D,E,F,G,H.已知两个圆的半径分别为1,3.
(1)如图1,若大圆中的弦AP与小圆相切于点M,求AP的长;
(2)通过计算比较弧AD的长和小圆的周长的大小;
(3)如图2,连接OB,AG,通过说理判断OB和AG的位置关系,并求点B到AG的距离.
第24章圆同步练习卷-数学九年级上册人教版
参考答案与试题解析
一.选择题(共9小题)
题号 1 2 3 4 5 6 7 8 9
答案 D C B D B C D B B
一.选择题(共9小题)
1.(2025春 浦东新区校级月考)下列命题正确的是( )
A.平分弦的查径垂直于弦
B.过三点可以确定一个圆
C.两圆的公共弦垂直平分连心线
D.等边三角形外接圆的面积是内切圆面积的4倍
【解答】解:A.平分弦(不是直径)的直径垂直于弦,故原说法错误;
B.不在同一直线上的三点确定一个圆,故原说法错误;
C.两圆的连心线垂直平分公共弦,故原说法错误;
D.如图,△ABC为等边三角形,⊙O为等边三角形的外接圆与内切圆,
∵△ABC为等边三角形,AD为角平分线,⊙O为△ABC的内切圆,连OB,如图,
∵△ABC为等边三角形,⊙O为△ABC的内切圆,
∴点O为△ABC的外心,AD⊥BC,
∴∠OBC=30°,
在Rt△OBD中,ODOB,
∴等边三角形外接圆的面积是内切圆面积的4倍,故原说法正确;
故选:D.
2.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
【解答】解⊙O的半径为3,
点M到圆心O的距离为1.5,
∴OM<r,
∴点M在圆内.
故选:C.
3.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
【解答】解:∵圆锥的高OA=8,底面半径OB=6,
∴在Rt△AOB中,母线AB,
故选:B.
4.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
【解答】解:∵四边形ABCD内接于⊙O,
∴∠C+∠A=180°,
∵∠C=110°,
∴∠A=180°﹣110°=70°,
由圆周角定理得:∠BOD=2∠A=140°,
故选:D.
5.(2025春 云岩区校级月考)如图,将△OAB绕着点O顺时针旋转60°后得到△OA′B′,若OB=5,则的长度为( )
A. B. C. D.
【解答】解:由旋转可知,∠BOB′=60°,
又因为OB=5,
所以的长度为.
故选:B.
6.(2025春 榆树市校级月考)如图,点A、B、C在⊙O上,且AB=AC.若∠ABO=21°,则∠BOC的大小为( )
A.42° B.82° C.84° D.90°
【解答】解:连接OA,
∵OA=OB=OC,
∴∠OAB=∠B,∠OAC=∠C,
∵AB=AC,
∴∠AOB=∠AOC,
∴∠BAO=∠OAC=∠B=21°,
∴∠BAC=∠BAO+∠CAO=42°,
∴∠BOC=2∠BAC=84°.
故选:C.
7.(2025春 袁州区校级月考)如图,AB为⊙O的直径,点C在⊙O上,连接BC.若AB=2,BC=1,则阴影部分的面积为( )
A. B. C.π D.
【解答】解:过O作OH⊥CD于H,
∵直径AB=2,BC=1,
∴OC=OB=BC=1,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠AOC=180°﹣60°=120°,
∴扇形OAC的面积,
∵△OBC是等边三角形,OH⊥BC,
∴CHBC,
∴OH,
∴△OBC的面积BC OH,
∴阴影部分的面积=扇形OAC的面积+△OBC的面积.
故选:D.
8.(2025春 大渡口区校级月考)如图,△ABC内接于⊙O,AB为⊙O的直径,直线CD与⊙O相切于点C,过点O作OE∥BC,交CD于点E,若∠BAC=32°,则∠OEC的度数为( )
A.34° B.32° C.26° D.58°
【解答】解:如图所示,连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠BAC=32°
∴∠ABC=58°,
又∵OC=OB,
∴∠OCB=∠ABC=58°,
∵OE∥BC,
∴∠EOC=58°,
∵直线CD与⊙O相切于点C,
∴∠ECO=90°,
∴∠OEC=90°﹣∠EOC=32°,
故选:B.
9.(2025 运城模拟)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD,BC.若∠BAC=32°,则∠D的度数为( )
A.68° B.58° C.32° D.64°
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=32°,
∴∠B=90°﹣∠BAC=90°﹣32°=58°,
∴∠D=∠B=58°.
故选:B.
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
【解答】解:由条件可知这条弦所对的圆心角的度数为,
∴这条弦与两条半径构成一个等腰直角三角形,
∴这条弦的长度为.
故答案为:.
11.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= 35° .
【解答】解:∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=20°,
∴∠AOB=90°﹣20°=70°,
∵OB=OC,
∴∠OBC(180°﹣70°)=55°,
∴∠ABC=90°﹣55°=35°,
故答案为:35°.
12.(2025 天河区校级二模)如图,已知一块圆心角为216°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),此圆锥形的烟囱帽底面圆的直径是60cm,则它的高是 40cm .
【解答】解:由题知,
圆锥的底面圆的周长为60π cm.
令圆锥的母线长为a cm,
则,
解得a=50,
所以圆锥的高为(cm).
故答案为:40cm.
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 7 .
【解答】解:如图,作圆O的直径DG,连接AG,
∴∠DAG=90°,
∴∠DAE+∠EAG=90°,
∵BC是⊙O的切线,
∴∠GDB=90°,
∴∠EDB+∠EDG=90°,
∵∠EAG=∠EDG,
∴∠EDB=∠DAE,
同理∠FDC=∠DAF,
连接DE,DF,
∵AD是△ABC的角平分线,
∴∠DAB=∠DAC,
∴∠CDF=∠EDB=∠DAC=∠EAD,
∴∠ADB=∠ADE+∠BDE=∠AFD,
∴△ADB∽△AFD,
∴,
∴6AB=(6)2,
∴AB=12,
∴BE=AB﹣AE=12﹣8=4,
∵∠B=∠B,∠BDE=∠EAD,
∴△EDB∽△DAB,
∴,
∴BD2=BE AB=4×12=48,
∴BD=4,
∵△ADB∽△AFD,
∴,
∴12DF=46,
∴DF=2,
∵∠CFD=∠AED,∠CDF=∠EAD,
∴△CDF∽△DAE,
∴,
∴,
∴CD=3,
∴BC=BD+CD=437.
故答案为:7.
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
【解答】解:如图,连接AC,
则∠DAC=∠DBC=25°,
∵,
∴∠ADB=∠DAC=25°,
∴∠AOB=2∠ADB=50°,
∵OA=3,
∴扇形AOB的面积为,
故答案为:
15.(2025春 乐陵市校级月考)如图,AE是△ABC的外接圆直径,点O为圆心.若∠BAE=25°,则∠C= 65° .
【解答】解:连接BE,
∵AE是△ABC的外接圆直径,
∴∠ABE=90°,
∴∠AEB=90°﹣∠BAE=90°﹣25°=65°.
∵,
∴∠C=∠AEB=65°.
故答案为:65°.
16.(2025春 中山市校级月考)如图所示的是一个半圆形拱桥的截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,已知拱桥的跨度AB=13m,若测得某时水面宽度CD=12m,则水深OE为 2.5m .
【解答】解:如图所示,连接OC,
∵OE⊥CD,
∴ECCD12=6(m),
∵OCAB13=6.5(m),
∴OE2.5(m),
∴水深OE为2.5m.
故答案为:2.5m.
17.(2025春 莘县校级月考)如图,扇形AOB的圆心角为60°,OA=5,点C在弧AB上,以OA,CA为邻边构造平行四边形ACDO,边CD交OB于点E,OB平分∠AOD,若OE=4,则图中阴影部分的面积为 .(结果保留π)
【解答】解:由条件可知OA∥CD,OA=CD=5,
∵扇形AOB的圆心角为60°,OB平分∠AOD,
∴∠OED=∠AOB=∠BOD=60°,
∴△DOE为等边三角形,
∴DE=OE=4,
∴CE=5﹣4=1,
如图,过E作EH⊥OA于H,
∴∠OEH=30°,
∴,,
∴,
故答案为:.
三.解答题(共6小题)
18.(2025春 集美区校级月考)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:AB=CD.
【解答】证明:∵AD=BC,
∴,
∵AC是⊙O的直径,
∴,
∴,
∴AB=CD.
19.(2025春 邳州市月考)如图,⊙O的直径AB⊥CD于点M,且M是半径OB的中点,CD=8cm.
(1)求直径AB的长;
(2)求弓形(阴影部分)的面积.
【解答】解:(1)连接OD,
∵AB⊥DC,CD=8cm,
∴DMcm.
∵M是半径OB的中点,
令⊙O的半径为r cm,
∴OM的长为 cm.
在Rt△ODM中,
,
解得r,
∴直径AB的长为cm.
(2)连接OC,
在Rt△ODM中,
∵OM,
∴∠ODM=30°.
又∵OD=OC,
∴∠ODM=∠OCM=30°,
∴∠COD=120°,
∴(cm2).
又∵(cm2),
∴(cm2).
20.(2024秋 合阳县期末)如图,AB为⊙O的直径,CB是⊙O的切线,切点为点B,点D为⊙O上一点,连接CD并延长交BA的延长线于点E,CD=CB.
(1)求证:CD是⊙O的切线;
(2)若AE=2,DE=4,求⊙O的半径长.
【解答】(1)证明:连接OD,
∵AB为⊙O的直径,CB与⊙O相切于点B,
∴CB⊥AB,
∴∠B=90°,
∵CD=CB,OD=OB,
∴CD2+OD2=CB2+OB2=OC2,
∴△ODC是直角三角形,且∠ODC=90°,
∵OD是⊙O的半径,且CD⊥OD,
∴CD是⊙O的切线.
(2)解:∵∠ODE=∠B=90°,
∴DE2+OD2=OE2,
∵AE=2,DE=4,OD=OA,
∴42+OA2=(2+OA)2,
解得OA=3,
∴⊙O的半径长为3.
21.(2025 驻马店二模)如图,AB为⊙O的直径,弦CD⊥AB,过点A作⊙O的切线交BC的延长线于点E.
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AD=6,求CE的长.
【解答】解:∵AE是⊙的切线,切点为A,
∴AE⊥AB,
∵CD⊥AB,
∴AE∥CD,
∴∠E=∠BCD,
∵∠BCD=∠BAD,
∴∠BAD=∠E;
(2)如图,连接AC,
∵AB为⊙O的直径,弦CD⊥AB,
∴,
∴AC=AD=6,
∵AB=2×5=10,
∴BC8,
∵tanB,
∴AE,
∴BE,
∴EC=EB﹣BC
8
,
即CE的长为.
22.(2025春 莘县校级月考)如图,△ABC内接于⊙O,BC是⊙O的直径,过点A作⊙O的切线交BC的延长线于点D,AE⊥BC于点F,交⊙O于点E.
(1)求证:∠DAE=2∠B;
(2)若CF=2OF,CD=12,求⊙O的半径.
【解答】(1)证明:△ABC内接于⊙O,BC是⊙O的直径,如图,连接OA,CE,
∴OA=OB,
∴∠B=∠BAO,
∵BC是⊙O的直径,⊙O的切线交BC的延长线于点D,AE⊥BC于点F,
∴∠BAC=∠DAO=90°,即∠BAO+∠OAC=∠OAC+∠DAC=90°,
∴∠BAO=∠DAC,
∴∠B=∠DAC,
∵AE⊥BC,
∴AC=CE,
∴∠CAE=∠AEC,
∵∠B=∠AEC,
∴∠B=∠CAE,
∴∠DAE=∠DAC+∠CAE=2∠B;
(2)解:∵∠DAC=∠B,∠D=∠D,
∴△DBA∽△DAC,
∴,
∴AD2=CD BD,
设OF=x,
∵CF=2OF,CD=12,
∴CF=2x,
∴OB=OC=OF+CF=3x,
∴BD=OB+OC+CD=6x+12,
∴AD2=12(6x+12)=144+72x,
在Rt△OAF中,OA=OB=3x,
由勾股定理得:AF2=OA2﹣OF2=8x2,
在Rt△AFD中,DF=CF+CD=12+2x,
由勾股定理得:AF2+DF2=AD2,
∴8x2+(12+2x)2=144+72x,即x2﹣2x=0,
解得:x=2或x=0(不合题意,舍去),
∴OC=3×2=6,
∴⊙O的半径为6.
23.(2025 新华区校级一模)如图1和图2,O为内、外两个圆的圆心,大圆被八等分,分点为A,B,C,D,E,F,G,H.已知两个圆的半径分别为1,3.
(1)如图1,若大圆中的弦AP与小圆相切于点M,求AP的长;
(2)通过计算比较弧AD的长和小圆的周长的大小;
(3)如图2,连接OB,AG,通过说理判断OB和AG的位置关系,并求点B到AG的距离.
【解答】解:(1)如图1,连接OA,OM,
∵大圆中的弦AP与小圆相切于点M,
∴OM⊥AP,
∴AM=PM,
在Rt△AOM中,OA=3,OM=1,
∴AM2,
∴;
(2)如图1,连接OD,
由题意得,
∴弧AD的长为.
小圆的周长为2π×1=2π,
∵,
∴弧AD的长大于小圆的周长;
(3)如图2,连接OA,OG,过点O作ON⊥AG于点N,
由题意得:,,OA=OG,
∴∠OAG=∠OGA=45°,
∴∠OAG=∠AOB,
∴OB∥AG,
在Rt△OAN中,,
∵OB∥AG,
∴点B到AG的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第24章圆同步练习卷-数学九年级上册人教版
一.选择题(共9小题)
1.(2025春 浦东新区校级月考)下列命题正确的是( )
A.平分弦的查径垂直于弦
B.过三点可以确定一个圆
C.两圆的公共弦垂直平分连心线
D.等边三角形外接圆的面积是内切圆面积的4倍
2.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
3.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
4.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
5.(2025春 云岩区校级月考)如图,将△OAB绕着点O顺时针旋转60°后得到△OA′B′,若OB=5,则的长度为( )
A. B. C. D.
6.(2025春 榆树市校级月考)如图,点A、B、C在⊙O上,且AB=AC.若∠ABO=21°,则∠BOC的大小为( )
A.42° B.82° C.84° D.90°
7.(2025春 袁州区校级月考)如图,AB为⊙O的直径,点C在⊙O上,连接BC.若AB=2,BC=1,则阴影部分的面积为( )
A. B. C.π D.
8.(2025春 大渡口区校级月考)如图,△ABC内接于⊙O,AB为⊙O的直径,直线CD与⊙O相切于点C,过点O作OE∥BC,交CD于点E,若∠BAC=32°,则∠OEC的度数为( )
A.34° B.32° C.26° D.58°
9.(2025 运城模拟)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD,BC.若∠BAC=32°,则∠D的度数为( )
A.68° B.58° C.32° D.64°
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
11.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= .
12.(2025 天河区校级二模)如图,已知一块圆心角为216°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),此圆锥形的烟囱帽底面圆的直径是60cm,则它的高是 .
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 .
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
15.(2025春 乐陵市校级月考)如图,AE是△ABC的外接圆直径,点O为圆心.若∠BAE=25°,则∠C= .
16.(2025春 中山市校级月考)如图所示的是一个半圆形拱桥的截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,已知拱桥的跨度AB=13m,若测得某时水面宽度CD=12m,则水深OE为 .
17.(2025春 莘县校级月考)如图,扇形AOB的圆心角为60°,OA=5,点C在弧AB上,以OA,CA为邻边构造平行四边形ACDO,边CD交OB于点E,OB平分∠AOD,若OE=4,则图中阴影部分的面积为 .(结果保留π)
三.解答题(共6小题)
18.(2025春 集美区校级月考)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:AB=CD.
19.(2025春 邳州市月考)如图,⊙O的直径AB⊥CD于点M,且M是半径OB的中点,CD=8cm.
(1)求直径AB的长;
(2)求弓形(阴影部分)的面积.
20.(2024秋 合阳县期末)如图,AB为⊙O的直径,CB是⊙O的切线,切点为点B,点D为⊙O上一点,连接CD并延长交BA的延长线于点E,CD=CB.
(1)求证:CD是⊙O的切线;
(2)若AE=2,DE=4,求⊙O的半径长.
21.(2025 驻马店二模)如图,AB为⊙O的直径,弦CD⊥AB,过点A作⊙O的切线交BC的延长线于点E.
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AD=6,求CE的长.
22.(2025春 莘县校级月考)如图,△ABC内接于⊙O,BC是⊙O的直径,过点A作⊙O的切线交BC的延长线于点D,AE⊥BC于点F,交⊙O于点E.
(1)求证:∠DAE=2∠B;
(2)若CF=2OF,CD=12,求⊙O的半径.
23.(2025 新华区校级一模)如图1和图2,O为内、外两个圆的圆心,大圆被八等分,分点为A,B,C,D,E,F,G,H.已知两个圆的半径分别为1,3.
(1)如图1,若大圆中的弦AP与小圆相切于点M,求AP的长;
(2)通过计算比较弧AD的长和小圆的周长的大小;
(3)如图2,连接OB,AG,通过说理判断OB和AG的位置关系,并求点B到AG的距离.
第24章圆同步练习卷-数学九年级上册人教版
参考答案与试题解析
一.选择题(共9小题)
题号 1 2 3 4 5 6 7 8 9
答案 D C B D B C D B B
一.选择题(共9小题)
1.(2025春 浦东新区校级月考)下列命题正确的是( )
A.平分弦的查径垂直于弦
B.过三点可以确定一个圆
C.两圆的公共弦垂直平分连心线
D.等边三角形外接圆的面积是内切圆面积的4倍
【解答】解:A.平分弦(不是直径)的直径垂直于弦,故原说法错误;
B.不在同一直线上的三点确定一个圆,故原说法错误;
C.两圆的连心线垂直平分公共弦,故原说法错误;
D.如图,△ABC为等边三角形,⊙O为等边三角形的外接圆与内切圆,
∵△ABC为等边三角形,AD为角平分线,⊙O为△ABC的内切圆,连OB,如图,
∵△ABC为等边三角形,⊙O为△ABC的内切圆,
∴点O为△ABC的外心,AD⊥BC,
∴∠OBC=30°,
在Rt△OBD中,ODOB,
∴等边三角形外接圆的面积是内切圆面积的4倍,故原说法正确;
故选:D.
2.(2024秋 杭州期末)已知⊙O的半径为3,点M到圆心O的距离为1.5,则点M在( )
A.圆外 B.圆上 C.圆内 D.不能确定
【解答】解⊙O的半径为3,
点M到圆心O的距离为1.5,
∴OM<r,
∴点M在圆内.
故选:C.
3.(2025春 东莞市期末)如图,一个圆锥的高OA=1,底面半径OB=1,则AB长为( )
A.1 B. C.2 D.3
【解答】解:∵圆锥的高OA=8,底面半径OB=6,
∴在Rt△AOB中,母线AB,
故选:B.
4.(2025春 青岛校级月考)如图,四边形ABCD内接于⊙O,连接OB,OD,BD,若∠C=110°,则∠BOD=( )
A.130° B.120° C.125° D.140°
【解答】解:∵四边形ABCD内接于⊙O,
∴∠C+∠A=180°,
∵∠C=110°,
∴∠A=180°﹣110°=70°,
由圆周角定理得:∠BOD=2∠A=140°,
故选:D.
5.(2025春 云岩区校级月考)如图,将△OAB绕着点O顺时针旋转60°后得到△OA′B′,若OB=5,则的长度为( )
A. B. C. D.
【解答】解:由旋转可知,∠BOB′=60°,
又因为OB=5,
所以的长度为.
故选:B.
6.(2025春 榆树市校级月考)如图,点A、B、C在⊙O上,且AB=AC.若∠ABO=21°,则∠BOC的大小为( )
A.42° B.82° C.84° D.90°
【解答】解:连接OA,
∵OA=OB=OC,
∴∠OAB=∠B,∠OAC=∠C,
∵AB=AC,
∴∠AOB=∠AOC,
∴∠BAO=∠OAC=∠B=21°,
∴∠BAC=∠BAO+∠CAO=42°,
∴∠BOC=2∠BAC=84°.
故选:C.
7.(2025春 袁州区校级月考)如图,AB为⊙O的直径,点C在⊙O上,连接BC.若AB=2,BC=1,则阴影部分的面积为( )
A. B. C.π D.
【解答】解:过O作OH⊥CD于H,
∵直径AB=2,BC=1,
∴OC=OB=BC=1,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠AOC=180°﹣60°=120°,
∴扇形OAC的面积,
∵△OBC是等边三角形,OH⊥BC,
∴CHBC,
∴OH,
∴△OBC的面积BC OH,
∴阴影部分的面积=扇形OAC的面积+△OBC的面积.
故选:D.
8.(2025春 大渡口区校级月考)如图,△ABC内接于⊙O,AB为⊙O的直径,直线CD与⊙O相切于点C,过点O作OE∥BC,交CD于点E,若∠BAC=32°,则∠OEC的度数为( )
A.34° B.32° C.26° D.58°
【解答】解:如图所示,连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠BAC=32°
∴∠ABC=58°,
又∵OC=OB,
∴∠OCB=∠ABC=58°,
∵OE∥BC,
∴∠EOC=58°,
∵直线CD与⊙O相切于点C,
∴∠ECO=90°,
∴∠OEC=90°﹣∠EOC=32°,
故选:B.
9.(2025 运城模拟)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD,BC.若∠BAC=32°,则∠D的度数为( )
A.68° B.58° C.32° D.64°
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=32°,
∴∠B=90°﹣∠BAC=90°﹣32°=58°,
∴∠D=∠B=58°.
故选:B.
二.填空题(共8小题)
10.(2025春 浦东新区校级月考)若⊙O的半径为3cm,一条弦分⊙O为1:3两部分,这条弦的长度为 .
【解答】解:由条件可知这条弦所对的圆心角的度数为,
∴这条弦与两条半径构成一个等腰直角三角形,
∴这条弦的长度为.
故答案为:.
11.(2025 椒江区校级模拟)如图,AB与⊙O相切于点B,连结OA交⊙O于点C,连结OB,BC,若∠A=20°,则∠ABC= 35° .
【解答】解:∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=20°,
∴∠AOB=90°﹣20°=70°,
∵OB=OC,
∴∠OBC(180°﹣70°)=55°,
∴∠ABC=90°﹣55°=35°,
故答案为:35°.
12.(2025 天河区校级二模)如图,已知一块圆心角为216°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),此圆锥形的烟囱帽底面圆的直径是60cm,则它的高是 40cm .
【解答】解:由题知,
圆锥的底面圆的周长为60π cm.
令圆锥的母线长为a cm,
则,
解得a=50,
所以圆锥的高为(cm).
故答案为:40cm.
13.(2024秋 海曙区期末)如图,AD是△ABC的角平分线,过点A、D的圆与BC相切,与边AB、AC分别交于点E、F.若,AE=8,AF=6,则BC的长为 7 .
【解答】解:如图,作圆O的直径DG,连接AG,
∴∠DAG=90°,
∴∠DAE+∠EAG=90°,
∵BC是⊙O的切线,
∴∠GDB=90°,
∴∠EDB+∠EDG=90°,
∵∠EAG=∠EDG,
∴∠EDB=∠DAE,
同理∠FDC=∠DAF,
连接DE,DF,
∵AD是△ABC的角平分线,
∴∠DAB=∠DAC,
∴∠CDF=∠EDB=∠DAC=∠EAD,
∴∠ADB=∠ADE+∠BDE=∠AFD,
∴△ADB∽△AFD,
∴,
∴6AB=(6)2,
∴AB=12,
∴BE=AB﹣AE=12﹣8=4,
∵∠B=∠B,∠BDE=∠EAD,
∴△EDB∽△DAB,
∴,
∴BD2=BE AB=4×12=48,
∴BD=4,
∵△ADB∽△AFD,
∴,
∴12DF=46,
∴DF=2,
∵∠CFD=∠AED,∠CDF=∠EAD,
∴△CDF∽△DAE,
∴,
∴,
∴CD=3,
∴BC=BD+CD=437.
故答案为:7.
14.(2025春 青岛校级月考)如图,A,B,C,D是⊙O上的点,半径OA=3,,∠DBC=25°,连接AD,则扇形AOB的面积为 .
【解答】解:如图,连接AC,
则∠DAC=∠DBC=25°,
∵,
∴∠ADB=∠DAC=25°,
∴∠AOB=2∠ADB=50°,
∵OA=3,
∴扇形AOB的面积为,
故答案为:
15.(2025春 乐陵市校级月考)如图,AE是△ABC的外接圆直径,点O为圆心.若∠BAE=25°,则∠C= 65° .
【解答】解:连接BE,
∵AE是△ABC的外接圆直径,
∴∠ABE=90°,
∴∠AEB=90°﹣∠BAE=90°﹣25°=65°.
∵,
∴∠C=∠AEB=65°.
故答案为:65°.
16.(2025春 中山市校级月考)如图所示的是一个半圆形拱桥的截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,已知拱桥的跨度AB=13m,若测得某时水面宽度CD=12m,则水深OE为 2.5m .
【解答】解:如图所示,连接OC,
∵OE⊥CD,
∴ECCD12=6(m),
∵OCAB13=6.5(m),
∴OE2.5(m),
∴水深OE为2.5m.
故答案为:2.5m.
17.(2025春 莘县校级月考)如图,扇形AOB的圆心角为60°,OA=5,点C在弧AB上,以OA,CA为邻边构造平行四边形ACDO,边CD交OB于点E,OB平分∠AOD,若OE=4,则图中阴影部分的面积为 .(结果保留π)
【解答】解:由条件可知OA∥CD,OA=CD=5,
∵扇形AOB的圆心角为60°,OB平分∠AOD,
∴∠OED=∠AOB=∠BOD=60°,
∴△DOE为等边三角形,
∴DE=OE=4,
∴CE=5﹣4=1,
如图,过E作EH⊥OA于H,
∴∠OEH=30°,
∴,,
∴,
故答案为:.
三.解答题(共6小题)
18.(2025春 集美区校级月考)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:AB=CD.
【解答】证明:∵AD=BC,
∴,
∵AC是⊙O的直径,
∴,
∴,
∴AB=CD.
19.(2025春 邳州市月考)如图,⊙O的直径AB⊥CD于点M,且M是半径OB的中点,CD=8cm.
(1)求直径AB的长;
(2)求弓形(阴影部分)的面积.
【解答】解:(1)连接OD,
∵AB⊥DC,CD=8cm,
∴DMcm.
∵M是半径OB的中点,
令⊙O的半径为r cm,
∴OM的长为 cm.
在Rt△ODM中,
,
解得r,
∴直径AB的长为cm.
(2)连接OC,
在Rt△ODM中,
∵OM,
∴∠ODM=30°.
又∵OD=OC,
∴∠ODM=∠OCM=30°,
∴∠COD=120°,
∴(cm2).
又∵(cm2),
∴(cm2).
20.(2024秋 合阳县期末)如图,AB为⊙O的直径,CB是⊙O的切线,切点为点B,点D为⊙O上一点,连接CD并延长交BA的延长线于点E,CD=CB.
(1)求证:CD是⊙O的切线;
(2)若AE=2,DE=4,求⊙O的半径长.
【解答】(1)证明:连接OD,
∵AB为⊙O的直径,CB与⊙O相切于点B,
∴CB⊥AB,
∴∠B=90°,
∵CD=CB,OD=OB,
∴CD2+OD2=CB2+OB2=OC2,
∴△ODC是直角三角形,且∠ODC=90°,
∵OD是⊙O的半径,且CD⊥OD,
∴CD是⊙O的切线.
(2)解:∵∠ODE=∠B=90°,
∴DE2+OD2=OE2,
∵AE=2,DE=4,OD=OA,
∴42+OA2=(2+OA)2,
解得OA=3,
∴⊙O的半径长为3.
21.(2025 驻马店二模)如图,AB为⊙O的直径,弦CD⊥AB,过点A作⊙O的切线交BC的延长线于点E.
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AD=6,求CE的长.
【解答】解:∵AE是⊙的切线,切点为A,
∴AE⊥AB,
∵CD⊥AB,
∴AE∥CD,
∴∠E=∠BCD,
∵∠BCD=∠BAD,
∴∠BAD=∠E;
(2)如图,连接AC,
∵AB为⊙O的直径,弦CD⊥AB,
∴,
∴AC=AD=6,
∵AB=2×5=10,
∴BC8,
∵tanB,
∴AE,
∴BE,
∴EC=EB﹣BC
8
,
即CE的长为.
22.(2025春 莘县校级月考)如图,△ABC内接于⊙O,BC是⊙O的直径,过点A作⊙O的切线交BC的延长线于点D,AE⊥BC于点F,交⊙O于点E.
(1)求证:∠DAE=2∠B;
(2)若CF=2OF,CD=12,求⊙O的半径.
【解答】(1)证明:△ABC内接于⊙O,BC是⊙O的直径,如图,连接OA,CE,
∴OA=OB,
∴∠B=∠BAO,
∵BC是⊙O的直径,⊙O的切线交BC的延长线于点D,AE⊥BC于点F,
∴∠BAC=∠DAO=90°,即∠BAO+∠OAC=∠OAC+∠DAC=90°,
∴∠BAO=∠DAC,
∴∠B=∠DAC,
∵AE⊥BC,
∴AC=CE,
∴∠CAE=∠AEC,
∵∠B=∠AEC,
∴∠B=∠CAE,
∴∠DAE=∠DAC+∠CAE=2∠B;
(2)解:∵∠DAC=∠B,∠D=∠D,
∴△DBA∽△DAC,
∴,
∴AD2=CD BD,
设OF=x,
∵CF=2OF,CD=12,
∴CF=2x,
∴OB=OC=OF+CF=3x,
∴BD=OB+OC+CD=6x+12,
∴AD2=12(6x+12)=144+72x,
在Rt△OAF中,OA=OB=3x,
由勾股定理得:AF2=OA2﹣OF2=8x2,
在Rt△AFD中,DF=CF+CD=12+2x,
由勾股定理得:AF2+DF2=AD2,
∴8x2+(12+2x)2=144+72x,即x2﹣2x=0,
解得:x=2或x=0(不合题意,舍去),
∴OC=3×2=6,
∴⊙O的半径为6.
23.(2025 新华区校级一模)如图1和图2,O为内、外两个圆的圆心,大圆被八等分,分点为A,B,C,D,E,F,G,H.已知两个圆的半径分别为1,3.
(1)如图1,若大圆中的弦AP与小圆相切于点M,求AP的长;
(2)通过计算比较弧AD的长和小圆的周长的大小;
(3)如图2,连接OB,AG,通过说理判断OB和AG的位置关系,并求点B到AG的距离.
【解答】解:(1)如图1,连接OA,OM,
∵大圆中的弦AP与小圆相切于点M,
∴OM⊥AP,
∴AM=PM,
在Rt△AOM中,OA=3,OM=1,
∴AM2,
∴;
(2)如图1,连接OD,
由题意得,
∴弧AD的长为.
小圆的周长为2π×1=2π,
∵,
∴弧AD的长大于小圆的周长;
(3)如图2,连接OA,OG,过点O作ON⊥AG于点N,
由题意得:,,OA=OG,
∴∠OAG=∠OGA=45°,
∴∠OAG=∠AOB,
∴OB∥AG,
在Rt△OAN中,,
∵OB∥AG,
∴点B到AG的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
