第三章圆锥曲线的方程检测卷(含解析)-2025-2026学年高二数学上学期人教A版2019选择性必修第一册
文档属性
| 名称 | 第三章圆锥曲线的方程检测卷(含解析)-2025-2026学年高二数学上学期人教A版2019选择性必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 497.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章圆锥曲线的方程检测卷-2025-2026学年高二数学上学期人教A版2019选择性必修第一册
一.选择题(共8小题)
1.(2025春 新化县校级月考)抛物线y=﹣5x2的准线方程为( )
A. B. C. D.
2.(2026春 江汉区月考)已知双曲线,则C的右焦点到其渐近线的距离为( )
A.2 B.6 C. D.
3.(2024秋 朝阳校级期末)已知抛物线C:y2=2x,过点的直线l与C相交于A,B两点,且M为弦AB的中点,则直线l的方程为( )
A.6x+6y﹣7=0 B.6x﹣6y﹣1=0
C.2x﹣6y﹣5=0 D.12x﹣6y﹣5=0
4.(2024秋 安徽期末)已知椭圆的左、右焦点分别为F1,F2,且椭圆上存在点P,使得|PF1|=7|PF2|,则该椭圆的离心率的取值范围是( )
A. B. C. D.
5.(2025 保山校级一模)双曲线的左、右焦点分别为F1、F2.过F2作其中一条渐近线的垂线,垂足为P.已知PF2=2,直线PF1的斜率为,则双曲线的方程为( )
A. B.1
C. D.
6.(2025 临翔区校级模拟)已知双曲线E的右焦点为F,以F为圆心,为半径的圆与双曲线E的一条渐近线交于A,B两点,若,则双曲线E的离心率为( )
A. B. C. D.3
7.(2025春 张掖月考)已知平行四边形ABCD内接于椭圆Ω:,且AB,AD斜率之积的范围为,则椭圆Ω离心率的取值范围是( )
A. B.
C. D.
8.(2024秋 清远期末)已知双曲线C:的离心率为,右焦点F到其渐近线的距离为,过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,则( )
A.2 B. C.1 D.
二.多选题(共3小题)
(多选)9.(2025春 揭阳月考)以两条直线5x±3y﹣2=0为渐近线的双曲线的离心率可以是( )
A. B. C. D.
(多选)10.(2024秋 厦门校级期末)已知双曲线C:,则下列说法正确的是( )
A.双曲线C的实轴长为2
B.双曲线C的焦点到渐近线的距离为m
C.若(2,0)是双曲线C的一个焦点,则m=2
D.若双曲线C的两条渐近线相互垂直,则m=2
(多选)11.(2025春 望城区校级期末)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点,若∠ABD=90°,且△ABF的面积为,则( )
A.|BF|=4
B.△ABF是等边三角形
C.△BDF的面积为
D.抛物线C的方程为y2=4x
三.填空题(共3小题)
12.(2025春 甘肃月考)已知椭圆的左、右焦点分别为F1,F2,过F1作斜率为的直线l交E于第一象限的点A,则△AF1F2外接圆的半径为 .
13.(2025春 崂山区校级期中)已知直线l过双曲线的右焦点,且与双曲线交于A,B两点,则|AB|的最小值为 .
14.(2025春 集宁区校级期中)已知抛物线的方程为y2=4x,过其焦点F的直线交此抛物线于M、N两点,交y轴于点E,若,,则λ1+λ2= .
四.解答题(共5小题)
15.(2025春 科左中旗校级期末)已知焦点位于x轴的抛物线C过点M(1,2).
(1)求抛物线C的方程,并求其准线方程;
(2)过该抛物线的焦点,作倾斜角为60°的直线,交抛物线于A,B两点,求线段AB的长度.
16.(2024秋 南开区校级期末)设椭圆,且离心率为,过点P(4,0)的直线与椭圆交于A,B两点,当直线AB经过椭圆中心O时,|AB|=4.
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知点T(1,1),直线AT和直线BT分别与y轴交于C,D,与x轴交于E,F,若3S△CDT=S△EFT,求直线AB的斜率.
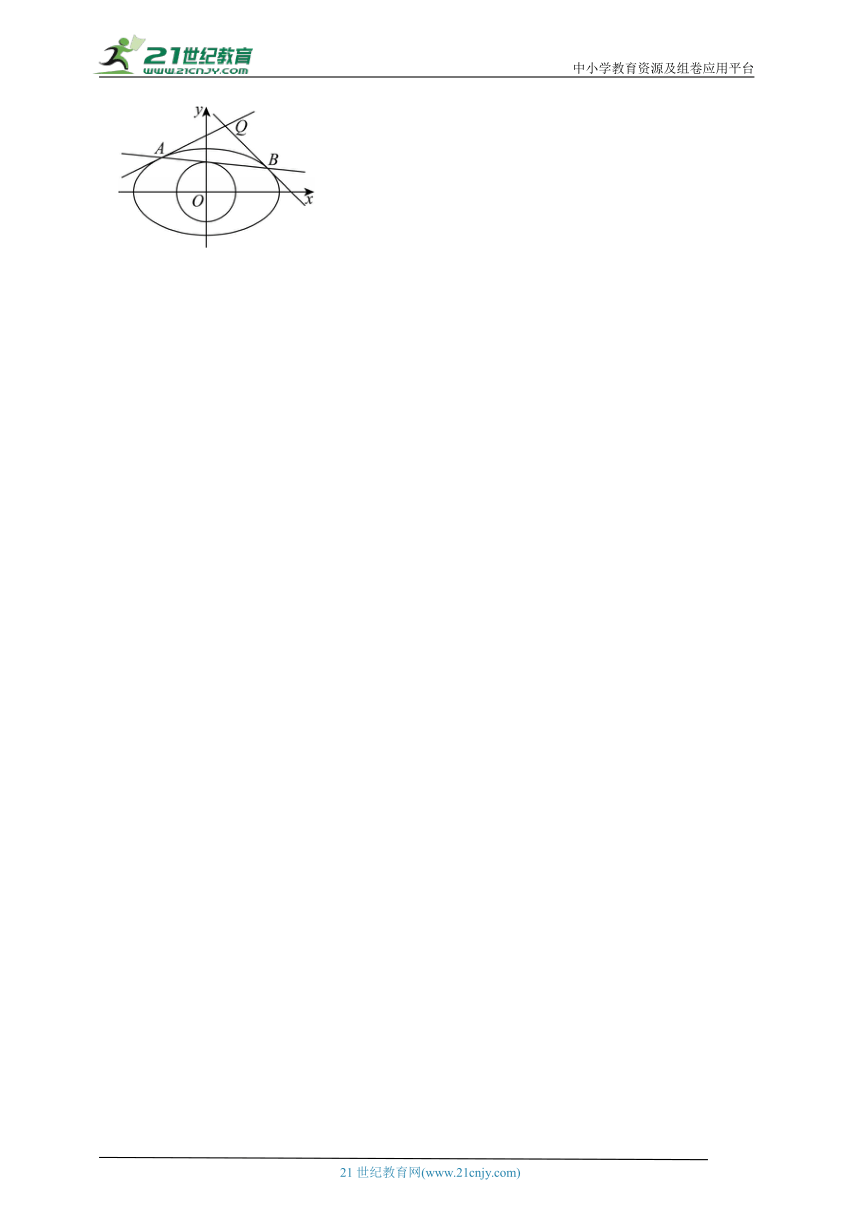
17.(2024秋 杨浦区校级期末)已知过点的双曲线C的渐近线方程为.如图所示,过双曲线C的右焦点F作与坐标轴都不垂直的直线l交C的右支于A,B两点.
(1)求双曲线C的标准方程;
(2)若双曲线C上的点Q(x0,y0)到其两条渐近线的距离分别为d1,d2,求d1d2的值;
(3)已知点,求证:∠AQF=∠BQF.
18.(2025春 丽水月考)已知椭圆Γ的方程为,椭圆Γ的左、右焦点分别为F1、F2,过F2的直线l与椭圆Γ交于P、Q两点(P、Q均不在x轴上).
(1)若椭圆Γ的离心率为,求a的值;
(2)若a=2,左顶点为A,求△APQ的面积的最大值.
19.(2025春 峨山县校级期末)已知直线l:y=kx+b与圆O:x2+y2=1相切.
(1)求k2﹣b2的值;
(2)已知椭圆E:在点P(x0,y0)处的切线方程为,若直线l与椭圆E相交于A,B两点,分别过A,B作椭圆E的切线,两条切线相交于点Q,求点Q的轨迹方程;
(3)是否存在这样的二次曲线F:λx2+μy2=1,当直线l与曲线F有两个交点M,N时,总有OM⊥ON?若存在,求出λ+μ的值;若不存在,请说明理由.
第三章圆锥曲线的方程检测卷-2025-2026学年高二数学上学期人教A版2019选择性必修第一册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A B D C D A A D
二.多选题(共3小题)
题号 9 10 11
答案 BD CD ABD
一.选择题(共8小题)
1.(2025春 新化县校级月考)抛物线y=﹣5x2的准线方程为( )
A. B. C. D.
【解答】解:由题可得抛物线方程为:,
2p,且开口向下,
所以抛物线y=﹣5x2的准线方程为.
故选:A.
2.(2026春 江汉区月考)已知双曲线,则C的右焦点到其渐近线的距离为( )
A.2 B.6 C. D.
【解答】解:双曲线,
a2=4,b2=36,∴,
∴右焦点坐标为,其中一条渐近线方程为y=3x,
∴右焦点到其渐近线的距离为.
故选:B.
3.(2024秋 朝阳校级期末)已知抛物线C:y2=2x,过点的直线l与C相交于A,B两点,且M为弦AB的中点,则直线l的方程为( )
A.6x+6y﹣7=0 B.6x﹣6y﹣1=0
C.2x﹣6y﹣5=0 D.12x﹣6y﹣5=0
【解答】解:已知抛物线C:y2=2x,过点的直线l与C相交于A,B两点,且M为弦AB的中点,
显然直线l不垂直于y,设直线l的方程为,
由,
消去x得,
由弦AB的中点为,
得,
此时方程有两个不等实根,
所以直线l的方程为,
即直线l的方程为12x﹣6y﹣5=0.
故选:D.
4.(2024秋 安徽期末)已知椭圆的左、右焦点分别为F1,F2,且椭圆上存在点P,使得|PF1|=7|PF2|,则该椭圆的离心率的取值范围是( )
A. B. C. D.
【解答】解:由椭圆的定义得|PF1|+|PF2|=2a,又|PF1|=7|PF2|,所以,
又a﹣c≤|PF1|≤a+c,a﹣c≤|PF2|≤a+c,
所以a≤a+c,且a﹣ca,所以,即,
即椭圆的离心率的取值范围是.
故选:C.
5.(2025 保山校级一模)双曲线的左、右焦点分别为F1、F2.过F2作其中一条渐近线的垂线,垂足为P.已知PF2=2,直线PF1的斜率为,则双曲线的方程为( )
A. B.1
C. D.
【解答】解:根据对称性,不妨设双曲线的其中一条渐近线方程为,
则过F2(c,0)且垂直渐近线的直线方程为,
联立,可得P(,),
∴|PF2|b=2,又F1(﹣c,0),
∴,∴,
∴,∴a,又b=2,
∴双曲线的方程为.
故选:D.
6.(2025 临翔区校级模拟)已知双曲线E的右焦点为F,以F为圆心,为半径的圆与双曲线E的一条渐近线交于A,B两点,若,则双曲线E的离心率为( )
A. B. C. D.3
【解答】解:令点F(c,0),双曲线E 的渐近线方程为,
由对称性不妨取直线AB:bx﹣ay=0,取AB中点C,连接FC,则FC⊥AB,
,而,
由,得|OC|=|AB|=2b,在Rt△OCF中,c2=(2b)2+b2=5b2,
则a2=c2﹣b2=4b2,解得,
所以双曲线 E的离心率.
故选:A.
7.(2025春 张掖月考)已知平行四边形ABCD内接于椭圆Ω:,且AB,AD斜率之积的范围为,则椭圆Ω离心率的取值范围是( )
A. B.
C. D.
【解答】解:已知平行四边形ABCD内接于椭圆Ω:,
且AB,AD斜率之积的范围为,
则A,C和B,D均关于原点对称,令B(m,n),则D(﹣m,﹣n),
若A(x,y),则,
所以椭圆Ω离心率.
故选:A.
8.(2024秋 清远期末)已知双曲线C:的离心率为,右焦点F到其渐近线的距离为,过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,则( )
A.2 B. C.1 D.
【解答】解:∵双曲线C:的离心率为,右焦点F到其渐近线的距离为,
∴由题知,解得,
∴双曲线C:,∴F(3,0),
依题意可设PQ:x=my+3,
代入双曲线C:,消去x,整理得(m2﹣2)y2+6my+3=0,
设P(x1,y1),Q(x2,y2),y1>y2,
则,又M(,),N(2,),
∴k1﹣k2,
∵S|OF| (y1﹣y2)(y1﹣y2),
∴.
故选:D.
二.多选题(共3小题)
(多选)9.(2025春 揭阳月考)以两条直线5x±3y﹣2=0为渐近线的双曲线的离心率可以是( )
A. B. C. D.
【解答】解:根据渐近线方程5x±3y﹣2=0可得,双曲线的渐近线斜率为.
根据双曲线渐近线方程的性质可得或.
①当时,,
∴,则
②当时,,
∴,则,
∴以两条直线5x±3y﹣2=0为渐近线的双曲线的离心率可以是或.
故选:BD.
(多选)10.(2024秋 厦门校级期末)已知双曲线C:,则下列说法正确的是( )
A.双曲线C的实轴长为2
B.双曲线C的焦点到渐近线的距离为m
C.若(2,0)是双曲线C的一个焦点,则m=2
D.若双曲线C的两条渐近线相互垂直,则m=2
【解答】解:∵曲线C:为双曲线,
∴m>0,且a,b,则双曲线C的实轴长为2,故A错误;
取双曲线一个焦点F(c,0),一条渐近线方程为y,即bx﹣ay=0,
则双曲线C的焦点到渐近线的距离为,故B错误;
若(2,0)是双曲线C的一个焦点,则2+m=4,得m=2,故C正确;
若双曲线C的两条渐近线相互垂直,则,即m=2,故D正确.
故选:CD.
(多选)11.(2025春 望城区校级期末)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点,若∠ABD=90°,且△ABF的面积为,则( )
A.|BF|=4
B.△ABF是等边三角形
C.△BDF的面积为
D.抛物线C的方程为y2=4x
【解答】解:抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点,
设准线l与x轴交于点M,如图,
抛物线定义知|AB|=|AF|,又|BF|=|AF|,所以△ABF为正三角形,故B正确;
由△ABF面积为知△ABF边长|BF|=4,故A正确;
则由直角三角形MBF可得p=2|OF|=|MF|=4cos60°=2,
所以抛物线C的方程为y2=4x,故D正确;
△BDF面积为,故C错误.
故选:ABD.
三.填空题(共3小题)
12.(2025春 甘肃月考)已知椭圆的左、右焦点分别为F1,F2,过F1作斜率为的直线l交E于第一象限的点A,则△AF1F2外接圆的半径为 .
【解答】解:已知椭圆的左、右焦点分别为F1,F2,过F1作斜率为的直线l交E于第一象限的点A,
因为∠AF1F2∈(0,π),且,
解得,,
又,
设|AF2|=t,则|AF1|=6﹣t,
由余弦定理知,
即,
解得t=2,
即|AF2|=2,|AF1|=4,
则易知AF2⊥l,
故,
即△AF1F2的外接圆半径为.
故答案为:.
13.(2025春 崂山区校级期中)已知直线l过双曲线的右焦点,且与双曲线交于A,B两点,则|AB|的最小值为 5 .
【解答】解:在双曲线C:中,a2=4,b2=5,则,所以右焦点坐标为(3,0),
当直线l垂直于x轴时,直线l与双曲线的交点A、B的横坐标都为3,
将x=3代入双曲线方程,可得,解得,
此时;
当直线l不垂直于x轴时,设直线l的方程为y=k(x﹣3),A(x1,y1),B(x2,y2),
将y=k(x﹣3)代入双曲线方程,整理可得(5﹣4k2)x2+24k2x﹣36k2﹣20=0,
Δ=(24k2)2﹣4×(5﹣4k2)×(﹣36k2﹣20)=400k2+400>0,
由韦达定理可知,,
则|AB|
|5|>5,
所以|AB|的最小值为5.
故答案为:5.
14.(2025春 集宁区校级期中)已知抛物线的方程为y2=4x,过其焦点F的直线交此抛物线于M、N两点,交y轴于点E,若,,则λ1+λ2= ﹣1 .
【解答】解:由抛物线的方程为y2=4x,
得F(1,0),
由题意可得直线MN的斜率存在且不等于零,
则可设直线MN的方程为x=my+1(m≠0),M(x1,y1),N(x2,y2),
联立,
消x得y2﹣4my﹣4=0,
则Δ=16m2+16>0恒成立,
则y1+y2=4m,y1y2=﹣4,
故,
由直线x=my+1(m≠0),
令x=0,
得,
则,
由,
得,
所以x1=λ1(1﹣x1),
所以,
由,
得,
所以x2=λ2(1﹣x2),
所以,
所以
.
故答案为:﹣1.
四.解答题(共5小题)
15.(2025春 科左中旗校级期末)已知焦点位于x轴的抛物线C过点M(1,2).
(1)求抛物线C的方程,并求其准线方程;
(2)过该抛物线的焦点,作倾斜角为60°的直线,交抛物线于A,B两点,求线段AB的长度.
【解答】解:(1)由题意可知,抛物线C的焦点位于x轴正半轴,
设抛物线C的方程为y2=2px(p>0),
因为抛物线C过点M(1,2),
所以2p=4,解得p=2,
故抛物线C的方程为y2=4x,其准线方程为x=﹣1.
(2)由(1)知,抛物线C的焦点为F(1,0),
因为直线AB的倾斜角为60°,且过抛物线C的焦点F,
所以直线AB的方程为,
由,得3x2﹣10x+3=0,
设A(x1,y1),B(x2,y2),则,
所以.
16.(2024秋 南开区校级期末)设椭圆,且离心率为,过点P(4,0)的直线与椭圆交于A,B两点,当直线AB经过椭圆中心O时,|AB|=4.
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知点T(1,1),直线AT和直线BT分别与y轴交于C,D,与x轴交于E,F,若3S△CDT=S△EFT,求直线AB的斜率.
【解答】解:(Ⅰ)当直线AB经过椭圆中心O时,可知|AB|=2a=4,所以a=2,
又因为离心率,因此,所以b2=a2﹣c2=1,
因此椭圆方程;
(Ⅱ)①当直线AB的方程为y=0时,易知B(2,0),A(﹣2,0);
直线BT的方程为y=﹣x+2,因此D(0,2);
直线AT的方程为,因此;
此时点点F与点B重合,E与点A重合,易知3S△CDT=S△EFT;
②设直线AB为x=my+4,B(x2,y2),A(x1,y1),
所以,
根的判别式Δ=64m2﹣48(m2+4)>0,解得m2﹣12>0,
所以或,且;
所以根据韦达定理可得,,
所以,,
所以3S△CDT=S△EFT 3CD=EF 3|yC﹣yD|=|xE﹣xF|
直线,直线,
令y=0,,,
令x=0,,,
所以
所以|x1x2﹣(x1+x2)+1|=3|y1y2﹣(y1+y2)+1|,
所以|﹣4m2+64﹣32+m2+4|=3|12+8m+m2+4|,
即|﹣3m2+36|=3|m2+8m+16|.
所以24m+84=0,解得,斜率为;
综上所述,直线AB的斜率为0或.
17.(2024秋 杨浦区校级期末)已知过点的双曲线C的渐近线方程为.如图所示,过双曲线C的右焦点F作与坐标轴都不垂直的直线l交C的右支于A,B两点.
(1)求双曲线C的标准方程;
(2)若双曲线C上的点Q(x0,y0)到其两条渐近线的距离分别为d1,d2,求d1d2的值;
(3)已知点,求证:∠AQF=∠BQF.
【解答】解:(1)因为双曲线C的渐近线方程为,
所以设双曲线方程为x2﹣3y2=λ(λ≠0),
又双曲线过点,
则λ=9﹣3×2=3,所以双曲线的方程为x2﹣3y2=3,
即.
(2)因为Q(x0,y0)在曲线上,
则,
渐近线方程:,
所以.
(3)证明:由(1)可知F(2,0),l的斜率存在且不为0,设l的方程为y=k(x﹣2),
联立,消去y得(1﹣3k2)x2+12k2x﹣12k2﹣3=0,
设A(x1,y1),B(x2,y2),由题意得,
则,
所以
,
所以kAQ=﹣kBQ,∠AQF=∠BQF得证.
18.(2025春 丽水月考)已知椭圆Γ的方程为,椭圆Γ的左、右焦点分别为F1、F2,过F2的直线l与椭圆Γ交于P、Q两点(P、Q均不在x轴上).
(1)若椭圆Γ的离心率为,求a的值;
(2)若a=2,左顶点为A,求△APQ的面积的最大值.
【解答】解:(1)因为椭圆Γ的离心率为,
因此,
解得.
(2)a=2时,c2=a2﹣1=3,故,因此,,
P、Q均不在x轴上,故直线l的斜率不为0,
设直线l的方程为,P(x1,y1),Q(x2,y2),
联立与得,
因Δ=12m2+4(m2+4)=16m2+16>0,
由韦达定理,,,
因此,
代入,,原式得,
又,故△APQ的面积,
而,
当且仅当,即m2=2时等号成立,
因此△APQ的面积的最大值为.
19.(2025春 峨山县校级期末)已知直线l:y=kx+b与圆O:x2+y2=1相切.
(1)求k2﹣b2的值;
(2)已知椭圆E:在点P(x0,y0)处的切线方程为,若直线l与椭圆E相交于A,B两点,分别过A,B作椭圆E的切线,两条切线相交于点Q,求点Q的轨迹方程;
(3)是否存在这样的二次曲线F:λx2+μy2=1,当直线l与曲线F有两个交点M,N时,总有OM⊥ON?若存在,求出λ+μ的值;若不存在,请说明理由.
【解答】解:(1)因为直线l与圆O相切,
所以圆心O到直线l的距离,
则k2﹣b2=﹣1;
(2)设A(x1,y1),B(x2,y2),Q(x0,y0),
可得椭圆E在点A(x1,y1)处的切线AQ方程为,
因为点Q(x0,y0)在切线AQ上,
所以,①
同理得,②
由①②得A(x1,y1),B(x2,y2)都在直线上,
所以直线AB方程为,③
因为圆O与直线AB相切,
所以点O到直线AB的距离,
所以,
因为点Q(x0,y0)具有任意性,
则点Q的轨迹方程为;
(3)假设存在曲线F满足条件,设M(x3,y3),N(x4,y4),
联立,消去y并整理得(λ+μk2)x2+2kbμy+μb2﹣1=0,
此时Δ>0,
由韦达定理得.
因为OM⊥ON,
所以
恒成立.
故所以存在曲线F,且λ+μ=1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章圆锥曲线的方程检测卷-2025-2026学年高二数学上学期人教A版2019选择性必修第一册
一.选择题(共8小题)
1.(2025春 新化县校级月考)抛物线y=﹣5x2的准线方程为( )
A. B. C. D.
2.(2026春 江汉区月考)已知双曲线,则C的右焦点到其渐近线的距离为( )
A.2 B.6 C. D.
3.(2024秋 朝阳校级期末)已知抛物线C:y2=2x,过点的直线l与C相交于A,B两点,且M为弦AB的中点,则直线l的方程为( )
A.6x+6y﹣7=0 B.6x﹣6y﹣1=0
C.2x﹣6y﹣5=0 D.12x﹣6y﹣5=0
4.(2024秋 安徽期末)已知椭圆的左、右焦点分别为F1,F2,且椭圆上存在点P,使得|PF1|=7|PF2|,则该椭圆的离心率的取值范围是( )
A. B. C. D.
5.(2025 保山校级一模)双曲线的左、右焦点分别为F1、F2.过F2作其中一条渐近线的垂线,垂足为P.已知PF2=2,直线PF1的斜率为,则双曲线的方程为( )
A. B.1
C. D.
6.(2025 临翔区校级模拟)已知双曲线E的右焦点为F,以F为圆心,为半径的圆与双曲线E的一条渐近线交于A,B两点,若,则双曲线E的离心率为( )
A. B. C. D.3
7.(2025春 张掖月考)已知平行四边形ABCD内接于椭圆Ω:,且AB,AD斜率之积的范围为,则椭圆Ω离心率的取值范围是( )
A. B.
C. D.
8.(2024秋 清远期末)已知双曲线C:的离心率为,右焦点F到其渐近线的距离为,过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,则( )
A.2 B. C.1 D.
二.多选题(共3小题)
(多选)9.(2025春 揭阳月考)以两条直线5x±3y﹣2=0为渐近线的双曲线的离心率可以是( )
A. B. C. D.
(多选)10.(2024秋 厦门校级期末)已知双曲线C:,则下列说法正确的是( )
A.双曲线C的实轴长为2
B.双曲线C的焦点到渐近线的距离为m
C.若(2,0)是双曲线C的一个焦点,则m=2
D.若双曲线C的两条渐近线相互垂直,则m=2
(多选)11.(2025春 望城区校级期末)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点,若∠ABD=90°,且△ABF的面积为,则( )
A.|BF|=4
B.△ABF是等边三角形
C.△BDF的面积为
D.抛物线C的方程为y2=4x
三.填空题(共3小题)
12.(2025春 甘肃月考)已知椭圆的左、右焦点分别为F1,F2,过F1作斜率为的直线l交E于第一象限的点A,则△AF1F2外接圆的半径为 .
13.(2025春 崂山区校级期中)已知直线l过双曲线的右焦点,且与双曲线交于A,B两点,则|AB|的最小值为 .
14.(2025春 集宁区校级期中)已知抛物线的方程为y2=4x,过其焦点F的直线交此抛物线于M、N两点,交y轴于点E,若,,则λ1+λ2= .
四.解答题(共5小题)
15.(2025春 科左中旗校级期末)已知焦点位于x轴的抛物线C过点M(1,2).
(1)求抛物线C的方程,并求其准线方程;
(2)过该抛物线的焦点,作倾斜角为60°的直线,交抛物线于A,B两点,求线段AB的长度.
16.(2024秋 南开区校级期末)设椭圆,且离心率为,过点P(4,0)的直线与椭圆交于A,B两点,当直线AB经过椭圆中心O时,|AB|=4.
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知点T(1,1),直线AT和直线BT分别与y轴交于C,D,与x轴交于E,F,若3S△CDT=S△EFT,求直线AB的斜率.
17.(2024秋 杨浦区校级期末)已知过点的双曲线C的渐近线方程为.如图所示,过双曲线C的右焦点F作与坐标轴都不垂直的直线l交C的右支于A,B两点.
(1)求双曲线C的标准方程;
(2)若双曲线C上的点Q(x0,y0)到其两条渐近线的距离分别为d1,d2,求d1d2的值;
(3)已知点,求证:∠AQF=∠BQF.
18.(2025春 丽水月考)已知椭圆Γ的方程为,椭圆Γ的左、右焦点分别为F1、F2,过F2的直线l与椭圆Γ交于P、Q两点(P、Q均不在x轴上).
(1)若椭圆Γ的离心率为,求a的值;
(2)若a=2,左顶点为A,求△APQ的面积的最大值.
19.(2025春 峨山县校级期末)已知直线l:y=kx+b与圆O:x2+y2=1相切.
(1)求k2﹣b2的值;
(2)已知椭圆E:在点P(x0,y0)处的切线方程为,若直线l与椭圆E相交于A,B两点,分别过A,B作椭圆E的切线,两条切线相交于点Q,求点Q的轨迹方程;
(3)是否存在这样的二次曲线F:λx2+μy2=1,当直线l与曲线F有两个交点M,N时,总有OM⊥ON?若存在,求出λ+μ的值;若不存在,请说明理由.
第三章圆锥曲线的方程检测卷-2025-2026学年高二数学上学期人教A版2019选择性必修第一册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A B D C D A A D
二.多选题(共3小题)
题号 9 10 11
答案 BD CD ABD
一.选择题(共8小题)
1.(2025春 新化县校级月考)抛物线y=﹣5x2的准线方程为( )
A. B. C. D.
【解答】解:由题可得抛物线方程为:,
2p,且开口向下,
所以抛物线y=﹣5x2的准线方程为.
故选:A.
2.(2026春 江汉区月考)已知双曲线,则C的右焦点到其渐近线的距离为( )
A.2 B.6 C. D.
【解答】解:双曲线,
a2=4,b2=36,∴,
∴右焦点坐标为,其中一条渐近线方程为y=3x,
∴右焦点到其渐近线的距离为.
故选:B.
3.(2024秋 朝阳校级期末)已知抛物线C:y2=2x,过点的直线l与C相交于A,B两点,且M为弦AB的中点,则直线l的方程为( )
A.6x+6y﹣7=0 B.6x﹣6y﹣1=0
C.2x﹣6y﹣5=0 D.12x﹣6y﹣5=0
【解答】解:已知抛物线C:y2=2x,过点的直线l与C相交于A,B两点,且M为弦AB的中点,
显然直线l不垂直于y,设直线l的方程为,
由,
消去x得,
由弦AB的中点为,
得,
此时方程有两个不等实根,
所以直线l的方程为,
即直线l的方程为12x﹣6y﹣5=0.
故选:D.
4.(2024秋 安徽期末)已知椭圆的左、右焦点分别为F1,F2,且椭圆上存在点P,使得|PF1|=7|PF2|,则该椭圆的离心率的取值范围是( )
A. B. C. D.
【解答】解:由椭圆的定义得|PF1|+|PF2|=2a,又|PF1|=7|PF2|,所以,
又a﹣c≤|PF1|≤a+c,a﹣c≤|PF2|≤a+c,
所以a≤a+c,且a﹣ca,所以,即,
即椭圆的离心率的取值范围是.
故选:C.
5.(2025 保山校级一模)双曲线的左、右焦点分别为F1、F2.过F2作其中一条渐近线的垂线,垂足为P.已知PF2=2,直线PF1的斜率为,则双曲线的方程为( )
A. B.1
C. D.
【解答】解:根据对称性,不妨设双曲线的其中一条渐近线方程为,
则过F2(c,0)且垂直渐近线的直线方程为,
联立,可得P(,),
∴|PF2|b=2,又F1(﹣c,0),
∴,∴,
∴,∴a,又b=2,
∴双曲线的方程为.
故选:D.
6.(2025 临翔区校级模拟)已知双曲线E的右焦点为F,以F为圆心,为半径的圆与双曲线E的一条渐近线交于A,B两点,若,则双曲线E的离心率为( )
A. B. C. D.3
【解答】解:令点F(c,0),双曲线E 的渐近线方程为,
由对称性不妨取直线AB:bx﹣ay=0,取AB中点C,连接FC,则FC⊥AB,
,而,
由,得|OC|=|AB|=2b,在Rt△OCF中,c2=(2b)2+b2=5b2,
则a2=c2﹣b2=4b2,解得,
所以双曲线 E的离心率.
故选:A.
7.(2025春 张掖月考)已知平行四边形ABCD内接于椭圆Ω:,且AB,AD斜率之积的范围为,则椭圆Ω离心率的取值范围是( )
A. B.
C. D.
【解答】解:已知平行四边形ABCD内接于椭圆Ω:,
且AB,AD斜率之积的范围为,
则A,C和B,D均关于原点对称,令B(m,n),则D(﹣m,﹣n),
若A(x,y),则,
所以椭圆Ω离心率.
故选:A.
8.(2024秋 清远期末)已知双曲线C:的离心率为,右焦点F到其渐近线的距离为,过F的直线与C的右支交于P,Q两点(P在Q的上方),PQ的中点为M,M在直线l:x=2上的射影为N,O为坐标原点,设△POQ的面积为S,直线PN,QN的斜率分别为k1,k2,则( )
A.2 B. C.1 D.
【解答】解:∵双曲线C:的离心率为,右焦点F到其渐近线的距离为,
∴由题知,解得,
∴双曲线C:,∴F(3,0),
依题意可设PQ:x=my+3,
代入双曲线C:,消去x,整理得(m2﹣2)y2+6my+3=0,
设P(x1,y1),Q(x2,y2),y1>y2,
则,又M(,),N(2,),
∴k1﹣k2,
∵S|OF| (y1﹣y2)(y1﹣y2),
∴.
故选:D.
二.多选题(共3小题)
(多选)9.(2025春 揭阳月考)以两条直线5x±3y﹣2=0为渐近线的双曲线的离心率可以是( )
A. B. C. D.
【解答】解:根据渐近线方程5x±3y﹣2=0可得,双曲线的渐近线斜率为.
根据双曲线渐近线方程的性质可得或.
①当时,,
∴,则
②当时,,
∴,则,
∴以两条直线5x±3y﹣2=0为渐近线的双曲线的离心率可以是或.
故选:BD.
(多选)10.(2024秋 厦门校级期末)已知双曲线C:,则下列说法正确的是( )
A.双曲线C的实轴长为2
B.双曲线C的焦点到渐近线的距离为m
C.若(2,0)是双曲线C的一个焦点,则m=2
D.若双曲线C的两条渐近线相互垂直,则m=2
【解答】解:∵曲线C:为双曲线,
∴m>0,且a,b,则双曲线C的实轴长为2,故A错误;
取双曲线一个焦点F(c,0),一条渐近线方程为y,即bx﹣ay=0,
则双曲线C的焦点到渐近线的距离为,故B错误;
若(2,0)是双曲线C的一个焦点,则2+m=4,得m=2,故C正确;
若双曲线C的两条渐近线相互垂直,则,即m=2,故D正确.
故选:CD.
(多选)11.(2025春 望城区校级期末)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点,若∠ABD=90°,且△ABF的面积为,则( )
A.|BF|=4
B.△ABF是等边三角形
C.△BDF的面积为
D.抛物线C的方程为y2=4x
【解答】解:抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点,
设准线l与x轴交于点M,如图,
抛物线定义知|AB|=|AF|,又|BF|=|AF|,所以△ABF为正三角形,故B正确;
由△ABF面积为知△ABF边长|BF|=4,故A正确;
则由直角三角形MBF可得p=2|OF|=|MF|=4cos60°=2,
所以抛物线C的方程为y2=4x,故D正确;
△BDF面积为,故C错误.
故选:ABD.
三.填空题(共3小题)
12.(2025春 甘肃月考)已知椭圆的左、右焦点分别为F1,F2,过F1作斜率为的直线l交E于第一象限的点A,则△AF1F2外接圆的半径为 .
【解答】解:已知椭圆的左、右焦点分别为F1,F2,过F1作斜率为的直线l交E于第一象限的点A,
因为∠AF1F2∈(0,π),且,
解得,,
又,
设|AF2|=t,则|AF1|=6﹣t,
由余弦定理知,
即,
解得t=2,
即|AF2|=2,|AF1|=4,
则易知AF2⊥l,
故,
即△AF1F2的外接圆半径为.
故答案为:.
13.(2025春 崂山区校级期中)已知直线l过双曲线的右焦点,且与双曲线交于A,B两点,则|AB|的最小值为 5 .
【解答】解:在双曲线C:中,a2=4,b2=5,则,所以右焦点坐标为(3,0),
当直线l垂直于x轴时,直线l与双曲线的交点A、B的横坐标都为3,
将x=3代入双曲线方程,可得,解得,
此时;
当直线l不垂直于x轴时,设直线l的方程为y=k(x﹣3),A(x1,y1),B(x2,y2),
将y=k(x﹣3)代入双曲线方程,整理可得(5﹣4k2)x2+24k2x﹣36k2﹣20=0,
Δ=(24k2)2﹣4×(5﹣4k2)×(﹣36k2﹣20)=400k2+400>0,
由韦达定理可知,,
则|AB|
|5|>5,
所以|AB|的最小值为5.
故答案为:5.
14.(2025春 集宁区校级期中)已知抛物线的方程为y2=4x,过其焦点F的直线交此抛物线于M、N两点,交y轴于点E,若,,则λ1+λ2= ﹣1 .
【解答】解:由抛物线的方程为y2=4x,
得F(1,0),
由题意可得直线MN的斜率存在且不等于零,
则可设直线MN的方程为x=my+1(m≠0),M(x1,y1),N(x2,y2),
联立,
消x得y2﹣4my﹣4=0,
则Δ=16m2+16>0恒成立,
则y1+y2=4m,y1y2=﹣4,
故,
由直线x=my+1(m≠0),
令x=0,
得,
则,
由,
得,
所以x1=λ1(1﹣x1),
所以,
由,
得,
所以x2=λ2(1﹣x2),
所以,
所以
.
故答案为:﹣1.
四.解答题(共5小题)
15.(2025春 科左中旗校级期末)已知焦点位于x轴的抛物线C过点M(1,2).
(1)求抛物线C的方程,并求其准线方程;
(2)过该抛物线的焦点,作倾斜角为60°的直线,交抛物线于A,B两点,求线段AB的长度.
【解答】解:(1)由题意可知,抛物线C的焦点位于x轴正半轴,
设抛物线C的方程为y2=2px(p>0),
因为抛物线C过点M(1,2),
所以2p=4,解得p=2,
故抛物线C的方程为y2=4x,其准线方程为x=﹣1.
(2)由(1)知,抛物线C的焦点为F(1,0),
因为直线AB的倾斜角为60°,且过抛物线C的焦点F,
所以直线AB的方程为,
由,得3x2﹣10x+3=0,
设A(x1,y1),B(x2,y2),则,
所以.
16.(2024秋 南开区校级期末)设椭圆,且离心率为,过点P(4,0)的直线与椭圆交于A,B两点,当直线AB经过椭圆中心O时,|AB|=4.
(Ⅰ)求椭圆M的方程;
(Ⅱ)已知点T(1,1),直线AT和直线BT分别与y轴交于C,D,与x轴交于E,F,若3S△CDT=S△EFT,求直线AB的斜率.
【解答】解:(Ⅰ)当直线AB经过椭圆中心O时,可知|AB|=2a=4,所以a=2,
又因为离心率,因此,所以b2=a2﹣c2=1,
因此椭圆方程;
(Ⅱ)①当直线AB的方程为y=0时,易知B(2,0),A(﹣2,0);
直线BT的方程为y=﹣x+2,因此D(0,2);
直线AT的方程为,因此;
此时点点F与点B重合,E与点A重合,易知3S△CDT=S△EFT;
②设直线AB为x=my+4,B(x2,y2),A(x1,y1),
所以,
根的判别式Δ=64m2﹣48(m2+4)>0,解得m2﹣12>0,
所以或,且;
所以根据韦达定理可得,,
所以,,
所以3S△CDT=S△EFT 3CD=EF 3|yC﹣yD|=|xE﹣xF|
直线,直线,
令y=0,,,
令x=0,,,
所以
所以|x1x2﹣(x1+x2)+1|=3|y1y2﹣(y1+y2)+1|,
所以|﹣4m2+64﹣32+m2+4|=3|12+8m+m2+4|,
即|﹣3m2+36|=3|m2+8m+16|.
所以24m+84=0,解得,斜率为;
综上所述,直线AB的斜率为0或.
17.(2024秋 杨浦区校级期末)已知过点的双曲线C的渐近线方程为.如图所示,过双曲线C的右焦点F作与坐标轴都不垂直的直线l交C的右支于A,B两点.
(1)求双曲线C的标准方程;
(2)若双曲线C上的点Q(x0,y0)到其两条渐近线的距离分别为d1,d2,求d1d2的值;
(3)已知点,求证:∠AQF=∠BQF.
【解答】解:(1)因为双曲线C的渐近线方程为,
所以设双曲线方程为x2﹣3y2=λ(λ≠0),
又双曲线过点,
则λ=9﹣3×2=3,所以双曲线的方程为x2﹣3y2=3,
即.
(2)因为Q(x0,y0)在曲线上,
则,
渐近线方程:,
所以.
(3)证明:由(1)可知F(2,0),l的斜率存在且不为0,设l的方程为y=k(x﹣2),
联立,消去y得(1﹣3k2)x2+12k2x﹣12k2﹣3=0,
设A(x1,y1),B(x2,y2),由题意得,
则,
所以
,
所以kAQ=﹣kBQ,∠AQF=∠BQF得证.
18.(2025春 丽水月考)已知椭圆Γ的方程为,椭圆Γ的左、右焦点分别为F1、F2,过F2的直线l与椭圆Γ交于P、Q两点(P、Q均不在x轴上).
(1)若椭圆Γ的离心率为,求a的值;
(2)若a=2,左顶点为A,求△APQ的面积的最大值.
【解答】解:(1)因为椭圆Γ的离心率为,
因此,
解得.
(2)a=2时,c2=a2﹣1=3,故,因此,,
P、Q均不在x轴上,故直线l的斜率不为0,
设直线l的方程为,P(x1,y1),Q(x2,y2),
联立与得,
因Δ=12m2+4(m2+4)=16m2+16>0,
由韦达定理,,,
因此,
代入,,原式得,
又,故△APQ的面积,
而,
当且仅当,即m2=2时等号成立,
因此△APQ的面积的最大值为.
19.(2025春 峨山县校级期末)已知直线l:y=kx+b与圆O:x2+y2=1相切.
(1)求k2﹣b2的值;
(2)已知椭圆E:在点P(x0,y0)处的切线方程为,若直线l与椭圆E相交于A,B两点,分别过A,B作椭圆E的切线,两条切线相交于点Q,求点Q的轨迹方程;
(3)是否存在这样的二次曲线F:λx2+μy2=1,当直线l与曲线F有两个交点M,N时,总有OM⊥ON?若存在,求出λ+μ的值;若不存在,请说明理由.
【解答】解:(1)因为直线l与圆O相切,
所以圆心O到直线l的距离,
则k2﹣b2=﹣1;
(2)设A(x1,y1),B(x2,y2),Q(x0,y0),
可得椭圆E在点A(x1,y1)处的切线AQ方程为,
因为点Q(x0,y0)在切线AQ上,
所以,①
同理得,②
由①②得A(x1,y1),B(x2,y2)都在直线上,
所以直线AB方程为,③
因为圆O与直线AB相切,
所以点O到直线AB的距离,
所以,
因为点Q(x0,y0)具有任意性,
则点Q的轨迹方程为;
(3)假设存在曲线F满足条件,设M(x3,y3),N(x4,y4),
联立,消去y并整理得(λ+μk2)x2+2kbμy+μb2﹣1=0,
此时Δ>0,
由韦达定理得.
因为OM⊥ON,
所以
恒成立.
故所以存在曲线F,且λ+μ=1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
