1.2.3 相反数 课件(共14张PPT)
文档属性
| 名称 | 1.2.3 相反数 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 22:29:04 | ||
图片预览




文档简介
(共14张PPT)
第一章 有理数
1.2.3 相反数
学习目标:
1. 能说出相反数的意义.
2. 知道求一个已知数的相反数的方法.
3. 能运用数形结合思想理解相反数的几何意义.
学习重、难点:
重点: 说出相反数的意义,体会相反数的代数意义与几何意义的一致性.
难点: 归纳相反数在数轴上所表示的点的位置特征.
思
考
1. 数轴上与原点的距离是2的点有 个,这些点表示的数是 ;
2. 数轴上与原点的距离是5的点有 个,这些点表示的数是 ;
3. 数轴上与原点的距离是3.5的点有 个,这些点表示的数是 。
两
两
两
﹢2和﹣2
﹢5和﹣5
﹢3.5和﹣3.5
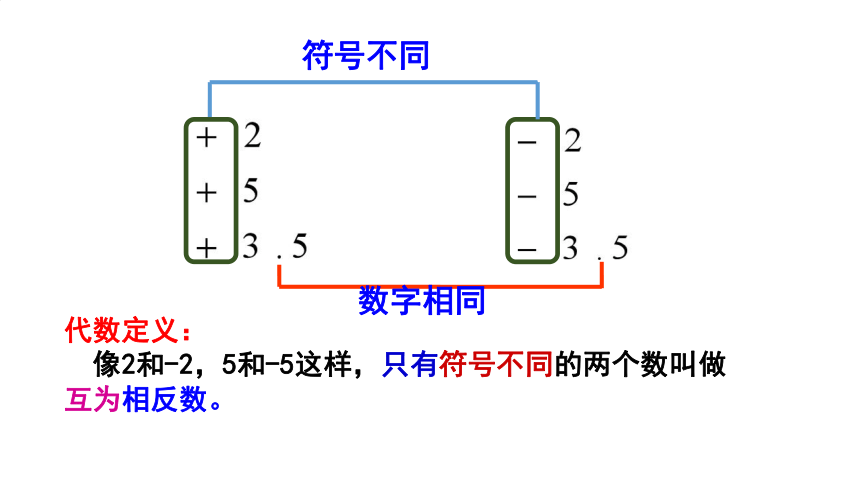
数字相同
符号不同
代数定义:
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数。
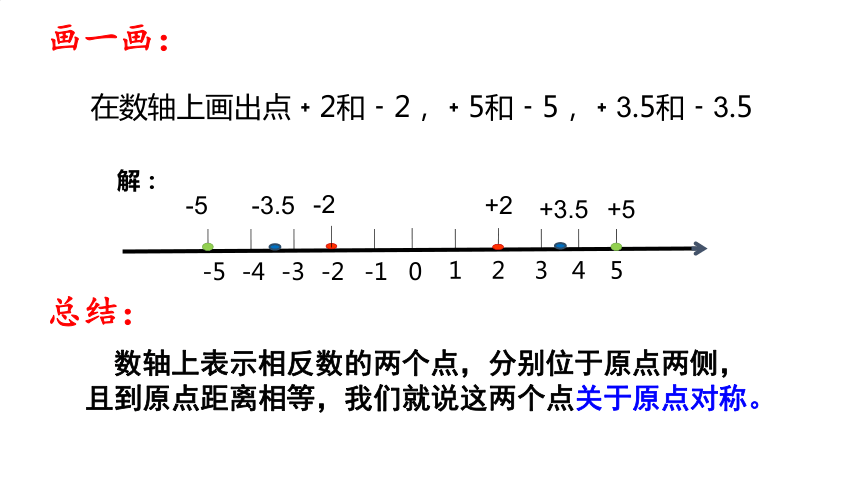
数轴上表示相反数的两个点,分别位于原点两侧,且到原点距离相等,我们就说这两个点关于原点对称。
在数轴上画出点﹢2和﹣2,﹢5和﹣5,﹢3.5和﹣3.5
画一画:
0
1
2
3
解:
4
5
-5
-4
-3
-2
-1
+5
-5
总结:
-2
+2
-3.5
+3.5
0
1
2
3
解:
4
5
-5
-4
-3
-2
-1
+5
-5
-2
+2
-3.5
+3.5
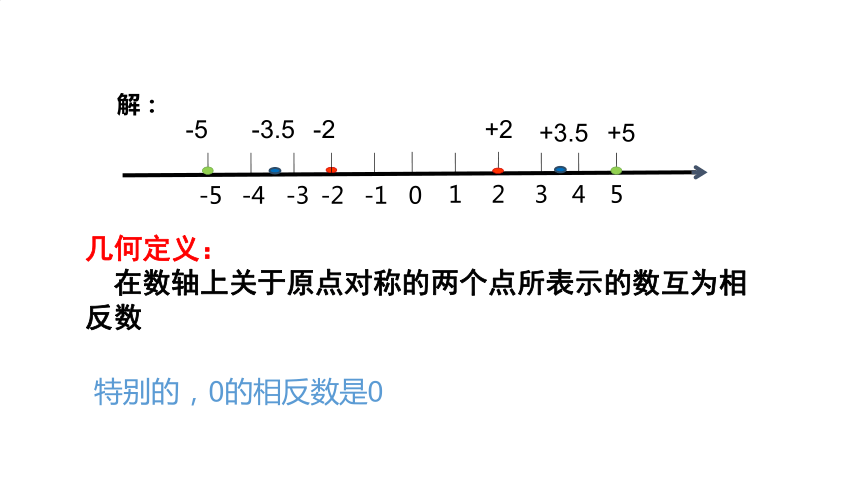
几何定义:
在数轴上关于原点对称的两个点所表示的数互为相反数
特别的,0的相反数是0
用相反数化简
如何进行符号化简呢?你能自己总结出简化符号的规律吗?
简化符号:
-(-6)=______; +(-6)=________;
-(+0.73)=_______;-0=________;
-(-34)=________; -(- ) ________.
如何进行符号化简呢?你能自己总结出简化符号的规律吗?
方法总结:
对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.如果有奇数个“-”号,结果的符号就是“-”号;如果有偶数个“-”号,结果的符号就是“+”号
练习 教科书第10页
1.判断下列说法是否正确:
(1)-3是相反数; (2)+3是相反数;
(3)3是-3的相反数;(4)-3与+3互为相反数.
2. 写出下列各数的相反数:
6,-8,-3.9, , ,100 ,0 .
3.如果a=-a,那么表示a的点在数轴上的什么位置?
原点位置
思维导图:
拓展探究
多重符号的化简
问题1:利用相反数的定义化简下列各数:
(1)-(+10) ; (2)+(-0.15); (3)+(+3); (4)-(-12) .
(2)-[+(-7)]=-(-7)=7.
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
解:(1)+[-(-1.1)]=+(+1.1)=1.1;
问题2:类比问题1,你能化简下列各数吗?(1)+[-(-1.1)] ;(1)-[+(-7)].
答:化简多重符号时,凡是“+”都去掉,结果的符号取决于数字前面有多少个负号:
若有偶数个,则结果为正;
若有奇数个,则结果为负.
问题3:根据上述化简结果,你认为该如何进行多重符号的化简?
口诀
一查二定
作业:
练习4 如果a与b互为相反数,则a+b+3=————?
练习5 写出下列各数的相反数,并将这些数同他们的相反数在数轴上表示出来。
第一章 有理数
1.2.3 相反数
学习目标:
1. 能说出相反数的意义.
2. 知道求一个已知数的相反数的方法.
3. 能运用数形结合思想理解相反数的几何意义.
学习重、难点:
重点: 说出相反数的意义,体会相反数的代数意义与几何意义的一致性.
难点: 归纳相反数在数轴上所表示的点的位置特征.
思
考
1. 数轴上与原点的距离是2的点有 个,这些点表示的数是 ;
2. 数轴上与原点的距离是5的点有 个,这些点表示的数是 ;
3. 数轴上与原点的距离是3.5的点有 个,这些点表示的数是 。
两
两
两
﹢2和﹣2
﹢5和﹣5
﹢3.5和﹣3.5
数字相同
符号不同
代数定义:
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数。
数轴上表示相反数的两个点,分别位于原点两侧,且到原点距离相等,我们就说这两个点关于原点对称。
在数轴上画出点﹢2和﹣2,﹢5和﹣5,﹢3.5和﹣3.5
画一画:
0
1
2
3
解:
4
5
-5
-4
-3
-2
-1
+5
-5
总结:
-2
+2
-3.5
+3.5
0
1
2
3
解:
4
5
-5
-4
-3
-2
-1
+5
-5
-2
+2
-3.5
+3.5
几何定义:
在数轴上关于原点对称的两个点所表示的数互为相反数
特别的,0的相反数是0
用相反数化简
如何进行符号化简呢?你能自己总结出简化符号的规律吗?
简化符号:
-(-6)=______; +(-6)=________;
-(+0.73)=_______;-0=________;
-(-34)=________; -(- ) ________.
如何进行符号化简呢?你能自己总结出简化符号的规律吗?
方法总结:
对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.如果有奇数个“-”号,结果的符号就是“-”号;如果有偶数个“-”号,结果的符号就是“+”号
练习 教科书第10页
1.判断下列说法是否正确:
(1)-3是相反数; (2)+3是相反数;
(3)3是-3的相反数;(4)-3与+3互为相反数.
2. 写出下列各数的相反数:
6,-8,-3.9, , ,100 ,0 .
3.如果a=-a,那么表示a的点在数轴上的什么位置?
原点位置
思维导图:
拓展探究
多重符号的化简
问题1:利用相反数的定义化简下列各数:
(1)-(+10) ; (2)+(-0.15); (3)+(+3); (4)-(-12) .
(2)-[+(-7)]=-(-7)=7.
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
解:(1)+[-(-1.1)]=+(+1.1)=1.1;
问题2:类比问题1,你能化简下列各数吗?(1)+[-(-1.1)] ;(1)-[+(-7)].
答:化简多重符号时,凡是“+”都去掉,结果的符号取决于数字前面有多少个负号:
若有偶数个,则结果为正;
若有奇数个,则结果为负.
问题3:根据上述化简结果,你认为该如何进行多重符号的化简?
口诀
一查二定
作业:
练习4 如果a与b互为相反数,则a+b+3=————?
练习5 写出下列各数的相反数,并将这些数同他们的相反数在数轴上表示出来。
同课章节目录
