1.2.4 绝对值 课件(共16张PPT)
文档属性
| 名称 | 1.2.4 绝对值 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 22:28:35 | ||
图片预览





文档简介
(共16张PPT)
1.2.4 绝对值
人教版·七年级上册
学习目标
1. 知道绝对值的概念及表示法,体会绝对值
的几何意义.
2.会求一个已知数的绝对值.
新课导入
-1 和 1,-2 和 2,-3 和 3,…
我们知道,互为相反数的两个数(除 0 以外)只有符号不同. 这两个数的相同部分在数轴上表示什么?
观察
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处.
它们行驶的路线相同吗?
它们行驶的路程相同吗?
不同,因为方向不同.
因为,线段OA的长度 = 线段OB的长度
O
B
A
0
10
-10
10
10
相同.
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
A, B两点分别表示数-10和10,它们与原点的距离都是10个单位长度,所以-10和10的绝对值都是10,即 |-10|=10,|10|=10.
显然|0|=0.
这里的数a可以是正数、负数和0
概念
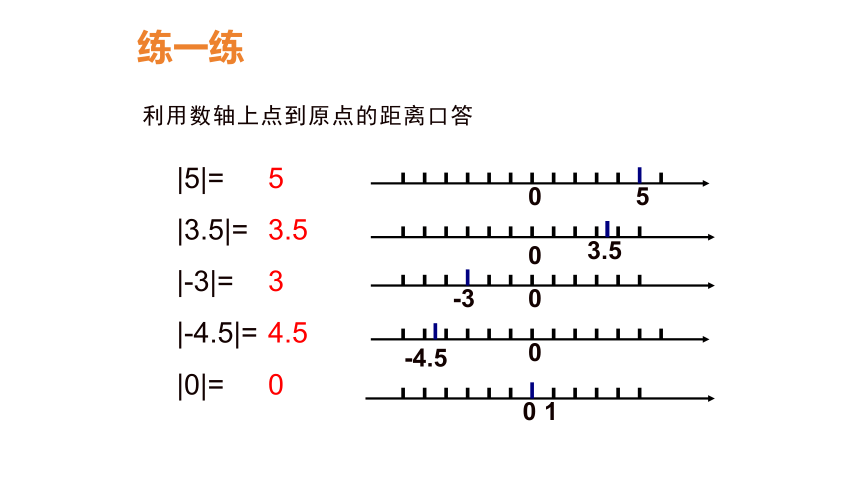
利用数轴上点到原点的距离口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
1
0
0
0
0
5
3.5
-3
-4.5
5
3.5
3
4.5
0
练一练
例题
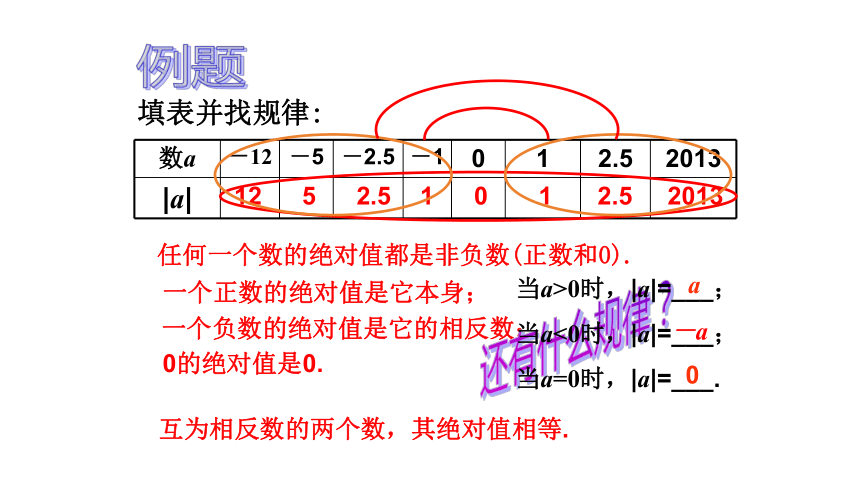
填表并找规律:
数a -12 -5 -2.5 -1 0 1 2.5 2013
|a|
12
5
2.5
1
1
0
2.5
2013
任何一个数的绝对值都是非负数(正数和0).
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0.
还有什么规律?
互为相反数的两个数,其绝对值相等.
当a>0时,|a|=___;
当a<0时,|a|=___;
当a=0时,|a|=___.
a
-a
0
小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有|a| ≥0.
归纳:
深化理解
例 (1)分别写出 1, -0.5 和 的绝对值;
【教材P13】
例 题
| 1 | = 1;
0
1
2
-1
-2
距离为1
距离为0.5
距离为
|-0.5| = 0.5;
(2)因为在点 A,B,C,D 中,点 C 离原点最近,所以在有理数 a,b,c,d 中,c 的绝对值最小.
(2)如图,数轴上的点 A,B,C,D 分别表示有理数a,b,c,d,这四个数中,绝对值最小的是哪个数?
0
1
2
3
-1
-2
-3
4
-4
A
B
C
D
巩固训练
表示 +7 的点与原点的距离是______;
即:+7 的绝对值是______,记作__________;
表示 -2.8 的点与原点的距离是________;
即:-2.8 的绝对值是______,记作___________;
表示 0 的点与原点的距离是________;
即:0 的绝对值是______,记作_________.
7
7
| +7 | = 7
2.8
2.8
| -2.8 | = 2.8
0
0
| 0 | = 0
归 纳
求一个数的绝对值的方法:
求一个数的绝对值
正数
0
负数
等于它本身
等于它的相反数
1.写出下列各数的绝对值:
新课本练习
2.判断题.
(1)绝对值是它本身的数是正数;
(2)当a≠0时,|a|总是大于0;
(3)绝对值小于2的数是1和-1.
正数和0
√
0、1和-1
3.如果|a|=|-2|,那么a= ;如果m是负数,且|m|=10,那么m= .
±2
-10
新课本练习
4.化简下列各数:
新课本练习
课堂小结
一般地,数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值,记作 |a|.
(1)若 a > 0,则 | a | = a;
(2)若 a = 0,则 | a | = 0;
(3)若 a < 0,则 | a | =-a.
1.2.4 绝对值
人教版·七年级上册
学习目标
1. 知道绝对值的概念及表示法,体会绝对值
的几何意义.
2.会求一个已知数的绝对值.
新课导入
-1 和 1,-2 和 2,-3 和 3,…
我们知道,互为相反数的两个数(除 0 以外)只有符号不同. 这两个数的相同部分在数轴上表示什么?
观察
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处.
它们行驶的路线相同吗?
它们行驶的路程相同吗?
不同,因为方向不同.
因为,线段OA的长度 = 线段OB的长度
O
B
A
0
10
-10
10
10
相同.
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
A, B两点分别表示数-10和10,它们与原点的距离都是10个单位长度,所以-10和10的绝对值都是10,即 |-10|=10,|10|=10.
显然|0|=0.
这里的数a可以是正数、负数和0
概念
利用数轴上点到原点的距离口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
1
0
0
0
0
5
3.5
-3
-4.5
5
3.5
3
4.5
0
练一练
例题
填表并找规律:
数a -12 -5 -2.5 -1 0 1 2.5 2013
|a|
12
5
2.5
1
1
0
2.5
2013
任何一个数的绝对值都是非负数(正数和0).
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0.
还有什么规律?
互为相反数的两个数,其绝对值相等.
当a>0时,|a|=___;
当a<0时,|a|=___;
当a=0时,|a|=___.
a
-a
0
小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有|a| ≥0.
归纳:
深化理解
例 (1)分别写出 1, -0.5 和 的绝对值;
【教材P13】
例 题
| 1 | = 1;
0
1
2
-1
-2
距离为1
距离为0.5
距离为
|-0.5| = 0.5;
(2)因为在点 A,B,C,D 中,点 C 离原点最近,所以在有理数 a,b,c,d 中,c 的绝对值最小.
(2)如图,数轴上的点 A,B,C,D 分别表示有理数a,b,c,d,这四个数中,绝对值最小的是哪个数?
0
1
2
3
-1
-2
-3
4
-4
A
B
C
D
巩固训练
表示 +7 的点与原点的距离是______;
即:+7 的绝对值是______,记作__________;
表示 -2.8 的点与原点的距离是________;
即:-2.8 的绝对值是______,记作___________;
表示 0 的点与原点的距离是________;
即:0 的绝对值是______,记作_________.
7
7
| +7 | = 7
2.8
2.8
| -2.8 | = 2.8
0
0
| 0 | = 0
归 纳
求一个数的绝对值的方法:
求一个数的绝对值
正数
0
负数
等于它本身
等于它的相反数
1.写出下列各数的绝对值:
新课本练习
2.判断题.
(1)绝对值是它本身的数是正数;
(2)当a≠0时,|a|总是大于0;
(3)绝对值小于2的数是1和-1.
正数和0
√
0、1和-1
3.如果|a|=|-2|,那么a= ;如果m是负数,且|m|=10,那么m= .
±2
-10
新课本练习
4.化简下列各数:
新课本练习
课堂小结
一般地,数轴上表示数 a 的点与原点的距离叫作数 a 的绝对值,记作 |a|.
(1)若 a > 0,则 | a | = a;
(2)若 a = 0,则 | a | = 0;
(3)若 a < 0,则 | a | =-a.
同课章节目录
