1.1 相似多边形 课件(共24张PPT) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 1.1 相似多边形 课件(共24张PPT) 2025-2026学年数学青岛版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:32:02 | ||
图片预览







文档简介
(共24张PPT)
第1章 图形的相似
九年级上册
1.1 相似多边形
课前小测
1.什么叫做全等三角形 它的形状、大小有何特征
能够安全重合的两个三角形叫全等三角形;
它们的形状相同,大小相等.
2.两个全等三角形的对应边和对应角有什么关系
对应边相等,对应角相等.
情境引入
问题:五星红旗是中华人民共和国的国旗,国旗上五颗星星形状相同吗?大小相等吗?
情境引入
形状相同,大小不相等.
情境引入
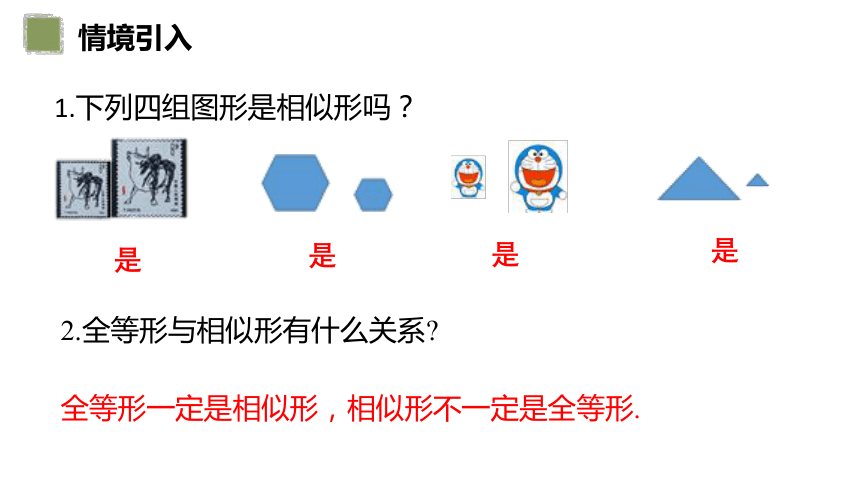
1.下列四组图形是相似形吗?
是
2.全等形与相似形有什么关系
全等形一定是相似形,相似形不一定是全等形.
是
是
是
情境引入
形状相同是对相似形的一种描述,你能利用两个相似多边形的各角之间及各边之间的数量关系表述它们形状相同的特征吗
合作探究
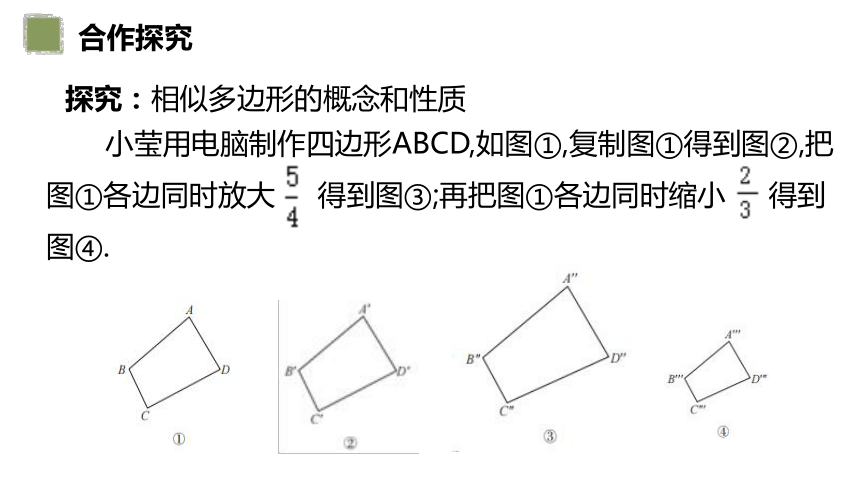
探究:相似多边形的概念和性质
小莹用电脑制作四边形ABCD,如图①,复制图①得到图②,把图①各边同时放大 得到图③;再把图①各边同时缩小 得到图④.
观察得到的四个四边形,你发现它们的形状和大小有什么特征 它们是相似形吗
形状相同,大小不同.它们是相似形.
合作探究
探究:相似多边形的概念和性质
合作探究
探究:相似多边形的概念和性质
(2)观察图①和图③,相应的角之间有怎样的数量关系 相应的各边的比之间有怎样的关系
,即对应边的比相等.
∠A= ∠ A‘’ ,∠ B= ∠ B ‘’,∠ C =∠ C‘’ ,∠ D =∠ D‘’,即对应角相等.
合作探究
探究:相似多边形的概念和性质
(3)观察图①和图④,相应的各角及相应的各边分别具有怎样的数量关系 图③和图④呢
③和④也是对应角相等,对应边的比值相等.
①和④对应角相等. ∠A= ∠ A''' ,∠ B= ∠ B ″′,∠ C =∠ C′′′,∠ D =∠ D'″
合作交流
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角相等,各边对应成比例,那么这两个多边形叫做相似多边形.
记法:四边形ABCD∽四边形A ′ B ′ C ′ D ′ .
读作:四边形ABCD“相似于”四边形A ′ B ′ C ′ D ′ .
相似比:相似多边形对应边的比叫做相似比.
相似多边形的性质:如果两个多边形相似,那么它们的对应角相等,对应边成比例.
定义:
合作探究
注意:
(1)对应顶点的字母写在对应的位置上.
(3)如果两个相似多边形相似比为1,那么这两个多边形全等.
(2)相似比是有顺序的.若正方形ABCD与正方形A1B1C1D1 的相似比为5:4,则正方A1B1C1D1与正方形ABCD的相似比为 .
4∶5
[例1]
下列说法正确的是( )
A.菱形都相似
B.正六边形都相似
C.矩形都相似
D.含80°角的等腰三角形都相似
B
典例分析
典例分析
解析:A.因为菱形的四条边相等,所以所有菱形的边对应成比例,但角不一定对应相等,所以菱 形不一定都相似,故本选项说法错误; B.因为正六边形的六条边相等,所以所有正六边形的边对应成比例,又因为正六边形的内 角都是120°,即角对应相等,所以正六边形都相似,故本选项说法正确;
C.因为矩形的内角都是90°,但边不一定对应成比例,所以矩形不一定都相似,故本选项中说法错误;
D.含80°角的等腰三角形,可能顶角是80°,也可能底角是80°,无法判定这样的等腰三角形相似,故本选项说法错误.
典例分析
[例2]
如图,四边形AEFD∽四边形EBCF.
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长.
解:(1)∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC,
(2)∵AD=3,EF=4且
,
,解得
.
.
∴
有两个多边形的各个角分别相等,能断定它们相似吗 由两个多边形的边对应成比例,能断定它们相似吗 如果不能,请分别举出反例;如果能,说明你的理由.
拓展
答:由两个多边形的各个角分别相等,不能断定他们相似,例如正方形和矩形,各个角分别相等但不相似.有两个多边形的边对应成比例,不能断定他们相似,例如正方形和菱形,各边对应成比例但不相似.
试一试
如图,已知△AOB∽△COD,∠A=∠C,则下列各式正确的有( )
A
B
O
C
D
A.1个 B.2个 C.3个 D.4个
A
归纳小结
1.相似多边形的定义
3.相似比
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角相等,各边对应成比例,那么这两个多边形叫做相似多边形.
2.相似多边形的性质
相似多边形对应边的比叫做相似比.
如果两个相似多边形相似比为1,那么这两个多边形全等.
如果两个多边形相似,那么它们的对应角相等,对应边成比例.
随堂检测
相似多边形课堂评价测试
同学们要认真答题哦!
随堂检测
1.下列四组图形中,不是相似形的是( )
B.
C.
D.
2.下列结论正确的有( )
(1)所有圆都相似;(2)所有正方形都相似;
(3)所有等腰三角形都相似;(4)所有矩形都相似.
A.1个 B.2个 C.3个 D.4个
3. 把一个长方形按如图所示的方式划分成三个全等的小长方形,每一个小长方形与原长方形相似,若小长方形的宽为2,则原长方形的宽x为______.
2
x
D
B
A.
随堂检测
4.两个相似多边形的相似比是3∶7,其中一个多边形的最长边是21, 则另一个多边形的最长边是________.
5.如图,菱形ABCD边长为3,∠B=60°,菱形A B C D 边长为5,∠C =120°,这两个菱形相似吗?试说明理由.
A
B
C
D
A'
B'
C'
D'
解:相似.理由如下:
∵四边形ABCD是菱形, ∠B=60 °,
∴∠A=120 °, ∠C=120 °, ∠D=60° .
∵四边形A B C D 是菱形,∠C =120° ,
∴∠A =120° , ∠B =60° , ∠D =60°,
∴∠A=∠A , ∠B= ∠B , ∠C= C , ∠D= ∠D ,
∴这两个菱形相似.
49或9
,
课堂小结
1.说一说相似形的定义;相似与全等的关系.
关系:全等形一定是相似形,相似形不一定是全等形.
2.相似多边形的概念、表示方法,相似比的定义是什么?
如果两个相似多边形的相似比为1,那么这两个多边形全等.
3.相似多边形有怎样的性质?
如果两个多边形相似,那么它们的对应角相等,对应边成比例.
作业布置
详见教材练习题
P8 第3,4,5题
谢
谢
第1章 图形的相似
九年级上册
1.1 相似多边形
课前小测
1.什么叫做全等三角形 它的形状、大小有何特征
能够安全重合的两个三角形叫全等三角形;
它们的形状相同,大小相等.
2.两个全等三角形的对应边和对应角有什么关系
对应边相等,对应角相等.
情境引入
问题:五星红旗是中华人民共和国的国旗,国旗上五颗星星形状相同吗?大小相等吗?
情境引入
形状相同,大小不相等.
情境引入
1.下列四组图形是相似形吗?
是
2.全等形与相似形有什么关系
全等形一定是相似形,相似形不一定是全等形.
是
是
是
情境引入
形状相同是对相似形的一种描述,你能利用两个相似多边形的各角之间及各边之间的数量关系表述它们形状相同的特征吗
合作探究
探究:相似多边形的概念和性质
小莹用电脑制作四边形ABCD,如图①,复制图①得到图②,把图①各边同时放大 得到图③;再把图①各边同时缩小 得到图④.
观察得到的四个四边形,你发现它们的形状和大小有什么特征 它们是相似形吗
形状相同,大小不同.它们是相似形.
合作探究
探究:相似多边形的概念和性质
合作探究
探究:相似多边形的概念和性质
(2)观察图①和图③,相应的角之间有怎样的数量关系 相应的各边的比之间有怎样的关系
,即对应边的比相等.
∠A= ∠ A‘’ ,∠ B= ∠ B ‘’,∠ C =∠ C‘’ ,∠ D =∠ D‘’,即对应角相等.
合作探究
探究:相似多边形的概念和性质
(3)观察图①和图④,相应的各角及相应的各边分别具有怎样的数量关系 图③和图④呢
③和④也是对应角相等,对应边的比值相等.
①和④对应角相等. ∠A= ∠ A''' ,∠ B= ∠ B ″′,∠ C =∠ C′′′,∠ D =∠ D'″
合作交流
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角相等,各边对应成比例,那么这两个多边形叫做相似多边形.
记法:四边形ABCD∽四边形A ′ B ′ C ′ D ′ .
读作:四边形ABCD“相似于”四边形A ′ B ′ C ′ D ′ .
相似比:相似多边形对应边的比叫做相似比.
相似多边形的性质:如果两个多边形相似,那么它们的对应角相等,对应边成比例.
定义:
合作探究
注意:
(1)对应顶点的字母写在对应的位置上.
(3)如果两个相似多边形相似比为1,那么这两个多边形全等.
(2)相似比是有顺序的.若正方形ABCD与正方形A1B1C1D1 的相似比为5:4,则正方A1B1C1D1与正方形ABCD的相似比为 .
4∶5
[例1]
下列说法正确的是( )
A.菱形都相似
B.正六边形都相似
C.矩形都相似
D.含80°角的等腰三角形都相似
B
典例分析
典例分析
解析:A.因为菱形的四条边相等,所以所有菱形的边对应成比例,但角不一定对应相等,所以菱 形不一定都相似,故本选项说法错误; B.因为正六边形的六条边相等,所以所有正六边形的边对应成比例,又因为正六边形的内 角都是120°,即角对应相等,所以正六边形都相似,故本选项说法正确;
C.因为矩形的内角都是90°,但边不一定对应成比例,所以矩形不一定都相似,故本选项中说法错误;
D.含80°角的等腰三角形,可能顶角是80°,也可能底角是80°,无法判定这样的等腰三角形相似,故本选项说法错误.
典例分析
[例2]
如图,四边形AEFD∽四边形EBCF.
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长.
解:(1)∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC,
(2)∵AD=3,EF=4且
,
,解得
.
.
∴
有两个多边形的各个角分别相等,能断定它们相似吗 由两个多边形的边对应成比例,能断定它们相似吗 如果不能,请分别举出反例;如果能,说明你的理由.
拓展
答:由两个多边形的各个角分别相等,不能断定他们相似,例如正方形和矩形,各个角分别相等但不相似.有两个多边形的边对应成比例,不能断定他们相似,例如正方形和菱形,各边对应成比例但不相似.
试一试
如图,已知△AOB∽△COD,∠A=∠C,则下列各式正确的有( )
A
B
O
C
D
A.1个 B.2个 C.3个 D.4个
A
归纳小结
1.相似多边形的定义
3.相似比
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角相等,各边对应成比例,那么这两个多边形叫做相似多边形.
2.相似多边形的性质
相似多边形对应边的比叫做相似比.
如果两个相似多边形相似比为1,那么这两个多边形全等.
如果两个多边形相似,那么它们的对应角相等,对应边成比例.
随堂检测
相似多边形课堂评价测试
同学们要认真答题哦!
随堂检测
1.下列四组图形中,不是相似形的是( )
B.
C.
D.
2.下列结论正确的有( )
(1)所有圆都相似;(2)所有正方形都相似;
(3)所有等腰三角形都相似;(4)所有矩形都相似.
A.1个 B.2个 C.3个 D.4个
3. 把一个长方形按如图所示的方式划分成三个全等的小长方形,每一个小长方形与原长方形相似,若小长方形的宽为2,则原长方形的宽x为______.
2
x
D
B
A.
随堂检测
4.两个相似多边形的相似比是3∶7,其中一个多边形的最长边是21, 则另一个多边形的最长边是________.
5.如图,菱形ABCD边长为3,∠B=60°,菱形A B C D 边长为5,∠C =120°,这两个菱形相似吗?试说明理由.
A
B
C
D
A'
B'
C'
D'
解:相似.理由如下:
∵四边形ABCD是菱形, ∠B=60 °,
∴∠A=120 °, ∠C=120 °, ∠D=60° .
∵四边形A B C D 是菱形,∠C =120° ,
∴∠A =120° , ∠B =60° , ∠D =60°,
∴∠A=∠A , ∠B= ∠B , ∠C= C , ∠D= ∠D ,
∴这两个菱形相似.
49或9
,
课堂小结
1.说一说相似形的定义;相似与全等的关系.
关系:全等形一定是相似形,相似形不一定是全等形.
2.相似多边形的概念、表示方法,相似比的定义是什么?
如果两个相似多边形的相似比为1,那么这两个多边形全等.
3.相似多边形有怎样的性质?
如果两个多边形相似,那么它们的对应角相等,对应边成比例.
作业布置
详见教材练习题
P8 第3,4,5题
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
