2.2 30°,45°,60°角的三角比 课件(共18张PPT)2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 2.2 30°,45°,60°角的三角比 课件(共18张PPT)2025-2026学年数学青岛版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第2章 解直角三角形
九年级上册
2.2 30°,45°,60°角的三角比
课前小测
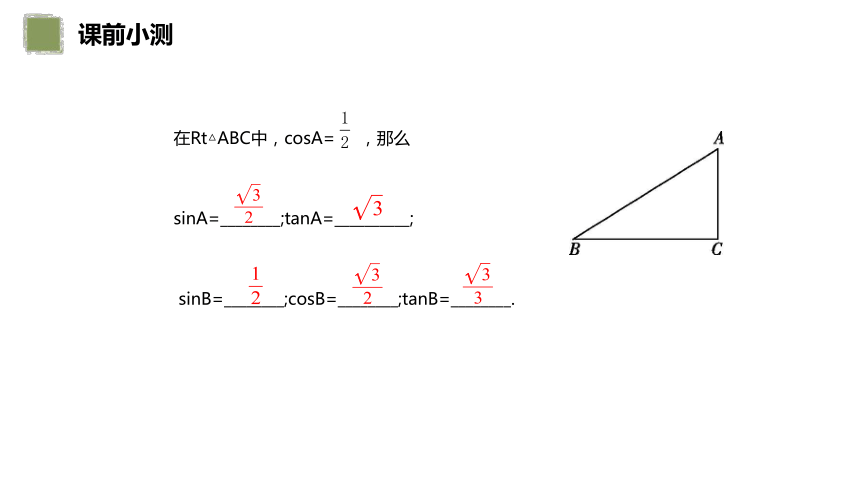
在Rt△ABC中,cosA= ,那么
sinA=________;tanA=__________;
sinB=________;cosB=________;tanB=________.
情境引入
同学们还记得如何用相似的知识去测量平时不能直接测量的物体的高度吗?
问题
情境引入
为了测量学校门前一棵大树的高度,可以用第1章所学的相似的知识设计方案求树高.但是,我这次准备了如下测量工具:①含45°或30°和60°角的三角尺;②皮尺.
设计方案如下:如图,当我们移动到的视线与树顶C和三角板的斜边在一条直线上时,量一下我们到树的距离BE(即得到AD的长)和眼睛到地面的距离AB,就可以求树高.根据上述条件你能否直接求出大树的高度
情境引入
你能求出45°或30°或60°角的三个三角比的值吗?
合作探究
探究一:45°角的三角比的值
观察一副三角尺,其中有几个锐角 它们分别等于多少度
都是两个锐角,分别是45°,45 °和30 °, 60 °.
合作探究
探究一: 45°角的三角比的值
1.sin45 ,cos45 ,tan45 的值分别是什么?
A
B
C
作Rt△ ABC,使∠ C = 90°, ∠ A = 45°(如图).
设 a = 1,那么 b = 1.由勾股定理得,
合作探究
探究二:30°角的三角比的值
sin30 °,cos30 °,tan30 °的值分别是多少?
分析:取两个含30 的角的大小相等的三角尺,按下图的方式拼在一起,
得到的△ABC是怎样的三角形?为什么?
因为∠ A =∠ B = 60°,所以△ ABC 是等边三角形,且 CD是 AB 边上的高, AD = BD .
在 Rt△ ADC 中, ∠ ADC = 90°, ∠ ACD = 30°.设 AC = 1,那么
合作探究
探究三: 60°角的三角比的值
你会求出60 角的正弦,余弦和正切的值吗?与同学交流.
归纳小结
把30 ,45 ,60 角的正弦,余弦和正切的值填入下表:
角α 三角比 30 45 60
sinα
cosα
tanα
从填写的表格中,你发现了哪些规律?与同学交流.
(1)如果∠A+∠B=90 ,那么sinA=cosB,tanA·tanB=1.利用这个规律便于记忆.
1
(2)正弦,正切的值随着角的度数的增大而增大.余弦值随着度数的增大而减小.
典例分析
[例1]
求下列各式的值。
(1)sin30 ·cos45 ;
(2)tan45 -cos60 .
[例2]
典例分析
在Rt△ABC中 ,已知sinA=
,求锐角A的度数.
归纳小结:当A,B都是锐角时,如果sinA=sinB或cosA=cosB或tanA=tanB, 那么A=B.利用这个结论,知道一个锐角的三角比,可以反过来求这个锐角.
拓展
sin15 和sin75 的值是多少呢?你是怎样得到的?
随堂检测
30 °, 45°,60 °角的三角比
课堂评价测试
同学们要认真答题哦!
随堂检测
D
课堂小结
熟记30 ,45 ,60 的三角比的值.
如果∠A+∠B=90 ,那么sinA=cosB,tanA·tanB=1.
如果sinA=sinB或cosA=cosB或tanA=tanB,那么A=B.利用这个结论,知道一个锐角的三角比,可以反过来求这个锐角.
作业布置
详见教材练习题
P44 T1-2
谢
谢
第2章 解直角三角形
九年级上册
2.2 30°,45°,60°角的三角比
课前小测
在Rt△ABC中,cosA= ,那么
sinA=________;tanA=__________;
sinB=________;cosB=________;tanB=________.
情境引入
同学们还记得如何用相似的知识去测量平时不能直接测量的物体的高度吗?
问题
情境引入
为了测量学校门前一棵大树的高度,可以用第1章所学的相似的知识设计方案求树高.但是,我这次准备了如下测量工具:①含45°或30°和60°角的三角尺;②皮尺.
设计方案如下:如图,当我们移动到的视线与树顶C和三角板的斜边在一条直线上时,量一下我们到树的距离BE(即得到AD的长)和眼睛到地面的距离AB,就可以求树高.根据上述条件你能否直接求出大树的高度
情境引入
你能求出45°或30°或60°角的三个三角比的值吗?
合作探究
探究一:45°角的三角比的值
观察一副三角尺,其中有几个锐角 它们分别等于多少度
都是两个锐角,分别是45°,45 °和30 °, 60 °.
合作探究
探究一: 45°角的三角比的值
1.sin45 ,cos45 ,tan45 的值分别是什么?
A
B
C
作Rt△ ABC,使∠ C = 90°, ∠ A = 45°(如图).
设 a = 1,那么 b = 1.由勾股定理得,
合作探究
探究二:30°角的三角比的值
sin30 °,cos30 °,tan30 °的值分别是多少?
分析:取两个含30 的角的大小相等的三角尺,按下图的方式拼在一起,
得到的△ABC是怎样的三角形?为什么?
因为∠ A =∠ B = 60°,所以△ ABC 是等边三角形,且 CD是 AB 边上的高, AD = BD .
在 Rt△ ADC 中, ∠ ADC = 90°, ∠ ACD = 30°.设 AC = 1,那么
合作探究
探究三: 60°角的三角比的值
你会求出60 角的正弦,余弦和正切的值吗?与同学交流.
归纳小结
把30 ,45 ,60 角的正弦,余弦和正切的值填入下表:
角α 三角比 30 45 60
sinα
cosα
tanα
从填写的表格中,你发现了哪些规律?与同学交流.
(1)如果∠A+∠B=90 ,那么sinA=cosB,tanA·tanB=1.利用这个规律便于记忆.
1
(2)正弦,正切的值随着角的度数的增大而增大.余弦值随着度数的增大而减小.
典例分析
[例1]
求下列各式的值。
(1)sin30 ·cos45 ;
(2)tan45 -cos60 .
[例2]
典例分析
在Rt△ABC中 ,已知sinA=
,求锐角A的度数.
归纳小结:当A,B都是锐角时,如果sinA=sinB或cosA=cosB或tanA=tanB, 那么A=B.利用这个结论,知道一个锐角的三角比,可以反过来求这个锐角.
拓展
sin15 和sin75 的值是多少呢?你是怎样得到的?
随堂检测
30 °, 45°,60 °角的三角比
课堂评价测试
同学们要认真答题哦!
随堂检测
D
课堂小结
熟记30 ,45 ,60 的三角比的值.
如果∠A+∠B=90 ,那么sinA=cosB,tanA·tanB=1.
如果sinA=sinB或cosA=cosB或tanA=tanB,那么A=B.利用这个结论,知道一个锐角的三角比,可以反过来求这个锐角.
作业布置
详见教材练习题
P44 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
