2.3 用计算器求锐角三角比 课件(共21张PPT)2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 2.3 用计算器求锐角三角比 课件(共21张PPT)2025-2026学年数学青岛版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:33:45 | ||
图片预览








文档简介
(共21张PPT)
第2章 解直角三角形
九年级上册
2.3 用计算器求锐角三角比
课前小测
A
75°
解:|-3|+2cos 45°-( -1)0
=3+2× -1
=3+ -1
=2+ .
.
情境引入
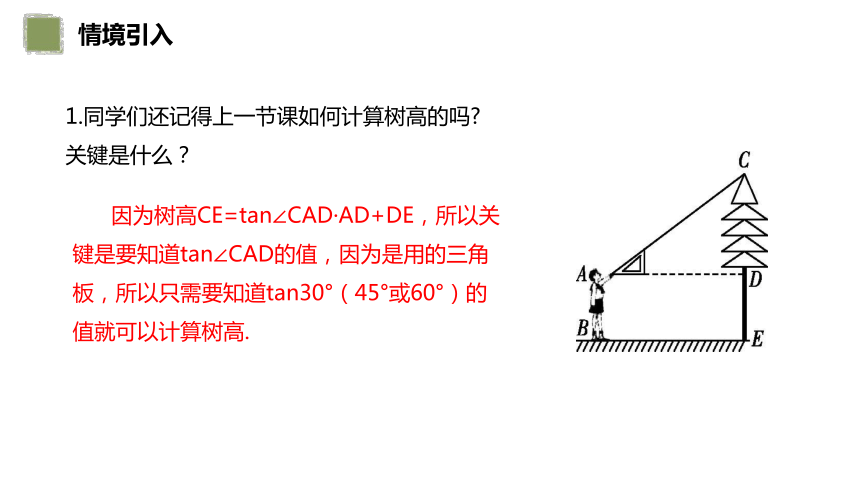
问题:同学们还记得上一节课如何计算树高的吗 关键是什么?
情境引入
1.同学们还记得上一节课如何计算树高的吗 关键是什么?
因为树高CE=tan∠CAD·AD+DE,所以关键是要知道tan∠CAD的值,因为是用的三角板,所以只需要知道tan30°(45°或60°)的值就可以计算树高.
情境引入
2.但是这样局限性很强,必须是特殊角才能求树高,有没有更一般的方法呢?
有,但是需要一个工具,那就是计算器.
咱们本节课学习如何用计算器来求三角比的值.
用计算器可以求出任意角度的三角比的值.
合作探究
探究一:用计算器求三角比的值
问题1: 把计算器设置成什么状态才能求三角比的值呢?
首先要进入以“度”为角的度量单位的运算状态. 即启动开机键后,使显示器的上方显示 DEG(如果没有显示 DEG,可以按 DR 1 键).
因计算器的种类不同,键盘上各键的功能符号和按键顺序可能不同. 使用计算器前,应先阅读使用说明书,以免使用中出现计算错误.
合作探究
探究一:用计算器求三角比的值
问题2:已知角的度数求三角比的值按照什么顺序输入呢?
在“度”为角的度量单位的运算状态下,先按sin,cos,或tan键再输入锐角的度数,按=键后,显示器上显示的数字就是三角比的值.
若角度单位是度、分、秒时,要按DMS 键.
典例分析
[例1]
用计算器求下列锐角三角比的值(精确到 0.000 1):
(1) sin 47°; (2) cos 56.3°;(3) tan 35° 10' 22'' .
解:在角的度量单位为“度”的状态下(显示器上方显示 DEG).
(1)按下列顺序依次按键:sin 47 DMS = ,屏幕上显示 0.731 353 701,按精确到 0.000 1 取近似值,得 sin47° ≈ 0.731 4;
(2)按下列顺序依次按键:cos 56 · 3 DMS = ,屏幕上显示0.554 844 427,按精确到0.000 1取近似值,得cos56.3° ≈ 0.554 8;
(3)按下列顺序依次按键:tan 35 DMS 10 DMS 22 DMS = ,屏幕上显示0.704 711 093,按精确到0.000 1取近似值,得tan35° 10'22'' ≈ 0.704 7.
[例2]
典例分析
用计算器求下列锐角三角比的值(精确到 0.000 1):
(1)
(2) sin 9‘.
解:在角的度量单位为“度”的状态下,
(1)按下列顺序依次按键:
tan ( 80 ÷ 3 ) DMS = ,屏幕上显示0.502 218 876,按精确到0.000 1取近似值,得
≈0.502 2;
(2)按下列顺序依次按键:
sin 0 DMS 9 DMS = ,屏幕上显示2.617 990 887× 10-3,按精确到0.000 1取近似值,得sin9' ≈ 0.002 6.
归纳小结
已知角的度数求三角比的值时,
(1)要在DEG状态下输入;
(2)按键顺序要正确,输入度、分、秒时要按DMS键,当缺少度或分或秒时要用“0”来补全.
合作探究
探究二:用计算器求角的度数
计算器在什么状态下,以怎样的顺序输入才能求角的度数呢?
在角的度量单位为“度”的状态下,先按副功能键 2ndF和相应三角比的名称键,再输入三角比的值,按 = 键后,屏幕上就可以显示以度为单位的锐角.
典例分析
根据下列三角比的值,用计算器求相应的锐角 A(精确到 1''):
(1) sin A = 0.618 5; (2) tan A = 3.207 8.
[例3]
解:在角的度量单位为“度”的状态下,
(1)按下列顺序依次按键:
2ndF sin 0 · 6185 = ,屏幕上显示 38.206 679 08°,即锐角 A ≈ 38.206 679 08°.再按 DMS 键,将它换算成“度、分、秒”的形式,屏幕上显示 38° 12' 24.04'' ,
所以锐角 A ≈ 38° 12' 24'' ;
(2)按下列顺序依次按键:
2ndF tan 3 · 2078 = ,屏幕上显示 72.685 647 68°,即锐角 A ≈ 72.685 647 68°.再按 DMS 键,将它换算成“度、分、秒”的形式,屏幕上显示 72° 41' 8.33'',所以锐角 A ≈ 72° 41' 8'' .
典例分析
[例4]
利用计算器求下列各式的值:
(1)sin 20°· tan 35°;(2)
解:在角的度量单位为“度”的状态下,
(1)按下列顺序依次按键:sin 20 DMS × tan 35 DMS = ,屏幕上显示 0.239 485 082,所以 sin 20°· tan 35° ≈ 0.239 5;
≈ 0.748 9.
(2)按下列顺序依次按键:
1 ab/c 2 × sin 30 DMS 26 DMS+
2 ÷ 2 × cos 45 DMS 30 DMS 8 DMS=,
屏幕上显示 0.748 865 866,所以
.
归纳小结
已知三角比求对应角的度数和已知度数求三角比,在用计算器操作时是不同的,不要混淆.
例3中,求出度数后精确到秒,一定再按DMS键才能化为度分秒.
例4是利用计算器进行锐角三角比的简单运算,一定要注意按键的顺序,并把结果四舍五入到千分位.
拓展
利用计算器求下列锐角三角比的值,填写下表:
角α 三角比 1° 10° 20° 30° 40° 45° 50° 60° 70° 80° 89°
Sinα
cosα
0.017 5
0.173 6
0.342 0
0.5
0.642 8
0.707 1
0.766 0
0.866 0
0.984 8
0.939 7
0.999 8
0.999 8
0.984 8
0.939 7
0.866 0
0.766 0
0.707 1
0.642 8
0.5
0.342 0
0.173 6
0.017 5
观察上表,并回答下列问题:
(1)当锐角α 逐渐增大时,它的正弦和余弦的值分别发生怎样的变化?
当角度逐渐增大时,正弦值也逐渐增大,余弦值逐渐减小.
(2)你能估计出锐角α 的正弦值的范围吗?锐角α 的余弦值的范围呢?
0(3)你还能从表中发现什么规律?
一个锐角的正(余)弦值,等于它的余角的余(正)弦值.
随堂检测
用计算器求锐角三角比
课堂评价测试
同学们要认真答题哦!
随堂检测
解:sin 13.6°≈0.2351,sin 56° 12' 10''≈0.8310,sin 50' 23''≈0.0147.
解:(1)40°35′39.84″.(2)74°34′46.42″.(3)20°19′46.8″.
解: = -0.0580.
随堂检测
4. 用计算器分别求出下列三组三角比的值:
(1)sin 13°, cos 77°;
(2) sin 62° 18‘, cos 27° 42’;
(3) sin 83° 21', cos 6° 39' .
由此你发现了什么规律?
解:(1)sin 13°≈0.2250, cos 77°≈0.2250;
(2) sin 62° 18'≈0.8854, cos 27° 42'≈0.8854;
(3)sin 83° 21'≈0.9933, cos 6° 39'≈0.9933.
规律:若A+B=90°,则sinA=cosB .
课堂小结
1.用计算器求三角比的值需要注意什么?
要在DEG状态下输入;
按键顺序要正确,输入度、分、秒时要按DMS键,当缺少度或分或秒时要用“0”来补全.
2.用计算器求角的度数需要注意什么?
求出度数后精确到秒,一定再按DMS键才能化为度分秒.
利用计算器进行锐角三角比的简单运算,一定要注意按键的顺序,并把结果四舍五入到千分位.
3.锐角的正弦、余弦随着角度的变化有怎样的变化规律
当角度逐渐增大时,正弦值也逐渐增大,余弦值逐渐减小.
作业布置
详见教材练习题
P47 T1-2
P48 T1-2
谢
谢
第2章 解直角三角形
九年级上册
2.3 用计算器求锐角三角比
课前小测
A
75°
解:|-3|+2cos 45°-( -1)0
=3+2× -1
=3+ -1
=2+ .
.
情境引入
问题:同学们还记得上一节课如何计算树高的吗 关键是什么?
情境引入
1.同学们还记得上一节课如何计算树高的吗 关键是什么?
因为树高CE=tan∠CAD·AD+DE,所以关键是要知道tan∠CAD的值,因为是用的三角板,所以只需要知道tan30°(45°或60°)的值就可以计算树高.
情境引入
2.但是这样局限性很强,必须是特殊角才能求树高,有没有更一般的方法呢?
有,但是需要一个工具,那就是计算器.
咱们本节课学习如何用计算器来求三角比的值.
用计算器可以求出任意角度的三角比的值.
合作探究
探究一:用计算器求三角比的值
问题1: 把计算器设置成什么状态才能求三角比的值呢?
首先要进入以“度”为角的度量单位的运算状态. 即启动开机键后,使显示器的上方显示 DEG(如果没有显示 DEG,可以按 DR 1 键).
因计算器的种类不同,键盘上各键的功能符号和按键顺序可能不同. 使用计算器前,应先阅读使用说明书,以免使用中出现计算错误.
合作探究
探究一:用计算器求三角比的值
问题2:已知角的度数求三角比的值按照什么顺序输入呢?
在“度”为角的度量单位的运算状态下,先按sin,cos,或tan键再输入锐角的度数,按=键后,显示器上显示的数字就是三角比的值.
若角度单位是度、分、秒时,要按DMS 键.
典例分析
[例1]
用计算器求下列锐角三角比的值(精确到 0.000 1):
(1) sin 47°; (2) cos 56.3°;(3) tan 35° 10' 22'' .
解:在角的度量单位为“度”的状态下(显示器上方显示 DEG).
(1)按下列顺序依次按键:sin 47 DMS = ,屏幕上显示 0.731 353 701,按精确到 0.000 1 取近似值,得 sin47° ≈ 0.731 4;
(2)按下列顺序依次按键:cos 56 · 3 DMS = ,屏幕上显示0.554 844 427,按精确到0.000 1取近似值,得cos56.3° ≈ 0.554 8;
(3)按下列顺序依次按键:tan 35 DMS 10 DMS 22 DMS = ,屏幕上显示0.704 711 093,按精确到0.000 1取近似值,得tan35° 10'22'' ≈ 0.704 7.
[例2]
典例分析
用计算器求下列锐角三角比的值(精确到 0.000 1):
(1)
(2) sin 9‘.
解:在角的度量单位为“度”的状态下,
(1)按下列顺序依次按键:
tan ( 80 ÷ 3 ) DMS = ,屏幕上显示0.502 218 876,按精确到0.000 1取近似值,得
≈0.502 2;
(2)按下列顺序依次按键:
sin 0 DMS 9 DMS = ,屏幕上显示2.617 990 887× 10-3,按精确到0.000 1取近似值,得sin9' ≈ 0.002 6.
归纳小结
已知角的度数求三角比的值时,
(1)要在DEG状态下输入;
(2)按键顺序要正确,输入度、分、秒时要按DMS键,当缺少度或分或秒时要用“0”来补全.
合作探究
探究二:用计算器求角的度数
计算器在什么状态下,以怎样的顺序输入才能求角的度数呢?
在角的度量单位为“度”的状态下,先按副功能键 2ndF和相应三角比的名称键,再输入三角比的值,按 = 键后,屏幕上就可以显示以度为单位的锐角.
典例分析
根据下列三角比的值,用计算器求相应的锐角 A(精确到 1''):
(1) sin A = 0.618 5; (2) tan A = 3.207 8.
[例3]
解:在角的度量单位为“度”的状态下,
(1)按下列顺序依次按键:
2ndF sin 0 · 6185 = ,屏幕上显示 38.206 679 08°,即锐角 A ≈ 38.206 679 08°.再按 DMS 键,将它换算成“度、分、秒”的形式,屏幕上显示 38° 12' 24.04'' ,
所以锐角 A ≈ 38° 12' 24'' ;
(2)按下列顺序依次按键:
2ndF tan 3 · 2078 = ,屏幕上显示 72.685 647 68°,即锐角 A ≈ 72.685 647 68°.再按 DMS 键,将它换算成“度、分、秒”的形式,屏幕上显示 72° 41' 8.33'',所以锐角 A ≈ 72° 41' 8'' .
典例分析
[例4]
利用计算器求下列各式的值:
(1)sin 20°· tan 35°;(2)
解:在角的度量单位为“度”的状态下,
(1)按下列顺序依次按键:sin 20 DMS × tan 35 DMS = ,屏幕上显示 0.239 485 082,所以 sin 20°· tan 35° ≈ 0.239 5;
≈ 0.748 9.
(2)按下列顺序依次按键:
1 ab/c 2 × sin 30 DMS 26 DMS+
2 ÷ 2 × cos 45 DMS 30 DMS 8 DMS=,
屏幕上显示 0.748 865 866,所以
.
归纳小结
已知三角比求对应角的度数和已知度数求三角比,在用计算器操作时是不同的,不要混淆.
例3中,求出度数后精确到秒,一定再按DMS键才能化为度分秒.
例4是利用计算器进行锐角三角比的简单运算,一定要注意按键的顺序,并把结果四舍五入到千分位.
拓展
利用计算器求下列锐角三角比的值,填写下表:
角α 三角比 1° 10° 20° 30° 40° 45° 50° 60° 70° 80° 89°
Sinα
cosα
0.017 5
0.173 6
0.342 0
0.5
0.642 8
0.707 1
0.766 0
0.866 0
0.984 8
0.939 7
0.999 8
0.999 8
0.984 8
0.939 7
0.866 0
0.766 0
0.707 1
0.642 8
0.5
0.342 0
0.173 6
0.017 5
观察上表,并回答下列问题:
(1)当锐角α 逐渐增大时,它的正弦和余弦的值分别发生怎样的变化?
当角度逐渐增大时,正弦值也逐渐增大,余弦值逐渐减小.
(2)你能估计出锐角α 的正弦值的范围吗?锐角α 的余弦值的范围呢?
0
一个锐角的正(余)弦值,等于它的余角的余(正)弦值.
随堂检测
用计算器求锐角三角比
课堂评价测试
同学们要认真答题哦!
随堂检测
解:sin 13.6°≈0.2351,sin 56° 12' 10''≈0.8310,sin 50' 23''≈0.0147.
解:(1)40°35′39.84″.(2)74°34′46.42″.(3)20°19′46.8″.
解: = -0.0580.
随堂检测
4. 用计算器分别求出下列三组三角比的值:
(1)sin 13°, cos 77°;
(2) sin 62° 18‘, cos 27° 42’;
(3) sin 83° 21', cos 6° 39' .
由此你发现了什么规律?
解:(1)sin 13°≈0.2250, cos 77°≈0.2250;
(2) sin 62° 18'≈0.8854, cos 27° 42'≈0.8854;
(3)sin 83° 21'≈0.9933, cos 6° 39'≈0.9933.
规律:若A+B=90°,则sinA=cosB .
课堂小结
1.用计算器求三角比的值需要注意什么?
要在DEG状态下输入;
按键顺序要正确,输入度、分、秒时要按DMS键,当缺少度或分或秒时要用“0”来补全.
2.用计算器求角的度数需要注意什么?
求出度数后精确到秒,一定再按DMS键才能化为度分秒.
利用计算器进行锐角三角比的简单运算,一定要注意按键的顺序,并把结果四舍五入到千分位.
3.锐角的正弦、余弦随着角度的变化有怎样的变化规律
当角度逐渐增大时,正弦值也逐渐增大,余弦值逐渐减小.
作业布置
详见教材练习题
P47 T1-2
P48 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
