3.1 圆的对称性 第1课时 垂径定理 课件 2025-2026学年数学青岛版九年级上册(共22张PPT)
文档属性
| 名称 | 3.1 圆的对称性 第1课时 垂径定理 课件 2025-2026学年数学青岛版九年级上册(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第3章 对圆的进一步认识
九年级上册
3.1 圆的对称性
第1课时 垂径定理
课前小测
1.圆是平面内到__________距离等于________的点的集合.
2.弦:圆上任意两点之间所连接的线段叫作_______,圆中最长的弦是______.
3.弧:圆上任意两点间的部分叫作______,简称弧.用符号“______”表示.
半圆:一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.
弧的分类 优弧:___________________叫做优弧.
劣弧:___________________叫做劣弧.
B
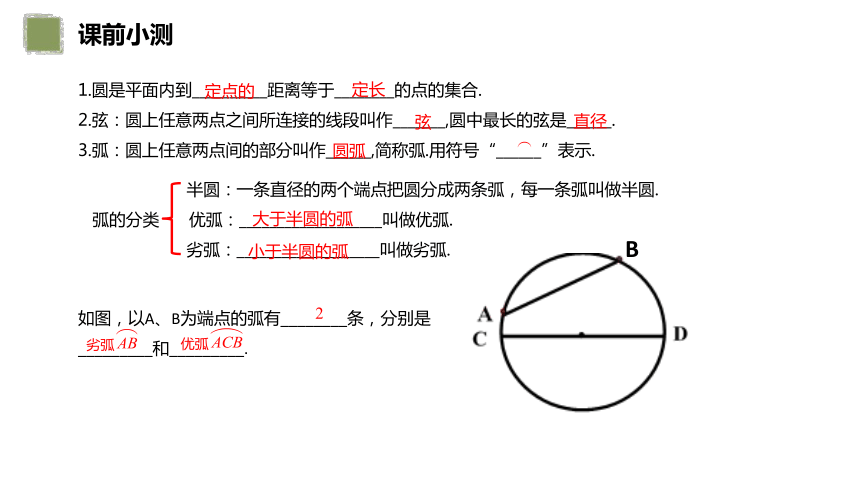
如图,以A、B为端点的弧有________条,分别是_________和_________.
定点的
定长
弦
直径
圆弧
大于半圆的弧
小于半圆的弧
2
情境引入
问题:同学们知道北京天坛公园的圜丘坛吗?
情境引入
这是北京天坛公园内圜丘坛的照片.
圜丘坛,俗称祭天台,高5米,直径23米,是一座由白玉石雕栏围绕的三层石造圆台.
观察这幅图片,思考下面的问题:
圆是轴对称图形吗?是中心对称图形吗?
是轴对称图形,也是中心对称图形.
2. 如果站在圜丘坛最上一层,你能准确找到它的圆心吗?
怎么能准确找到圆心呢,等学完这一章,同学们就会有各种办法.
情境引入
圆是轴对称图形吗?
你能找到它的对称轴吗?
合作探究
探究一:圆是轴对称图形吗?
思考下面的问题,动手操作并与同学交流:
(1)在一张半透明的纸片上画一个圆,标出它的圆心O,再任意作出一条直径 AB.将⊙O沿直径AB折叠,你发现了什么?
折叠后两边完全重合.
(2)再任意作一条直径,重复(1)中的操作,还有同样的结论吗?
折叠后还是两边完全重合.
归纳总结:
圆是轴对称图形,每一条直径所在的直线都是它的对称轴.
合作探究
探究二:垂径定理和推论
如图,CD是⊙O的弦,AB是与CD垂直的直径,垂足为点E . 将⊙O沿直径AB折叠.
1.垂径定理
合作探究
探究二:垂径定理和推论
(2)能不能通过推理得到结论呢?
证明:连接OC,OD.∵OC = OD, OE⊥CD, OE = OE,
∴ Rt△OCE≌Rt△ODE,∴ CE = DE .
∴点C与点D关于直线 AB 对称.
∵直线 AB 是⊙O 的对称轴,
∴当⊙O沿直线AB折叠时,点C与点D重合,
与
重合,
与
重合,
∴
归纳小结
垂径定理 垂直于弦的直径平分弦以及弦所对的两条弧.
归纳小结
“垂直于弦的直径”可以是直径,也可以是半径(如图),甚至还可以是过圆心的直线或线段.
合作探究
探究二:垂径定理和推论
由折叠或如垂径定理的证明可知,下列推论成立.
推论1:
平分弦(不是直径)的直径,垂直这条弦,并且平分这条弦所对的两条弧.
C
D
如图,两条直径一定互相平分,但不一定垂直,所以被平分的弦如果是直径,结论不一定成立.
2.垂径定理的推论
合作探究
推论2:
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
推论3:
平分弦所对的一条弧的直径,垂直平分这条弦,并且平分这条弦所对的另一条弧.
归纳小结
一条线,①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧,知二推三.
典例分析
[例1]
如图,以△OAB 的顶点O为圆心的⊙O 交AB 于点C,D,且AC
= BD . 求证:OA = OB .
E
证明:作 OE⊥ AB,垂足为点 E.
由垂径定理,得 CE = DE .
∵ AC = BD,
∴ AC + CE = BD + DE,即 AE = BE .
∴ OE 为线段 AB 的垂直平分线.
∴ OA = OB .
圆心到弦的垂线段的长度称为这条弦的弦心距.例如:OE是CD的弦心距.
归纳总结:在圆中,作弦心距是常用的辅助线,可以利用垂径定理产生的结论来推理.
[例2]
典例分析
1400多年前,我国隋朝时期建造的赵州石拱桥(如图)的桥拱近似于圆弧形,它的跨度(弧所对的弦长)为37.02 m,拱高(弧的中点到弦的距离,也叫弓形的高)为 7.23 m .求桥拱所在圆的半径(精确到 0.1 m).
归纳小结
作弦心距和连半径是圆中常见的辅助线,应用垂径定理构造直角三角形,结合勾股定理来解决的.
a
拓展:
设半径OC=r,弦心距OE=d,弦CD的一半CE(半弦)为a,拱高AE为m,在这四个量r,d,a,m中,知二推二.
随堂检测
垂径定理 课堂评价测试
同学们要认真答题哦!
随堂检测
C
B
随堂检测
3.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知AB=16,CM=4,求OA.
└
课堂小结
圆具有怎样的对称性?
垂径定理及其推论的内容是什么?
一条线,①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧,知二推三.
在圆中,经常作弦心距、连半径、和半弦构造直角三角形,利用勾股定理求线段长度.弦心距、半径、半弦、拱高知二推二.
3.在圆中,通常怎样构造直角三角形解决问题
作业布置
详见教材练习题
P70 T1-2
谢
谢
第3章 对圆的进一步认识
九年级上册
3.1 圆的对称性
第1课时 垂径定理
课前小测
1.圆是平面内到__________距离等于________的点的集合.
2.弦:圆上任意两点之间所连接的线段叫作_______,圆中最长的弦是______.
3.弧:圆上任意两点间的部分叫作______,简称弧.用符号“______”表示.
半圆:一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.
弧的分类 优弧:___________________叫做优弧.
劣弧:___________________叫做劣弧.
B
如图,以A、B为端点的弧有________条,分别是_________和_________.
定点的
定长
弦
直径
圆弧
大于半圆的弧
小于半圆的弧
2
情境引入
问题:同学们知道北京天坛公园的圜丘坛吗?
情境引入
这是北京天坛公园内圜丘坛的照片.
圜丘坛,俗称祭天台,高5米,直径23米,是一座由白玉石雕栏围绕的三层石造圆台.
观察这幅图片,思考下面的问题:
圆是轴对称图形吗?是中心对称图形吗?
是轴对称图形,也是中心对称图形.
2. 如果站在圜丘坛最上一层,你能准确找到它的圆心吗?
怎么能准确找到圆心呢,等学完这一章,同学们就会有各种办法.
情境引入
圆是轴对称图形吗?
你能找到它的对称轴吗?
合作探究
探究一:圆是轴对称图形吗?
思考下面的问题,动手操作并与同学交流:
(1)在一张半透明的纸片上画一个圆,标出它的圆心O,再任意作出一条直径 AB.将⊙O沿直径AB折叠,你发现了什么?
折叠后两边完全重合.
(2)再任意作一条直径,重复(1)中的操作,还有同样的结论吗?
折叠后还是两边完全重合.
归纳总结:
圆是轴对称图形,每一条直径所在的直线都是它的对称轴.
合作探究
探究二:垂径定理和推论
如图,CD是⊙O的弦,AB是与CD垂直的直径,垂足为点E . 将⊙O沿直径AB折叠.
1.垂径定理
合作探究
探究二:垂径定理和推论
(2)能不能通过推理得到结论呢?
证明:连接OC,OD.∵OC = OD, OE⊥CD, OE = OE,
∴ Rt△OCE≌Rt△ODE,∴ CE = DE .
∴点C与点D关于直线 AB 对称.
∵直线 AB 是⊙O 的对称轴,
∴当⊙O沿直线AB折叠时,点C与点D重合,
与
重合,
与
重合,
∴
归纳小结
垂径定理 垂直于弦的直径平分弦以及弦所对的两条弧.
归纳小结
“垂直于弦的直径”可以是直径,也可以是半径(如图),甚至还可以是过圆心的直线或线段.
合作探究
探究二:垂径定理和推论
由折叠或如垂径定理的证明可知,下列推论成立.
推论1:
平分弦(不是直径)的直径,垂直这条弦,并且平分这条弦所对的两条弧.
C
D
如图,两条直径一定互相平分,但不一定垂直,所以被平分的弦如果是直径,结论不一定成立.
2.垂径定理的推论
合作探究
推论2:
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
推论3:
平分弦所对的一条弧的直径,垂直平分这条弦,并且平分这条弦所对的另一条弧.
归纳小结
一条线,①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧,知二推三.
典例分析
[例1]
如图,以△OAB 的顶点O为圆心的⊙O 交AB 于点C,D,且AC
= BD . 求证:OA = OB .
E
证明:作 OE⊥ AB,垂足为点 E.
由垂径定理,得 CE = DE .
∵ AC = BD,
∴ AC + CE = BD + DE,即 AE = BE .
∴ OE 为线段 AB 的垂直平分线.
∴ OA = OB .
圆心到弦的垂线段的长度称为这条弦的弦心距.例如:OE是CD的弦心距.
归纳总结:在圆中,作弦心距是常用的辅助线,可以利用垂径定理产生的结论来推理.
[例2]
典例分析
1400多年前,我国隋朝时期建造的赵州石拱桥(如图)的桥拱近似于圆弧形,它的跨度(弧所对的弦长)为37.02 m,拱高(弧的中点到弦的距离,也叫弓形的高)为 7.23 m .求桥拱所在圆的半径(精确到 0.1 m).
归纳小结
作弦心距和连半径是圆中常见的辅助线,应用垂径定理构造直角三角形,结合勾股定理来解决的.
a
拓展:
设半径OC=r,弦心距OE=d,弦CD的一半CE(半弦)为a,拱高AE为m,在这四个量r,d,a,m中,知二推二.
随堂检测
垂径定理 课堂评价测试
同学们要认真答题哦!
随堂检测
C
B
随堂检测
3.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知AB=16,CM=4,求OA.
└
课堂小结
圆具有怎样的对称性?
垂径定理及其推论的内容是什么?
一条线,①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧,知二推三.
在圆中,经常作弦心距、连半径、和半弦构造直角三角形,利用勾股定理求线段长度.弦心距、半径、半弦、拱高知二推二.
3.在圆中,通常怎样构造直角三角形解决问题
作业布置
详见教材练习题
P70 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
