3.3第1课时 圆周角定理及推论1 课件(共21张PPT) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 3.3第1课时 圆周角定理及推论1 课件(共21张PPT) 2025-2026学年数学青岛版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:48:14 | ||
图片预览




文档简介
(共21张PPT)
第3章 对圆的进一步认识
九年级上册
3.3 圆周角
第1课时 圆周角定理及推论1
课前小测
1.圆心角的定义
2.圆心角的度数和它所对的弧的度数的关系
顶点在圆心的角叫作圆心角.
圆心角的度数与它所对的弧的度数相等
情境引入
问题:你知道什么是圆周角吗?
情境引入
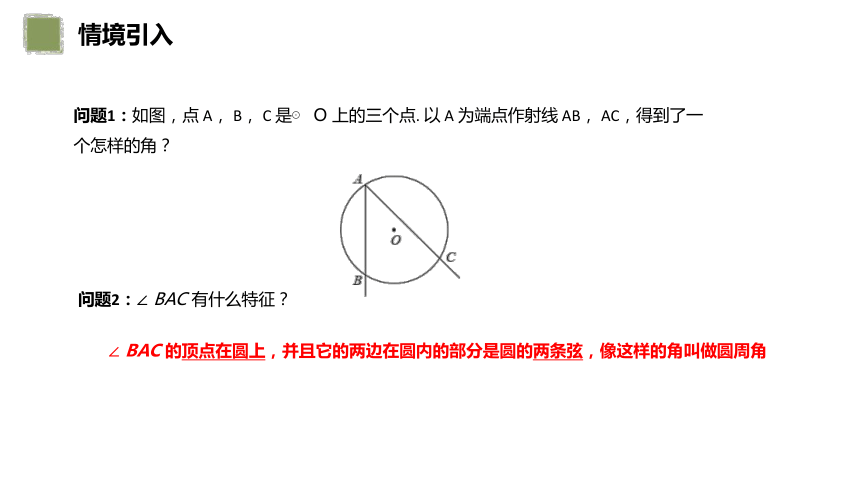
问题1:如图,点 A, B, C 是⊙ O 上的三个点. 以 A 为端点作射线 AB, AC,得到了一个怎样的角?
问题2:∠ BAC 有什么特征?
∠ BAC 的顶点在圆上,并且它的两边在圆内的部分是圆的两条弦,像这样的角叫做圆周角
情境引入
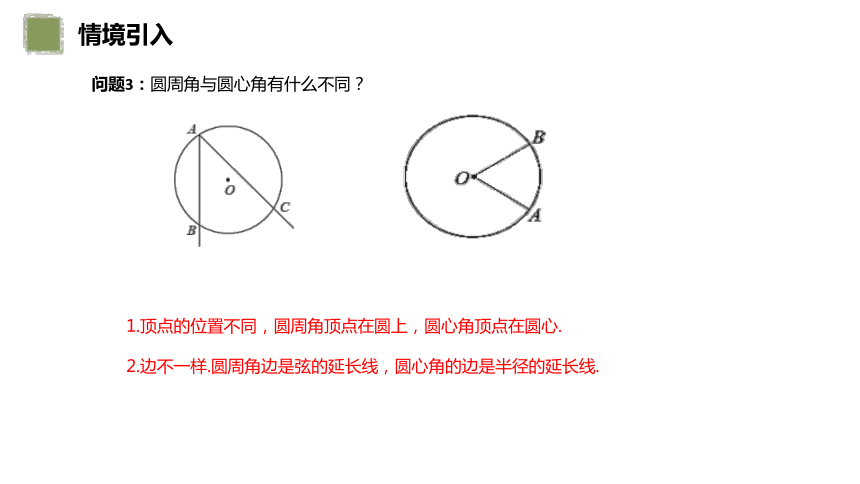
问题3:圆周角与圆心角有什么不同?
1.顶点的位置不同,圆周角顶点在圆上,圆心角顶点在圆心.
2.边不一样.圆周角边是弦的延长线,圆心角的边是半径的延长线.
情境引入
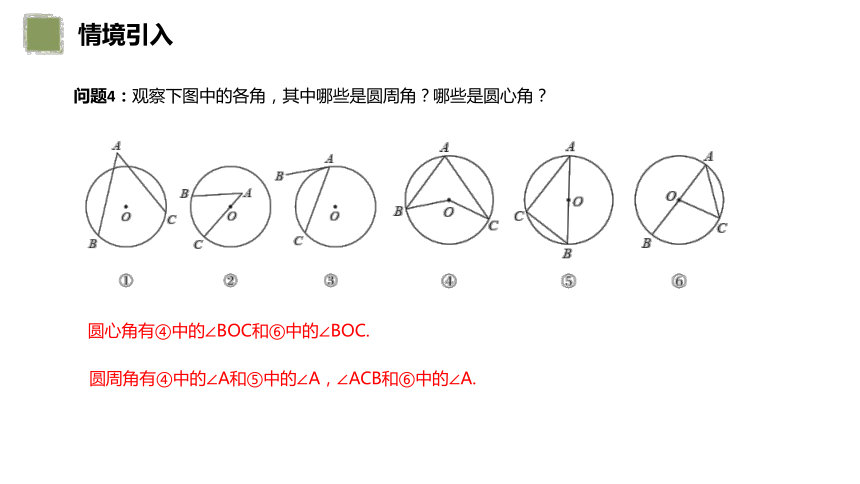
问题4:观察下图中的各角,其中哪些是圆周角?哪些是圆心角?
圆心角有④中的∠BOC和⑥中的∠BOC.
圆周角有④中的∠A和⑤中的∠A,∠ACB和⑥中的∠A.
情境引入
你知道圆周角有哪些性质吗?
合作探究
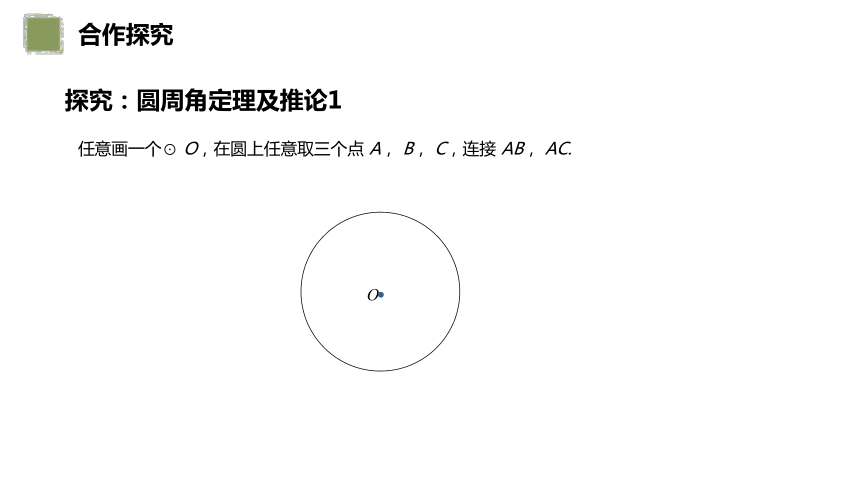
探究:圆周角定理及推论1
任意画一个⊙ O,在圆上任意取三个点 A, B, C,连接 AB, AC.
O
合作探究
探究:圆周角定理及推论1
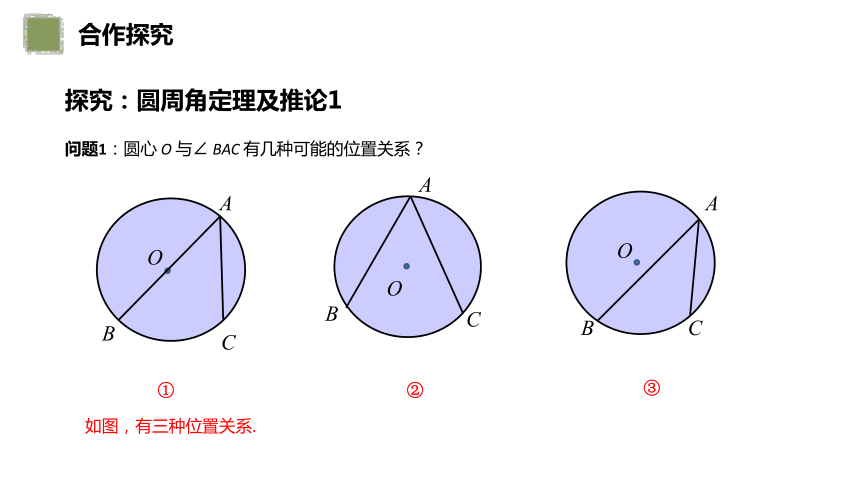
问题1:圆心 O 与∠ BAC 有几种可能的位置关系?
A
B
C
O
①
A
B
C
O
②
A
B
C
O
③
如图,有三种位置关系.
合作探究
探究:圆周角定理及推论1
A
B
C
O
问题2:如图, AB 是⊙ O 的直径,连接 OC,你发现∠ BOC 与∠ BAC有什么位置关系和数量关系?
证明:( 1)当圆心 O 在∠ BAC 的一条边上时(如图).
在△ OAC 中,
∵ OA = OC,
∴ ∠ CAO =∠ OCA .
∵ ∠ BOC =∠ CAO +∠ OCA,
∴ ∠ BOC = 2∠ CAO .
∴ ∠ BAC =
∠ BOC .
合作探究
探究:圆周角定理及推论1
问题3:
能将问题(2)中的结论推广到图 ② ③ 吗?由此你猜想圆周角与它所对弧上的圆心角有怎样的数量关系?怎样证明你的结论?
A
B
C
O
②
D
合作探究
探究:圆周角定理及推论1
A
B
C
O
③
D
(3)当圆心O在∠BAC的外部时,作直径AD,连接OB、OC.由(1)可得:
归纳小结
归纳以上三种情况的结论,就得到
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
思考:圆周角的度数与它所对的弧的度数有什么关系?
推论1 圆周角的度数等于它所对弧的度数的一半.
典例分析
[例1]
在⊙O 中, ∠AOB = 110°,点 C 在 上. 求∠ ACB 的度数.
拓展
拓展:根据圆心角、弧、弦、弦心距之间的关系定理及圆周角定理可以得出什么结论?
在同圆或等圆中,相等的圆周角所对的弧相等,所对的圆心角相等,所对的弦相等,相等弦上的弦心距也相等.
随堂检测
圆周角定理及推论1 课堂评价测试
同学们要认真答题哦!
随堂检测
1.半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 .
2. 如图,圆心角∠AOB=100°,则∠ACB=_________.
60°或120°
130°
B
C
A
O
3.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O半径是_______.
1
第2题图
第3题图
随堂检测
课堂小结
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
如何证明的?
2. 推论1 圆周角的度数等于它所对弧的度数的一半.
在同圆或等圆中相等的圆周角所对的圆心角相等,所对的弧相等,所对的弦相等,相等弦上的弦心距也相等.
作业布置
详见教材练习题
P84 T1-2
谢
谢
第3章 对圆的进一步认识
九年级上册
3.3 圆周角
第1课时 圆周角定理及推论1
课前小测
1.圆心角的定义
2.圆心角的度数和它所对的弧的度数的关系
顶点在圆心的角叫作圆心角.
圆心角的度数与它所对的弧的度数相等
情境引入
问题:你知道什么是圆周角吗?
情境引入
问题1:如图,点 A, B, C 是⊙ O 上的三个点. 以 A 为端点作射线 AB, AC,得到了一个怎样的角?
问题2:∠ BAC 有什么特征?
∠ BAC 的顶点在圆上,并且它的两边在圆内的部分是圆的两条弦,像这样的角叫做圆周角
情境引入
问题3:圆周角与圆心角有什么不同?
1.顶点的位置不同,圆周角顶点在圆上,圆心角顶点在圆心.
2.边不一样.圆周角边是弦的延长线,圆心角的边是半径的延长线.
情境引入
问题4:观察下图中的各角,其中哪些是圆周角?哪些是圆心角?
圆心角有④中的∠BOC和⑥中的∠BOC.
圆周角有④中的∠A和⑤中的∠A,∠ACB和⑥中的∠A.
情境引入
你知道圆周角有哪些性质吗?
合作探究
探究:圆周角定理及推论1
任意画一个⊙ O,在圆上任意取三个点 A, B, C,连接 AB, AC.
O
合作探究
探究:圆周角定理及推论1
问题1:圆心 O 与∠ BAC 有几种可能的位置关系?
A
B
C
O
①
A
B
C
O
②
A
B
C
O
③
如图,有三种位置关系.
合作探究
探究:圆周角定理及推论1
A
B
C
O
问题2:如图, AB 是⊙ O 的直径,连接 OC,你发现∠ BOC 与∠ BAC有什么位置关系和数量关系?
证明:( 1)当圆心 O 在∠ BAC 的一条边上时(如图).
在△ OAC 中,
∵ OA = OC,
∴ ∠ CAO =∠ OCA .
∵ ∠ BOC =∠ CAO +∠ OCA,
∴ ∠ BOC = 2∠ CAO .
∴ ∠ BAC =
∠ BOC .
合作探究
探究:圆周角定理及推论1
问题3:
能将问题(2)中的结论推广到图 ② ③ 吗?由此你猜想圆周角与它所对弧上的圆心角有怎样的数量关系?怎样证明你的结论?
A
B
C
O
②
D
合作探究
探究:圆周角定理及推论1
A
B
C
O
③
D
(3)当圆心O在∠BAC的外部时,作直径AD,连接OB、OC.由(1)可得:
归纳小结
归纳以上三种情况的结论,就得到
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
思考:圆周角的度数与它所对的弧的度数有什么关系?
推论1 圆周角的度数等于它所对弧的度数的一半.
典例分析
[例1]
在⊙O 中, ∠AOB = 110°,点 C 在 上. 求∠ ACB 的度数.
拓展
拓展:根据圆心角、弧、弦、弦心距之间的关系定理及圆周角定理可以得出什么结论?
在同圆或等圆中,相等的圆周角所对的弧相等,所对的圆心角相等,所对的弦相等,相等弦上的弦心距也相等.
随堂检测
圆周角定理及推论1 课堂评价测试
同学们要认真答题哦!
随堂检测
1.半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 .
2. 如图,圆心角∠AOB=100°,则∠ACB=_________.
60°或120°
130°
B
C
A
O
3.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O半径是_______.
1
第2题图
第3题图
随堂检测
课堂小结
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
如何证明的?
2. 推论1 圆周角的度数等于它所对弧的度数的一半.
在同圆或等圆中相等的圆周角所对的圆心角相等,所对的弧相等,所对的弦相等,相等弦上的弦心距也相等.
作业布置
详见教材练习题
P84 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
