3.3第2课时 圆周角定理的推论2,3,4 课件(共23张PPT) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 3.3第2课时 圆周角定理的推论2,3,4 课件(共23张PPT) 2025-2026学年数学青岛版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:48:49 | ||
图片预览




文档简介
(共23张PPT)
第3章 对圆的进一步认识
九年级上册
3.3 圆周角
第2课时 圆周角定理的推论2,3,4
课前小测
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
圆周角定理的内容是什么?
2. 圆周角定理推论1的内容是什么?
推论1 圆周角的度数等于它所对弧的度数的一半.
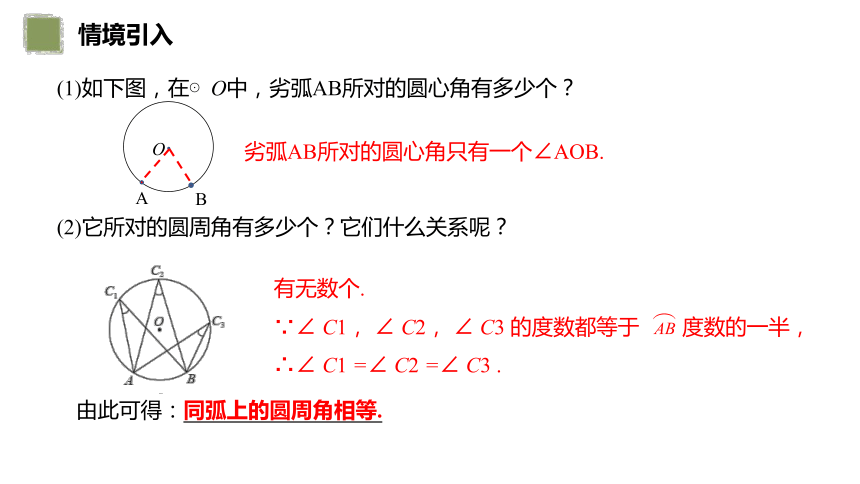
情境引入
O
A
B
(1)如下图,在⊙O中,劣弧AB所对的圆心角有多少个?
劣弧AB所对的圆心角只有一个∠AOB.
(2)它所对的圆周角有多少个?它们什么关系呢?
由此可得:同弧上的圆周角相等.
有无数个.
∵∠ C1, ∠ C2, ∠ C3 的度数都等于 度数的一半,
∴∠ C1 =∠ C2 =∠ C3 .
情境引入
相等的弧所对的圆周角什么关系呢?
合作探究
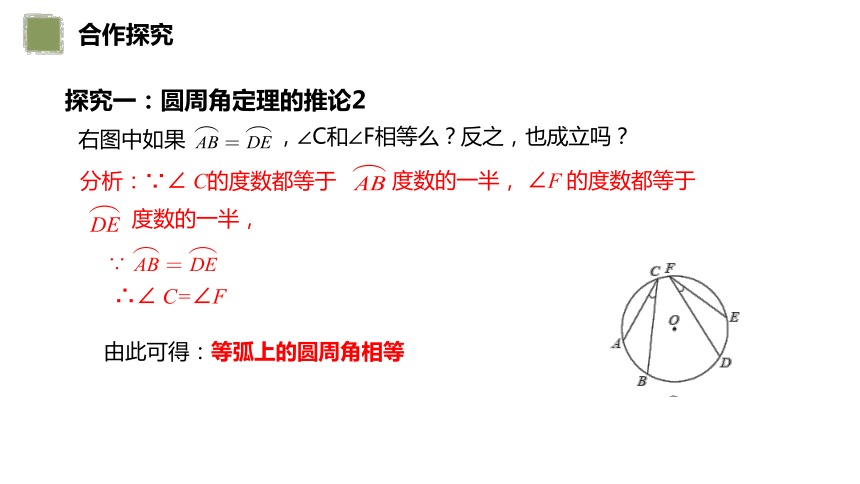
探究一:圆周角定理的推论2
右图中如果
,∠C和∠F相等么?反之,也成立吗?
分析:∵∠ C的度数都等于
度数的一半, ∠F 的度数都等于
度数的一半,
∴∠ C=∠F
∵
由此可得:等弧上的圆周角相等
合作探究
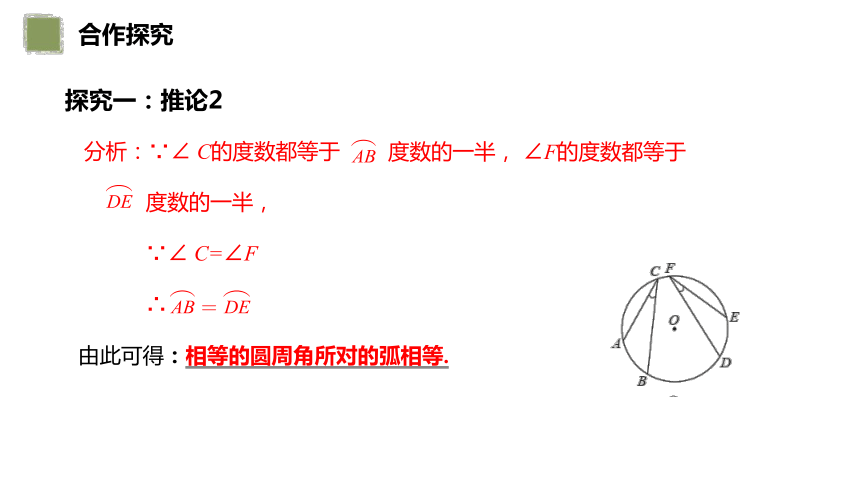
探究一:推论2
分析:∵∠ C的度数都等于
度数的一半, ∠F的度数都等于
度数的一半,
∵∠ C=∠F
∴
由此可得:相等的圆周角所对的弧相等.
归纳小结
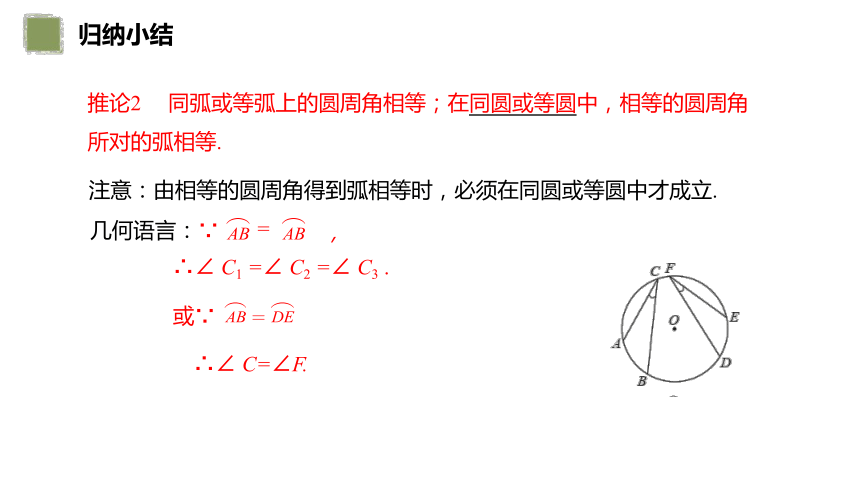
推论2 同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
注意:由相等的圆周角得到弧相等时,必须在同圆或等圆中才成立.
或∵
∴∠ C=∠F.
,
几何语言:∵
=
∴∠ C1 =∠ C2 =∠ C3 .
合作探究
探究二:推论3
(1)在⊙O 中,AB是圆的直径, 它所对的圆周角∠ACB 的度数是多少?为什么?
分析:因为直径AB分⊙O为两个半圆,半圆的度数是180°,
所以∠ACB=
.
由此可得:直径所对的圆周角是直角.
合作探究
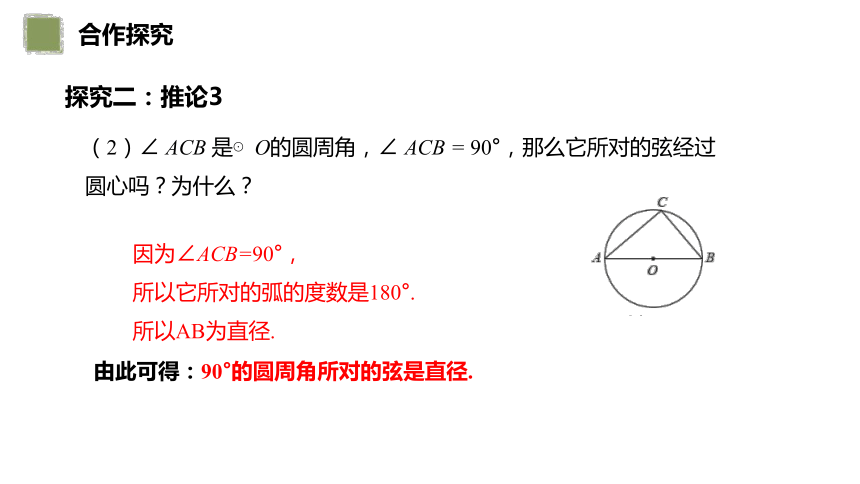
探究二:推论3
(2)∠ ACB 是⊙O的圆周角,∠ ACB = 90°,那么它所对的弦经过圆心吗?为什么?
因为∠ACB=90°,
所以它所对的弧的度数是180°.
所以AB为直径.
由此可得:90°的圆周角所对的弦是直径.
归纳小结
推论3 直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
几何语言:∵AB是直径,∴∠C=90°.
逆定理:∵∠C=90°,∴AB是直径.
典例分析
[例1]
如下图, AD是△ABC 的高,AE是△ABC 的外接圆直径,点O为
圆心.△ADC与△ABE相似吗?说明理由
解 △ ADC ∽△ ABE . 理由如下:
∵ AE 为⊙ O 的直径,∴ ∠ ABE = 90°.
∵ AD⊥ BC,∴ ∠ ADC = 90°. ∠ ADC = ∠ ABE .
∵ ∠ ACD =∠ AEB,
∴△ ADC ∽△ ABE .
探究二:推论3
同弧或等弧上的圆周角相等是在圆内判断角的相等关系的重要依据.
已知直径通常作直径所对的圆周角,从而得到直角三角形,反之有直角作直径.
探究三:推论4
典例分析
如下图,像这样,所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 在图中,四边形 ABCD 是⊙O的内接四边形,⊙O是四边形 ABCD 的外接圆.
探究三:推论4
典例分析
问题:∠ A 与∠ C 具有怎样的数量关系? ∠ B 与∠ D 也具有这样的数量关系吗?
分析:因为
与
由圆周角定理可知, ∠ A +∠ C = 180° .
同理, ∠ B +∠ D = 180° .
归纳总结:推论4 圆内接四边形的对角互补.
的度数之和为360°,
探究三:推论4
[例2]
典例分析
如下图,四边形ABCD内接于⊙O,已知∠BOD = 140°,求∠C的度数.
探究三:推论4
[例3]
典例分析
如下图,△ABC 内接于⊙ O,D,F 分别是
与
上的点, ,
连接 AF 并延长交 CB 的延长线于点 E,连接 AD,CD,
求证: ∠ CAD =∠ E .
证明 ∵
,∴ ∠ BAE =∠ ACD .
∵四边形 ABCD 是⊙ O 的内接四边形,
∴ ∠ ABC +∠ D = 180°.
∵ ∠ ABC +∠ ABE = 180°,
∴ ∠ ABE =∠ D ,∴△ CDA ∽△ ABE .
∴ ∠ CAD =∠ E .
拓展
推论4的拓展:圆内接四边形的一个外角等于它的内对角.
E
如图,四边形ABCD内接于⊙O,求证:∠CBE=∠ADC.
证明∵四边形 ABCD 内接于⊙ O,
∴ ∠ ADC +∠ ABC = 180°.
又∵∠ CBE +∠ ABC = 180°,
∴∠CBE=∠ADC.
随堂检测
圆周角定理推论2、3、4
课堂评价测试
同学们要认真答题哦!
随堂检测
B
C
随堂检测
8
C
随堂检测
5.如图,AB是半圆O的直径,AE为弦,C 为
BC交AE于点G.求证:AF=FC.
的中点,CD⊥AB于点D,交AE于点F,
证明:∵点C是的中点,
∴∠B=∠CAE,
∵AB是⊙O的直径,∴∠ACB=90°,
即∠ACF+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,∴∠B=∠ACF
∴∠B=∠CAF=∠ACF,∴AF=FC.
课堂小结
推论2 同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
推论3 直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
推论4 圆内接四边形的对角互补.
推论4的拓展:圆内接四边形的一个外角等于它的内对角.
这三个推论都是圆中证角或边的最常用的,见到圆周角去找它所对的弧,从而再去找弧所对的圆周角有哪些,已知直径,首先第一反应是找直角.
作业布置
详见教材练习题
P89 T1-2
P87 T1-2
谢
谢
第3章 对圆的进一步认识
九年级上册
3.3 圆周角
第2课时 圆周角定理的推论2,3,4
课前小测
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
圆周角定理的内容是什么?
2. 圆周角定理推论1的内容是什么?
推论1 圆周角的度数等于它所对弧的度数的一半.
情境引入
O
A
B
(1)如下图,在⊙O中,劣弧AB所对的圆心角有多少个?
劣弧AB所对的圆心角只有一个∠AOB.
(2)它所对的圆周角有多少个?它们什么关系呢?
由此可得:同弧上的圆周角相等.
有无数个.
∵∠ C1, ∠ C2, ∠ C3 的度数都等于 度数的一半,
∴∠ C1 =∠ C2 =∠ C3 .
情境引入
相等的弧所对的圆周角什么关系呢?
合作探究
探究一:圆周角定理的推论2
右图中如果
,∠C和∠F相等么?反之,也成立吗?
分析:∵∠ C的度数都等于
度数的一半, ∠F 的度数都等于
度数的一半,
∴∠ C=∠F
∵
由此可得:等弧上的圆周角相等
合作探究
探究一:推论2
分析:∵∠ C的度数都等于
度数的一半, ∠F的度数都等于
度数的一半,
∵∠ C=∠F
∴
由此可得:相等的圆周角所对的弧相等.
归纳小结
推论2 同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
注意:由相等的圆周角得到弧相等时,必须在同圆或等圆中才成立.
或∵
∴∠ C=∠F.
,
几何语言:∵
=
∴∠ C1 =∠ C2 =∠ C3 .
合作探究
探究二:推论3
(1)在⊙O 中,AB是圆的直径, 它所对的圆周角∠ACB 的度数是多少?为什么?
分析:因为直径AB分⊙O为两个半圆,半圆的度数是180°,
所以∠ACB=
.
由此可得:直径所对的圆周角是直角.
合作探究
探究二:推论3
(2)∠ ACB 是⊙O的圆周角,∠ ACB = 90°,那么它所对的弦经过圆心吗?为什么?
因为∠ACB=90°,
所以它所对的弧的度数是180°.
所以AB为直径.
由此可得:90°的圆周角所对的弦是直径.
归纳小结
推论3 直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
几何语言:∵AB是直径,∴∠C=90°.
逆定理:∵∠C=90°,∴AB是直径.
典例分析
[例1]
如下图, AD是△ABC 的高,AE是△ABC 的外接圆直径,点O为
圆心.△ADC与△ABE相似吗?说明理由
解 △ ADC ∽△ ABE . 理由如下:
∵ AE 为⊙ O 的直径,∴ ∠ ABE = 90°.
∵ AD⊥ BC,∴ ∠ ADC = 90°. ∠ ADC = ∠ ABE .
∵ ∠ ACD =∠ AEB,
∴△ ADC ∽△ ABE .
探究二:推论3
同弧或等弧上的圆周角相等是在圆内判断角的相等关系的重要依据.
已知直径通常作直径所对的圆周角,从而得到直角三角形,反之有直角作直径.
探究三:推论4
典例分析
如下图,像这样,所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆. 在图中,四边形 ABCD 是⊙O的内接四边形,⊙O是四边形 ABCD 的外接圆.
探究三:推论4
典例分析
问题:∠ A 与∠ C 具有怎样的数量关系? ∠ B 与∠ D 也具有这样的数量关系吗?
分析:因为
与
由圆周角定理可知, ∠ A +∠ C = 180° .
同理, ∠ B +∠ D = 180° .
归纳总结:推论4 圆内接四边形的对角互补.
的度数之和为360°,
探究三:推论4
[例2]
典例分析
如下图,四边形ABCD内接于⊙O,已知∠BOD = 140°,求∠C的度数.
探究三:推论4
[例3]
典例分析
如下图,△ABC 内接于⊙ O,D,F 分别是
与
上的点, ,
连接 AF 并延长交 CB 的延长线于点 E,连接 AD,CD,
求证: ∠ CAD =∠ E .
证明 ∵
,∴ ∠ BAE =∠ ACD .
∵四边形 ABCD 是⊙ O 的内接四边形,
∴ ∠ ABC +∠ D = 180°.
∵ ∠ ABC +∠ ABE = 180°,
∴ ∠ ABE =∠ D ,∴△ CDA ∽△ ABE .
∴ ∠ CAD =∠ E .
拓展
推论4的拓展:圆内接四边形的一个外角等于它的内对角.
E
如图,四边形ABCD内接于⊙O,求证:∠CBE=∠ADC.
证明∵四边形 ABCD 内接于⊙ O,
∴ ∠ ADC +∠ ABC = 180°.
又∵∠ CBE +∠ ABC = 180°,
∴∠CBE=∠ADC.
随堂检测
圆周角定理推论2、3、4
课堂评价测试
同学们要认真答题哦!
随堂检测
B
C
随堂检测
8
C
随堂检测
5.如图,AB是半圆O的直径,AE为弦,C 为
BC交AE于点G.求证:AF=FC.
的中点,CD⊥AB于点D,交AE于点F,
证明:∵点C是的中点,
∴∠B=∠CAE,
∵AB是⊙O的直径,∴∠ACB=90°,
即∠ACF+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,∴∠B=∠ACF
∴∠B=∠CAF=∠ACF,∴AF=FC.
课堂小结
推论2 同弧或等弧上的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
推论3 直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
推论4 圆内接四边形的对角互补.
推论4的拓展:圆内接四边形的一个外角等于它的内对角.
这三个推论都是圆中证角或边的最常用的,见到圆周角去找它所对的弧,从而再去找弧所对的圆周角有哪些,已知直径,首先第一反应是找直角.
作业布置
详见教材练习题
P89 T1-2
P87 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
