3.6 弧长及扇形面积的计算 课件(共21张PPT) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 3.6 弧长及扇形面积的计算 课件(共21张PPT) 2025-2026学年数学青岛版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:51:27 | ||
图片预览








文档简介
(共21张PPT)
第3章 对圆的进一步认识
九年级上册
3.6 弧长及扇形面积的计算
课前小测
圆的周长公式是什么?
C=2r(d是直径,r是半径)
2.圆的面积公式是什么?
S=r2(r是半径)
3.什么是扇形?
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
情境引入
弧是圆周的一部分,扇形是圆的一部分,那么弧长与扇形面积应怎样计算?
它们与圆的周长、圆的面积之间有怎样的关系呢?
合作探究
探究一: 弧长的计算
半径为r的⊙O 中
(1)360°的圆心角所对的弧长是圆周长为_____
(2)1°的圆心角所对的弧长为_______.
(3)2°的圆心角所对的弧长为_______.
(4)3°的圆心角所对的弧长为_______.
(5)n°的圆心角所对的弧长为_______.
2r
合作探究
探究一: 弧长的计算
归纳总结:弧长计算公式
在半径为r的圆中,n°的圆心角所对的弧长是
n代表n°的圆心角,是1°的倍数,不带单位.
典例分析
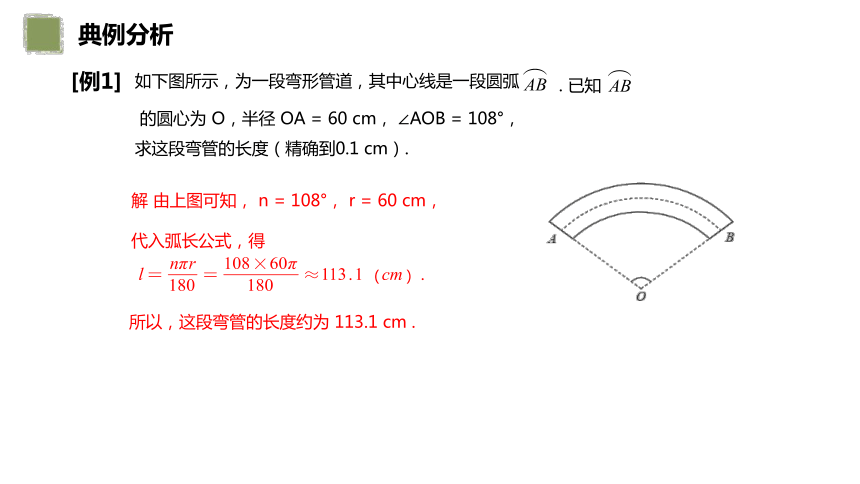
[例1]
如下图所示,为一段弯形管道,其中心线是一段圆弧
. 已知
的圆心为 O,半径 OA = 60 cm, ∠AOB = 108°,
求这段弯管的长度(精确到0.1 cm).
解 由上图可知, n = 108°, r = 60 cm,
代入弧长公式,得
所以,这段弯管的长度约为 113.1 cm .
合作探究
探究二: 扇形面积的计算
问题1:在半径为r的圆中.
(1)360°的圆心角所对的是整个圆,圆的面积为______
(2)1°的圆心角所对的扇形面积为_______.
(3)2°的圆心角所对的扇形面积为_______.
(4)3°的圆心角所对的扇形面积为_______.
(5)n°的圆心角所对的扇形面积为_______.
r2
合作探究
探究二: 扇形面积的计算
扇形面积公式
在半径为r的圆中,n°的圆心角所对的扇形面积是
合作探究
探究二: 扇形面积的计算
问题2:如果已知⊙ O 的半径 r 和扇形的弧长 l,怎样用 l 与 r 表示这段弧所在的扇形的面积呢?
因为扇形的弧长
,所以
于是
归纳小结
第一个扇形面积公式是扇形圆心角度数,扇形半径以及扇形面积的关系;
第二个揭示的是扇形面积与扇形半径,弧长之间的数量关系,为了便于记忆公式,把扇形看作三角形,把l看作底,r看作高,把扇形面积公式当作三角形来记忆.
在做题时,由已知条件选择合适的公式求解.
典例分析
[例2]
如图,一把扇形纸扇完全打开后,外侧两竹条 AB 与 AC 的夹角为 120°, AB 的长为 30 cm,竹条 AB 上贴纸部分 BD 的宽为 20 cm . 求扇子的一面上贴纸部分的面积(精确到 0.1 cm2).
解:由图可知,扇形的圆心为 A,圆心角 n = 120°, AB = 30 cm, BD = 20 cm,图上贴纸部分的面积等于两个扇形面积的差. 由扇形的面积公式,贴纸部分的面积为
所以,扇子的一面上贴纸部分的面积约为 837.8 cm2 .
归纳小结
例1要审题明确题意,理解所求的弯管的长度就是中心线弧AB的长度,要注意题目精确度的要求.
例2找出解题思路,贴纸部分的面积是两个扇形面积的差,学生自行完成解题过程.
拓展
已知扇形 AOB 的半径为 r, ∠ AOB = 90°,以弦 AB为直径作半圆,得到下图 . 你会求图中“新月形”(阴影部分)的面积吗?试一试.
随堂检测
弧长及扇形面积的计算
课堂评价测试
同学们要认真答题哦!
随堂检测
.
随堂检测
3.如图,E是半径为2cm的圆O的直径CD延长线上的一点,AB∥CD且
AB=OD,则阴影部分的面积是______.
随堂检测
4. 如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm.
A
A. 4 B. C. 8 D.
随堂检测
5.如图,四边形ABCD是菱形,,,扇形BEF的半径为2,圆心角为,则图中阴影部分的面积是
A. B. C. D.
A
课堂小结
1.在半径为r的圆中,n°的圆心角所对的弧长是
2.在半径为r的圆中,n°的圆心角所对的扇形面积是
已知圆的半径 r 和扇形的弧长 l,扇形面积
3.不规则图形的面积:一般用等积法、割补法、拼凑法.
作业布置
详见教材练习题
P107 T1-2
谢
谢
第3章 对圆的进一步认识
九年级上册
3.6 弧长及扇形面积的计算
课前小测
圆的周长公式是什么?
C=2r(d是直径,r是半径)
2.圆的面积公式是什么?
S=r2(r是半径)
3.什么是扇形?
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
情境引入
弧是圆周的一部分,扇形是圆的一部分,那么弧长与扇形面积应怎样计算?
它们与圆的周长、圆的面积之间有怎样的关系呢?
合作探究
探究一: 弧长的计算
半径为r的⊙O 中
(1)360°的圆心角所对的弧长是圆周长为_____
(2)1°的圆心角所对的弧长为_______.
(3)2°的圆心角所对的弧长为_______.
(4)3°的圆心角所对的弧长为_______.
(5)n°的圆心角所对的弧长为_______.
2r
合作探究
探究一: 弧长的计算
归纳总结:弧长计算公式
在半径为r的圆中,n°的圆心角所对的弧长是
n代表n°的圆心角,是1°的倍数,不带单位.
典例分析
[例1]
如下图所示,为一段弯形管道,其中心线是一段圆弧
. 已知
的圆心为 O,半径 OA = 60 cm, ∠AOB = 108°,
求这段弯管的长度(精确到0.1 cm).
解 由上图可知, n = 108°, r = 60 cm,
代入弧长公式,得
所以,这段弯管的长度约为 113.1 cm .
合作探究
探究二: 扇形面积的计算
问题1:在半径为r的圆中.
(1)360°的圆心角所对的是整个圆,圆的面积为______
(2)1°的圆心角所对的扇形面积为_______.
(3)2°的圆心角所对的扇形面积为_______.
(4)3°的圆心角所对的扇形面积为_______.
(5)n°的圆心角所对的扇形面积为_______.
r2
合作探究
探究二: 扇形面积的计算
扇形面积公式
在半径为r的圆中,n°的圆心角所对的扇形面积是
合作探究
探究二: 扇形面积的计算
问题2:如果已知⊙ O 的半径 r 和扇形的弧长 l,怎样用 l 与 r 表示这段弧所在的扇形的面积呢?
因为扇形的弧长
,所以
于是
归纳小结
第一个扇形面积公式是扇形圆心角度数,扇形半径以及扇形面积的关系;
第二个揭示的是扇形面积与扇形半径,弧长之间的数量关系,为了便于记忆公式,把扇形看作三角形,把l看作底,r看作高,把扇形面积公式当作三角形来记忆.
在做题时,由已知条件选择合适的公式求解.
典例分析
[例2]
如图,一把扇形纸扇完全打开后,外侧两竹条 AB 与 AC 的夹角为 120°, AB 的长为 30 cm,竹条 AB 上贴纸部分 BD 的宽为 20 cm . 求扇子的一面上贴纸部分的面积(精确到 0.1 cm2).
解:由图可知,扇形的圆心为 A,圆心角 n = 120°, AB = 30 cm, BD = 20 cm,图上贴纸部分的面积等于两个扇形面积的差. 由扇形的面积公式,贴纸部分的面积为
所以,扇子的一面上贴纸部分的面积约为 837.8 cm2 .
归纳小结
例1要审题明确题意,理解所求的弯管的长度就是中心线弧AB的长度,要注意题目精确度的要求.
例2找出解题思路,贴纸部分的面积是两个扇形面积的差,学生自行完成解题过程.
拓展
已知扇形 AOB 的半径为 r, ∠ AOB = 90°,以弦 AB为直径作半圆,得到下图 . 你会求图中“新月形”(阴影部分)的面积吗?试一试.
随堂检测
弧长及扇形面积的计算
课堂评价测试
同学们要认真答题哦!
随堂检测
.
随堂检测
3.如图,E是半径为2cm的圆O的直径CD延长线上的一点,AB∥CD且
AB=OD,则阴影部分的面积是______.
随堂检测
4. 如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm.
A
A. 4 B. C. 8 D.
随堂检测
5.如图,四边形ABCD是菱形,,,扇形BEF的半径为2,圆心角为,则图中阴影部分的面积是
A. B. C. D.
A
课堂小结
1.在半径为r的圆中,n°的圆心角所对的弧长是
2.在半径为r的圆中,n°的圆心角所对的扇形面积是
已知圆的半径 r 和扇形的弧长 l,扇形面积
3.不规则图形的面积:一般用等积法、割补法、拼凑法.
作业布置
详见教材练习题
P107 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
