3.7 正多边形与圆 课件 2025-2026学年数学青岛版九年级上册(共23张PPT)
文档属性
| 名称 | 3.7 正多边形与圆 课件 2025-2026学年数学青岛版九年级上册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:44:44 | ||
图片预览








文档简介
(共23张PPT)
第3章 对圆的进一步认识
九年级上册
3.7 正多边形与圆
课前小测
1.三角形外心的性质?内心的性质?
3.你还记得什么叫正多边形吗?说出你常见的几种正多边形.
外角和恒等于360°.
各边相等、各角也相等的多边形叫作正多边形.
2.n边形的内角和是多少?外角和呢?
三角形的外心是三边垂直平分线的交点,到三个顶点的距离相等;
内心是三条角平分线的交点,到三边的距离相等.
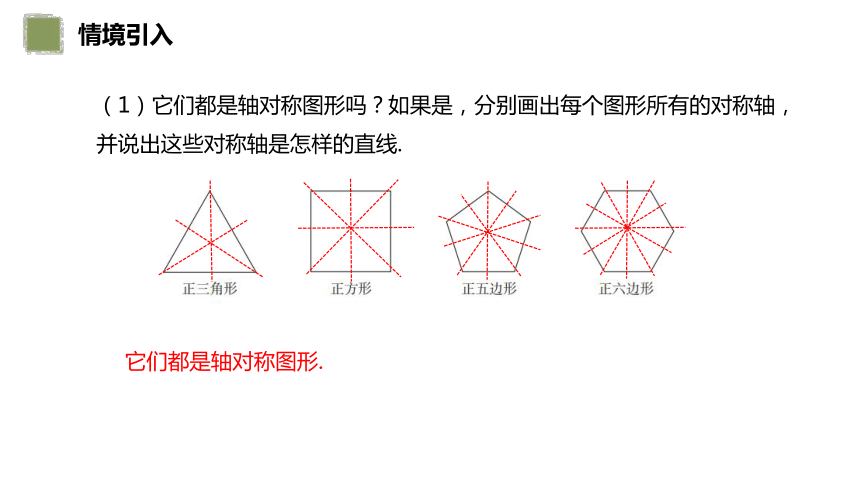
情境引入
(1)它们都是轴对称图形吗?如果是,分别画出每个图形所有的对称轴,
并说出这些对称轴是怎样的直线.
它们都是轴对称图形.
合作探究
探究一: 正多边形的对称性和有关概念
一.正多边形的轴对称性
(1)正三角形有几条对称轴?正四边形、正五边形、正六边形呢?由此你能猜测正 n 边形有几条对称轴吗?各条对称轴有怎样的特征?由此猜测正多边形有什么性质?
正三角形有3条对称轴,正四边形有4条对称轴,正五边形有5条对称轴,正六边形有6条对称轴,由此猜测正n边形有n条对称轴。
正多边形的各条对称轴相交于一点,这点到正多边形的各个顶点的距离相等,到各边的距离也相等.
合作探究
探究一: 正多边形的对称性和有关概念
(2)利用尺规分别画出正方形、正六边形的外接圆和内切圆,它们的外接圆与内切圆有什么特征?你猜测正多边形都有外接圆和内切圆吗?如果有,它们的外接圆与内切圆有什么特征?
任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆,圆心
是各对称轴的交点.
合作探究
探究一:定义
正多边形的外接圆和内切圆的公共圆心叫做正多边形的中心. 如图,圆心O是正方形和正六边形的中心.
外接圆的半径叫做正多边形的半径.如图1,OA、OB是正方形的半径,图2中OA、OB是正六边形的半径.
内切圆的半径叫做正多方形的边心距.图1中OP是正方形的边心距;图2中OP是正六边形的边心距.
正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角,
正 n 边形的每个中心角都等于 .
图1中正方形的中心角是∠AOB=90°;图2中正六边形的中心角是∠AOB=60°.
图1
图2
(1)正多边形的中心:
(2)正多边形的半径:
(3)正多方形的边心距:
(4)正多边形的中心角:
合作探究
三.圆的中心对称性
(1)正 n 边形的 n 条半径把正 n 边形分成了 n 个怎样的图形?相应的边心距把其中每一个图形又分成了两个怎样的图形?
正n边形的n条半径把正n边形分成了n个全等的等腰三角形,每个等腰三角形又被相应的边心距分成了两个全等的直角三角形.
合作探究
(2)如果正三角形的边长为 a,那么它的外接圆的半径 r 和内切圆的半径 d 分别是多少?一般地,如果正 n 边形的边长为 an,半径为 rn,边心距为 dn,这三个量之间有什么关系?
三.圆的中心对称性
合作探究
(3)以正 n 边形的中心 O 为旋转中心,将正 n 边形旋转 ,
你能得到什么结论?
跟原图形重合.
三.圆的中心对称性
合作探究
(4)正 n 边形是中心对称图形吗?
当 n 为偶数时,正 n 边形是中心对称图形,它的中心 O 是对称中心. 当 n 为奇数时,正n边形不是中心对称图形.
三.圆的中心对称性
典例分析
[例1]
一个正六边形花坛的半径为 R,求花坛的边长 a,周长 p 和面积 S .
A
B
C
D
E
F
O
R
G
解 如上图, ABCDEF 为正六边形. 连接OA, OB,作 OG⊥ AB,垂足为点 G,则 OA = OB = R,AB = a .
在等腰三角形 AOB 中,
通过作出正多边形的半径和边心距,可以把正多边形的有关计算问题转化为解
直角三角形的问题.
归纳小结
1.正多边形的轴对称性
(1)正多边形都是轴对称图形,一个正n 边形有n 条对称轴.
(2)正多边形的各条对称轴相交于一点,这点到正多边形的各个顶点的距离相等,到各边的距离也相等.
(3)任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆,圆心
是各对称轴的交点.
2. 正多边形的中心,中心角、半径、边心距的概念及它们之间的关系.
3. 正多边形的中心对称性
当 n 为偶数时,正 n 边形是中心对称图形,它的中心 O 是对称中心. 当 n 为奇数时,正n边形不是中心对称图形.
合作探究
探究二:正多边形的画法
如下图, A, B, C, D, E 都是⊙ O 上的点,且∠ AOB =∠ BOC =∠ COD =∠ DOE .
(3)由(1)与(2),你能将圆周 n 等分吗?你能设计一种画正 n 边形的方法吗?与同学交流.
分析:设计如图所示,画一个圆,记为⊙ O .
(1)用量角器画一个
的圆心角∠ A1OA2;
(2)以点 A2 为圆心,以弦 A2A1 为半径在⊙ O 上截得点 A3 ;
(3)以点 A3 为圆心,以弦 A2A1 为半径在⊙ O 上截得点 A4, 这样继续下去,就可以把⊙ O 分成 n 等份.
(4)顺次连接这 n 个分点,就得到一个正 n 边形.
用这种方法可以画出任意一个正n边形,然而,由量角器所画的角是近似的,因此所画出的正n边形也只能是近似的.
探究二:正多边形的画法
[例2]
典例分析
用直尺和圆规作圆的内接正方形.
已知:⊙O.
求作:⊙O 的内接正方形ABCD .
作法 :(1)过圆心 O 作⊙ O 的任意一条直径 AC .
(2)过点 O 作 AC 的垂线,交⊙ O 于 B, D 两点.
(3)顺次连接点 A, B, C, D, A(如上图).
四边形 ABCD 就是所求作的⊙ O 的内接正方形.
探究二:正多边形的画法
[例3]
典例分析
用直尺和圆规作圆的内接正六边形.
已知:⊙ O.
求作:⊙ O的内接正六边形.
作法 :(1)如图,在⊙ O 上任取一点 A,自点 A 起依次截取长度等于半径 OA 的弦,得到点 B, C, D, E, F .
(2)顺次连接点 A, B, C, D, E, F, A .
六边形 ABCDEF 就是求作的⊙ O 的内接正六边形.
归纳小结
画正多边形有两种作法:
一是求出中心角,在圆中用量角器画出这个中心角,再用圆规在圆上依次截取等弧即可得正多边形.
二是用尺规作图,但只限于一些特殊的正多边形,如例2作正方形,在例2的基础上,再作中心角的角平分线,可以得到正八边形,正十六边形等;如例3的方法作正六边形,取三个点可以作正三角形,作正六边形的中心角的平分线可以得到正十二边形,继续作角平分线可得正二十四边形等.
随堂检测
正多边形与圆 课堂评价测试
同学们要认真答题哦!
随堂检测
A
A
随堂检测
B
B
60°
1
120°
随堂检测
6.在学习圆与正多边形时,马露、高静两位同学设计了一种画圆内接正三角形的方法:
(1)如图,作直径AD;
(2)作半径OD的垂直平分线,交⊙O于B,C两点;
(3)连接AB,AC,那么△ABC为所求的三角形.
请你判断两位同学的作法是否正确,如果正确,请你按照两位同学设计的画法,画出△ABC,然后给出△ABC是等边三角形的证明过程;如果不正确,请说明理由.
A
B
C
D
E
∵BC垂直平分OD,
∴在Rt△OEB中,cos∠BOE= = .
∴∠BOE=60°.由垂径定理得∠COE=∠BOE=60°.
∵AD为直径,∴∠AOB=∠AOC=120°.
∴AB=BC=CA,即△ABC为等边三角形.
解 根据题意画图.两位同学的方法正确.
连BO,CO,设BC交AD于点E.
课堂小结
正多边形是轴对称图形
正多边形的中心对称性
当 n 为偶数时,正 n 边形是中心对称图形,它的中心 O 是对称中心.
当 n 为奇数时,正n边形 不是中心对称图形.
概念:正多边形的半径,边心距,边长,中心,中心角以及它们之间的关系.
4. 正多边形的画法
作业布置
详见教材练习题
P112 T1-2
谢
谢
第3章 对圆的进一步认识
九年级上册
3.7 正多边形与圆
课前小测
1.三角形外心的性质?内心的性质?
3.你还记得什么叫正多边形吗?说出你常见的几种正多边形.
外角和恒等于360°.
各边相等、各角也相等的多边形叫作正多边形.
2.n边形的内角和是多少?外角和呢?
三角形的外心是三边垂直平分线的交点,到三个顶点的距离相等;
内心是三条角平分线的交点,到三边的距离相等.
情境引入
(1)它们都是轴对称图形吗?如果是,分别画出每个图形所有的对称轴,
并说出这些对称轴是怎样的直线.
它们都是轴对称图形.
合作探究
探究一: 正多边形的对称性和有关概念
一.正多边形的轴对称性
(1)正三角形有几条对称轴?正四边形、正五边形、正六边形呢?由此你能猜测正 n 边形有几条对称轴吗?各条对称轴有怎样的特征?由此猜测正多边形有什么性质?
正三角形有3条对称轴,正四边形有4条对称轴,正五边形有5条对称轴,正六边形有6条对称轴,由此猜测正n边形有n条对称轴。
正多边形的各条对称轴相交于一点,这点到正多边形的各个顶点的距离相等,到各边的距离也相等.
合作探究
探究一: 正多边形的对称性和有关概念
(2)利用尺规分别画出正方形、正六边形的外接圆和内切圆,它们的外接圆与内切圆有什么特征?你猜测正多边形都有外接圆和内切圆吗?如果有,它们的外接圆与内切圆有什么特征?
任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆,圆心
是各对称轴的交点.
合作探究
探究一:定义
正多边形的外接圆和内切圆的公共圆心叫做正多边形的中心. 如图,圆心O是正方形和正六边形的中心.
外接圆的半径叫做正多边形的半径.如图1,OA、OB是正方形的半径,图2中OA、OB是正六边形的半径.
内切圆的半径叫做正多方形的边心距.图1中OP是正方形的边心距;图2中OP是正六边形的边心距.
正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角,
正 n 边形的每个中心角都等于 .
图1中正方形的中心角是∠AOB=90°;图2中正六边形的中心角是∠AOB=60°.
图1
图2
(1)正多边形的中心:
(2)正多边形的半径:
(3)正多方形的边心距:
(4)正多边形的中心角:
合作探究
三.圆的中心对称性
(1)正 n 边形的 n 条半径把正 n 边形分成了 n 个怎样的图形?相应的边心距把其中每一个图形又分成了两个怎样的图形?
正n边形的n条半径把正n边形分成了n个全等的等腰三角形,每个等腰三角形又被相应的边心距分成了两个全等的直角三角形.
合作探究
(2)如果正三角形的边长为 a,那么它的外接圆的半径 r 和内切圆的半径 d 分别是多少?一般地,如果正 n 边形的边长为 an,半径为 rn,边心距为 dn,这三个量之间有什么关系?
三.圆的中心对称性
合作探究
(3)以正 n 边形的中心 O 为旋转中心,将正 n 边形旋转 ,
你能得到什么结论?
跟原图形重合.
三.圆的中心对称性
合作探究
(4)正 n 边形是中心对称图形吗?
当 n 为偶数时,正 n 边形是中心对称图形,它的中心 O 是对称中心. 当 n 为奇数时,正n边形不是中心对称图形.
三.圆的中心对称性
典例分析
[例1]
一个正六边形花坛的半径为 R,求花坛的边长 a,周长 p 和面积 S .
A
B
C
D
E
F
O
R
G
解 如上图, ABCDEF 为正六边形. 连接OA, OB,作 OG⊥ AB,垂足为点 G,则 OA = OB = R,AB = a .
在等腰三角形 AOB 中,
通过作出正多边形的半径和边心距,可以把正多边形的有关计算问题转化为解
直角三角形的问题.
归纳小结
1.正多边形的轴对称性
(1)正多边形都是轴对称图形,一个正n 边形有n 条对称轴.
(2)正多边形的各条对称轴相交于一点,这点到正多边形的各个顶点的距离相等,到各边的距离也相等.
(3)任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆,圆心
是各对称轴的交点.
2. 正多边形的中心,中心角、半径、边心距的概念及它们之间的关系.
3. 正多边形的中心对称性
当 n 为偶数时,正 n 边形是中心对称图形,它的中心 O 是对称中心. 当 n 为奇数时,正n边形不是中心对称图形.
合作探究
探究二:正多边形的画法
如下图, A, B, C, D, E 都是⊙ O 上的点,且∠ AOB =∠ BOC =∠ COD =∠ DOE .
(3)由(1)与(2),你能将圆周 n 等分吗?你能设计一种画正 n 边形的方法吗?与同学交流.
分析:设计如图所示,画一个圆,记为⊙ O .
(1)用量角器画一个
的圆心角∠ A1OA2;
(2)以点 A2 为圆心,以弦 A2A1 为半径在⊙ O 上截得点 A3 ;
(3)以点 A3 为圆心,以弦 A2A1 为半径在⊙ O 上截得点 A4, 这样继续下去,就可以把⊙ O 分成 n 等份.
(4)顺次连接这 n 个分点,就得到一个正 n 边形.
用这种方法可以画出任意一个正n边形,然而,由量角器所画的角是近似的,因此所画出的正n边形也只能是近似的.
探究二:正多边形的画法
[例2]
典例分析
用直尺和圆规作圆的内接正方形.
已知:⊙O.
求作:⊙O 的内接正方形ABCD .
作法 :(1)过圆心 O 作⊙ O 的任意一条直径 AC .
(2)过点 O 作 AC 的垂线,交⊙ O 于 B, D 两点.
(3)顺次连接点 A, B, C, D, A(如上图).
四边形 ABCD 就是所求作的⊙ O 的内接正方形.
探究二:正多边形的画法
[例3]
典例分析
用直尺和圆规作圆的内接正六边形.
已知:⊙ O.
求作:⊙ O的内接正六边形.
作法 :(1)如图,在⊙ O 上任取一点 A,自点 A 起依次截取长度等于半径 OA 的弦,得到点 B, C, D, E, F .
(2)顺次连接点 A, B, C, D, E, F, A .
六边形 ABCDEF 就是求作的⊙ O 的内接正六边形.
归纳小结
画正多边形有两种作法:
一是求出中心角,在圆中用量角器画出这个中心角,再用圆规在圆上依次截取等弧即可得正多边形.
二是用尺规作图,但只限于一些特殊的正多边形,如例2作正方形,在例2的基础上,再作中心角的角平分线,可以得到正八边形,正十六边形等;如例3的方法作正六边形,取三个点可以作正三角形,作正六边形的中心角的平分线可以得到正十二边形,继续作角平分线可得正二十四边形等.
随堂检测
正多边形与圆 课堂评价测试
同学们要认真答题哦!
随堂检测
A
A
随堂检测
B
B
60°
1
120°
随堂检测
6.在学习圆与正多边形时,马露、高静两位同学设计了一种画圆内接正三角形的方法:
(1)如图,作直径AD;
(2)作半径OD的垂直平分线,交⊙O于B,C两点;
(3)连接AB,AC,那么△ABC为所求的三角形.
请你判断两位同学的作法是否正确,如果正确,请你按照两位同学设计的画法,画出△ABC,然后给出△ABC是等边三角形的证明过程;如果不正确,请说明理由.
A
B
C
D
E
∵BC垂直平分OD,
∴在Rt△OEB中,cos∠BOE= = .
∴∠BOE=60°.由垂径定理得∠COE=∠BOE=60°.
∵AD为直径,∴∠AOB=∠AOC=120°.
∴AB=BC=CA,即△ABC为等边三角形.
解 根据题意画图.两位同学的方法正确.
连BO,CO,设BC交AD于点E.
课堂小结
正多边形是轴对称图形
正多边形的中心对称性
当 n 为偶数时,正 n 边形是中心对称图形,它的中心 O 是对称中心.
当 n 为奇数时,正n边形 不是中心对称图形.
概念:正多边形的半径,边心距,边长,中心,中心角以及它们之间的关系.
4. 正多边形的画法
作业布置
详见教材练习题
P112 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
