第10章 数的开方 本章复习课(含答案) 2025-2026学年数学华东师大版(2024)八年级上册
文档属性
| 名称 | 第10章 数的开方 本章复习课(含答案) 2025-2026学年数学华东师大版(2024)八年级上册 | 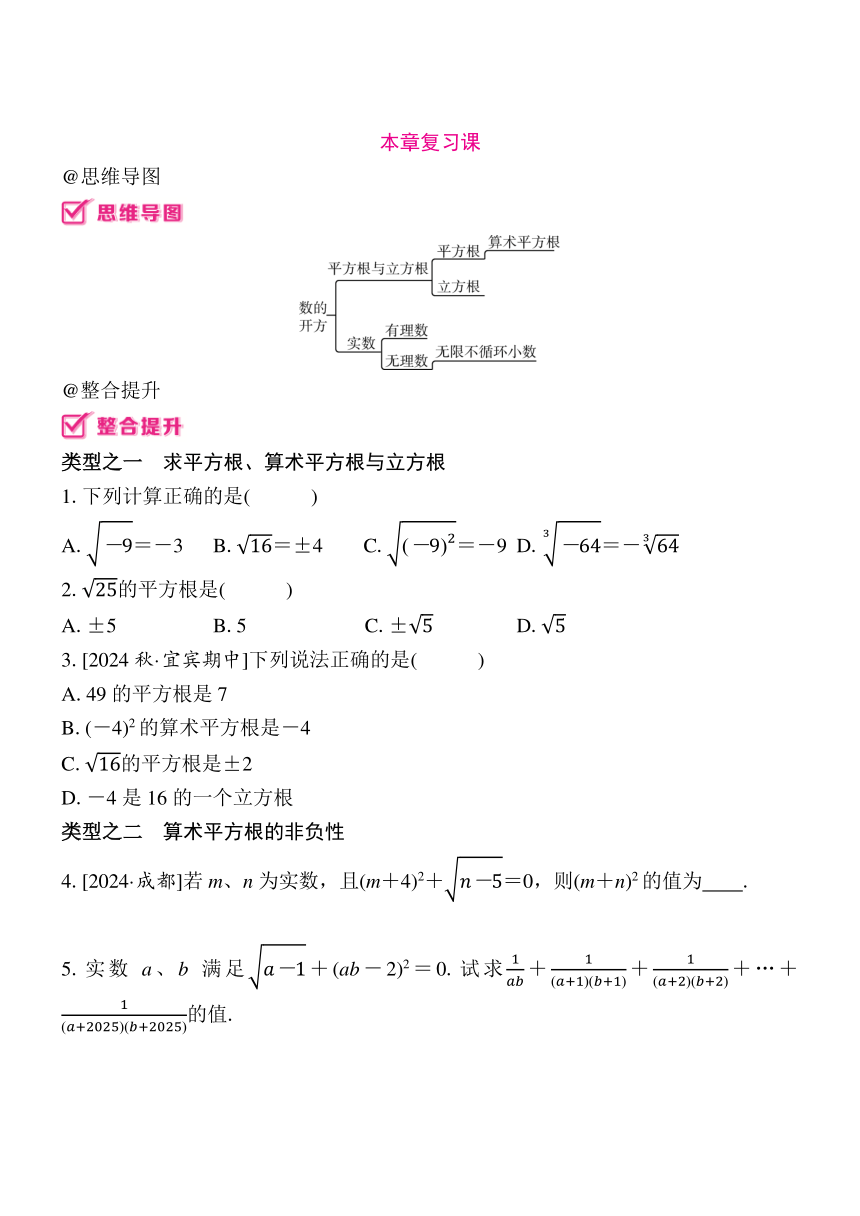 | |
| 格式 | docx | ||
| 文件大小 | 73.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 21:17:00 | ||
图片预览


文档简介
本章复习课
@思维导图
@整合提升
类型之一 求平方根、算术平方根与立方根
1.下列计算正确的是( )
A.=-3 B.=±4 C.=-9 D.=-
2.的平方根是( )
A.±5 B.5 C.± D.
3.[2024秋·宜宾期中]下列说法正确的是( )
A.49的平方根是7
B.(-4)2的算术平方根是-4
C.的平方根是±2
D.-4是16的一个立方根
类型之二 算术平方根的非负性
4.[2024·成都]若m、n为实数,且(m+4)2+=0,则(m+n)2的值为 .
5.实数a、b满足+(ab-2)2=0.试求+++…+的值.
类型之三 实数的有关概念
6.[2024秋·眉山月考]在实数3.1415926,,0,,,-0.,-,0.1010010001…(相邻两个1之间0的个数逐次加1)中,无理数有( )
A.2个 B.3个 C.4个 D.5个
7.化简|-3|,结果正确的是( )
A.-3 B.--3 C.+3 D.3-
8.把下列各数填入它所属的集合内:
-,0,,0.050050005…(相邻两个5之间0的个数逐次加1),,300,-,-|-3.14|,-0..
负数集合:{ ,…};
非负整数集合:{ ,…};
分数集合:{ ,…};
无理数集合:{ ,…}.
类型之四 实数的大小比较
9.[2024·巴中]在0,1,-1,π中,最小的实数是( )
A.0 B.-1 C.1 D.π
10.[2023·扬州]已知a=,b=2,c=,则a、b、c的大小关系是( )
A.b>a>c B.a>c>b C.a>b>c D.b>c>a
11.[2024·山西]比较大小: 2(填“>”“<”或“=”).
12.[2024·滨州]写出一个比大且比小的整数: .
13.如图,实数-,,m在数轴上所对应的点分别为A、B、C,点B关于原点O的对称点为D.若m为整数,则m的值为 .
类型之五 实数的运算
14.计算:
(1)()2-+;
(2)(-2)3×+(-1)2025-;
(3)++-.
类型之六 估算无理数的大小
15.[2024秋·驻马店阶段练习]新定义:若无理数的被开方数T(T为正整数)满足n2<T<(n+1)2(其中n正整数),则n<<n+1,则称无理数的“青一区间”为(n,n+1);同理规定无理数-的“青一区间”为(-n-1,-n).例如,∵22<7<32,∴2<<3,∴的“青一区间”为(2,3),-的“青一区间”为(-3,-2).请解答下列问题:
(1)的“青一区间”是 ;-的“青一区间”是 .
(2)若无理数-(a为正整数)的“青一区间”为(-6,-5),的“青一区间”为(3,4),求的值.
参考答案
【整合提升】
1.D 2.C 3.C 4.1 5.
6.B 7.D 8.-,-|-3.14|,-0.115 0,300 -,,-,-|-3.14|,-0.115 0.050050005…(相邻两个5之间0的个数逐次加1),
9.B 10.C 11.> 12.2(或3) 13.-3
14.(1)-3 (2)-48 (3)2
15.(1)(4,5) (-5,-4) (2)的值为3或.
。
@思维导图
@整合提升
类型之一 求平方根、算术平方根与立方根
1.下列计算正确的是( )
A.=-3 B.=±4 C.=-9 D.=-
2.的平方根是( )
A.±5 B.5 C.± D.
3.[2024秋·宜宾期中]下列说法正确的是( )
A.49的平方根是7
B.(-4)2的算术平方根是-4
C.的平方根是±2
D.-4是16的一个立方根
类型之二 算术平方根的非负性
4.[2024·成都]若m、n为实数,且(m+4)2+=0,则(m+n)2的值为 .
5.实数a、b满足+(ab-2)2=0.试求+++…+的值.
类型之三 实数的有关概念
6.[2024秋·眉山月考]在实数3.1415926,,0,,,-0.,-,0.1010010001…(相邻两个1之间0的个数逐次加1)中,无理数有( )
A.2个 B.3个 C.4个 D.5个
7.化简|-3|,结果正确的是( )
A.-3 B.--3 C.+3 D.3-
8.把下列各数填入它所属的集合内:
-,0,,0.050050005…(相邻两个5之间0的个数逐次加1),,300,-,-|-3.14|,-0..
负数集合:{ ,…};
非负整数集合:{ ,…};
分数集合:{ ,…};
无理数集合:{ ,…}.
类型之四 实数的大小比较
9.[2024·巴中]在0,1,-1,π中,最小的实数是( )
A.0 B.-1 C.1 D.π
10.[2023·扬州]已知a=,b=2,c=,则a、b、c的大小关系是( )
A.b>a>c B.a>c>b C.a>b>c D.b>c>a
11.[2024·山西]比较大小: 2(填“>”“<”或“=”).
12.[2024·滨州]写出一个比大且比小的整数: .
13.如图,实数-,,m在数轴上所对应的点分别为A、B、C,点B关于原点O的对称点为D.若m为整数,则m的值为 .
类型之五 实数的运算
14.计算:
(1)()2-+;
(2)(-2)3×+(-1)2025-;
(3)++-.
类型之六 估算无理数的大小
15.[2024秋·驻马店阶段练习]新定义:若无理数的被开方数T(T为正整数)满足n2<T<(n+1)2(其中n正整数),则n<<n+1,则称无理数的“青一区间”为(n,n+1);同理规定无理数-的“青一区间”为(-n-1,-n).例如,∵22<7<32,∴2<<3,∴的“青一区间”为(2,3),-的“青一区间”为(-3,-2).请解答下列问题:
(1)的“青一区间”是 ;-的“青一区间”是 .
(2)若无理数-(a为正整数)的“青一区间”为(-6,-5),的“青一区间”为(3,4),求的值.
参考答案
【整合提升】
1.D 2.C 3.C 4.1 5.
6.B 7.D 8.-,-|-3.14|,-0.115 0,300 -,,-,-|-3.14|,-0.115 0.050050005…(相邻两个5之间0的个数逐次加1),
9.B 10.C 11.> 12.2(或3) 13.-3
14.(1)-3 (2)-48 (3)2
15.(1)(4,5) (-5,-4) (2)的值为3或.
。
