第12章 全等三角形 质量评估(含答案) 2025-2026学年数学华东师大版(2024)八年级上册
文档属性
| 名称 | 第12章 全等三角形 质量评估(含答案) 2025-2026学年数学华东师大版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览



文档简介
第12章 全等三角形 质量评估
第Ⅰ卷(选择题 共40分)
一、选择题(共10小题,每小题4分,共40分)
1.等腰三角形的底边长与其腰长的比值称为这个等腰三角形的“优美比”.若等腰三角形ABC的周长为20,其中一边长为8,则它的“优美比”为( )
A. B. C.或2 D.或
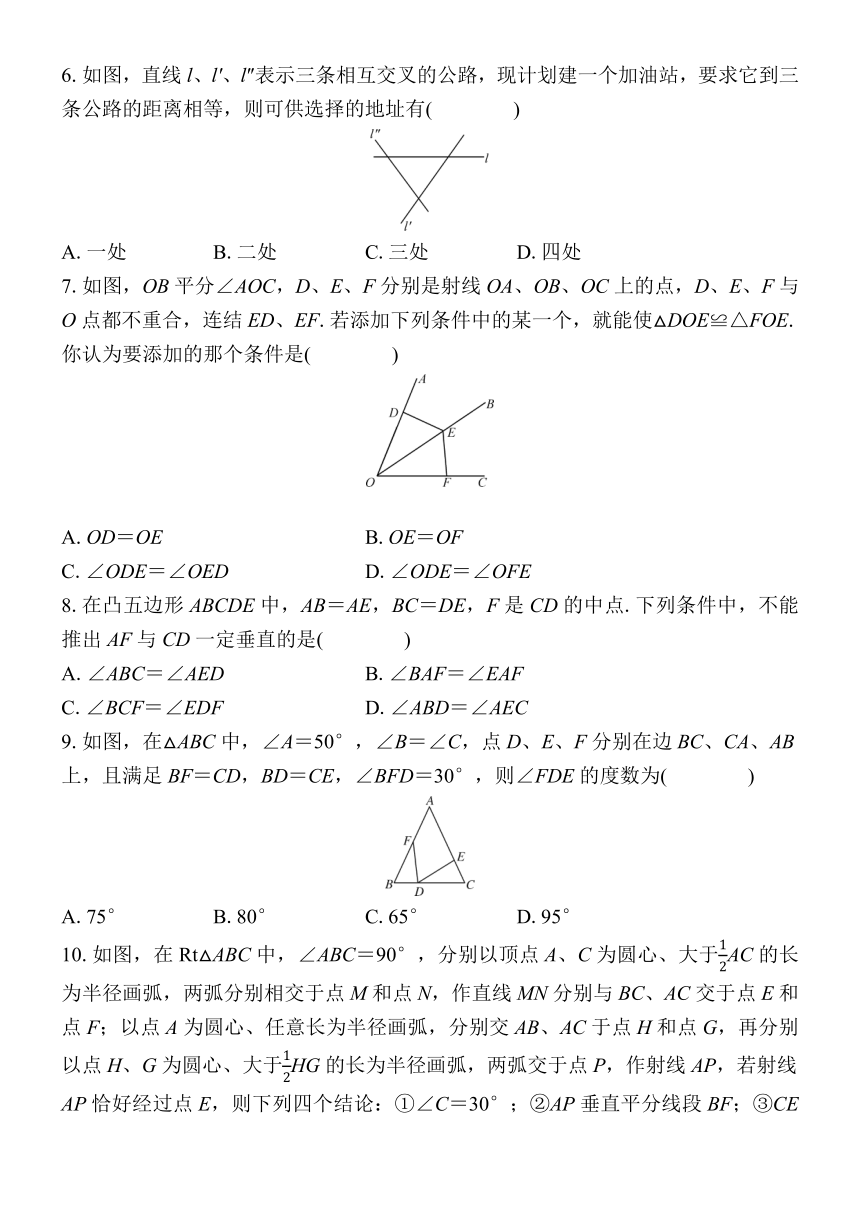
2.如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
A.SSS B.SAS C.AAS D.HL
3.如图,在△ABC中,AB的垂直平分线交AC于点D.如果AC=5cm,BC=4cm,那么△DBC的周长是( )
A.6cm B.7cm C.8cm D.9cm
4.如图,∠E=∠F=90°,∠B=∠C,AE=AF,则下列结论:①∠EAC=∠FAB;②CM=BN;③CD=DN;④△ACN≌△ABM.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
5.如图,在△ABC中,CD⊥AB于点D,BE平分∠ABC交CD于点E.若S△BCE=24,BC=12,则DE的长为( )
A.10 B.7 C.5 D.4
6.如图,直线l、l'、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
7.如图,OB平分∠AOC,D、E、F分别是射线OA、OB、OC上的点,D、E、F与O点都不重合,连结ED、EF.若添加下列条件中的某一个,就能使△DOE≌△FOE.你认为要添加的那个条件是( )
A.OD=OE B.OE=OF
C.∠ODE=∠OED D.∠ODE=∠OFE
8.在凸五边形ABCDE中,AB=AE,BC=DE,F是CD的中点.下列条件中,不能推出AF与CD一定垂直的是( )
A.∠ABC=∠AED B.∠BAF=∠EAF
C.∠BCF=∠EDF D.∠ABD=∠AEC
9.如图,在△ABC中,∠A=50°,∠B=∠C,点D、E、F分别在边BC、CA、AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
A.75° B.80° C.65° D.95°
10.如图,在Rt△ABC中,∠ABC=90°,分别以顶点A、C为圆心、大于AC的长为半径画弧,两弧分别相交于点M和点N,作直线MN分别与BC、AC交于点E和点F;以点A为圆心、任意长为半径画弧,分别交AB、AC于点H和点G,再分别以点H、G为圆心、大于HG的长为半径画弧,两弧交于点P,作射线AP,若射线AP恰好经过点E,则下列四个结论:①∠C=30°;②AP垂直平分线段BF;③CE=2BE;④S△BEF=S△ABC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 共110分)
二、填空题(共6小题,每小题4分,共24分)
11.“全等三角形面积相等”是 命题,其中条件是 ,结论是 .
12.如图,在△ABC中,AB=AC=14cm,AB的垂直平分线MN交AC于点D,且△DBC的周长是24cm,则BC= cm.
13.如图,在△ABC中,∠B=40°,∠C=50°.通过观察尺规作图的痕迹,可以求得∠DAE= °.
14.如图,在四边形ABCD中,AB=BC=BD.设∠ABC=α,则∠ADC= (用含α的代数式表示).
15.如图,AC=AD,∠1=∠2,要使△ABC≌△AED(不添加辅助线),应添加的条件是 (写出一个即可).
16.如图,在△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是 .
三、解答题(共7小题,共86分)
17.(12分)如图,在等边三角形ABC中,BD平分∠ABC,交AC于点D,过点D作DE∥AB交BC于点E,连结AE.求证:AE⊥BC.
18.(12分)某校八年级数学兴趣小组的同学在研究三角形时,把两个大小不同的等腰直角三角板按如图1所示放置,图2是由它抽象出的几何图形,其中点B、C、E在同一条直线上,连结DC.请找出图2中的全等三角形,并加以证明(结论中不得含有未标识的字母).
19.(12分)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连结AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC的长.
20.(12分)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.
(1)求证:BC=DE.
(2)若∠B=30°,∠APC=70°.
①求∠E的度数;
②求证:CP=CE.
21.(12分)如图,在△ABC中,AB=AC,D为CA延长线上的一动点,且DE⊥BC,交AB于点F.
(1)求证:△ADF是等腰三角形.
(2)当F为AB的中点时,DF与EF有怎样的数量关系?请写出结论,并说明理由.
22.(12分)为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河流南岸的点B处,测得河流北岸的一棵树底部点A恰好在点B的正北方向,测量方案如下表.
实践课题 测量河流宽度
测量工具 测量角度的仪器(仪器的高度忽略不计)、标杆、皮尺等.
小组 第一小组 第二小组 第三小组
测量方案 观测者从点B沿正东方向走到点C处,此时恰好测得∠ACB=45°. 观测者从点B沿正东方向走到点E,点O是BE的中点,然后从点E沿垂直于BE的正南方向走,直到A、O、F三点在同一条直线上.
测量 示意图
(1)第一小组认为,河宽AB的长度就是线段 的长度.
(2)第二小组的方案灵感来源于古希腊哲学家泰勒斯,他们认为河宽AB的长度就是线段EF的长度,你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.
(3)请你代表第三小组,设计一个测量方案,把测量方案和测量示意图填入上表,并说明方案的可行性.
23.(14分)【阅读理解】课外兴趣小组活动时,老师提出了如下问题.
如图1,在△ABC中,若AB=8,AC=6,求边BC上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考.
(1)由已知和作图能得到△ADC≌△EDB的理由是 .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】(3)如图2,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF.求证:AC=BF.
参考答案
1.D 2.B 3.D 4.B 5.D 6.D
7.D 8.D 9.C 10.D 11.真 两个三角形全等 它们的面积相等 12.10 13.25
14.180°- 15.∠B=∠E(∠C=∠EDA或AB=AE) 16.90°
17.略
18.△ABE≌△ACD.证明略.
19.(1)略 (2)4cm
20.(1)略 (2)①70° ②略
21.(1)略 (2)结论:DF=2EF.理由略.
22.(1)BC (2)第二小组的方案可行.理由略.
(3)略
23.(1)B (2)C (3)略
。
第Ⅰ卷(选择题 共40分)
一、选择题(共10小题,每小题4分,共40分)
1.等腰三角形的底边长与其腰长的比值称为这个等腰三角形的“优美比”.若等腰三角形ABC的周长为20,其中一边长为8,则它的“优美比”为( )
A. B. C.或2 D.或
2.如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
A.SSS B.SAS C.AAS D.HL
3.如图,在△ABC中,AB的垂直平分线交AC于点D.如果AC=5cm,BC=4cm,那么△DBC的周长是( )
A.6cm B.7cm C.8cm D.9cm
4.如图,∠E=∠F=90°,∠B=∠C,AE=AF,则下列结论:①∠EAC=∠FAB;②CM=BN;③CD=DN;④△ACN≌△ABM.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
5.如图,在△ABC中,CD⊥AB于点D,BE平分∠ABC交CD于点E.若S△BCE=24,BC=12,则DE的长为( )
A.10 B.7 C.5 D.4
6.如图,直线l、l'、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
7.如图,OB平分∠AOC,D、E、F分别是射线OA、OB、OC上的点,D、E、F与O点都不重合,连结ED、EF.若添加下列条件中的某一个,就能使△DOE≌△FOE.你认为要添加的那个条件是( )
A.OD=OE B.OE=OF
C.∠ODE=∠OED D.∠ODE=∠OFE
8.在凸五边形ABCDE中,AB=AE,BC=DE,F是CD的中点.下列条件中,不能推出AF与CD一定垂直的是( )
A.∠ABC=∠AED B.∠BAF=∠EAF
C.∠BCF=∠EDF D.∠ABD=∠AEC
9.如图,在△ABC中,∠A=50°,∠B=∠C,点D、E、F分别在边BC、CA、AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
A.75° B.80° C.65° D.95°
10.如图,在Rt△ABC中,∠ABC=90°,分别以顶点A、C为圆心、大于AC的长为半径画弧,两弧分别相交于点M和点N,作直线MN分别与BC、AC交于点E和点F;以点A为圆心、任意长为半径画弧,分别交AB、AC于点H和点G,再分别以点H、G为圆心、大于HG的长为半径画弧,两弧交于点P,作射线AP,若射线AP恰好经过点E,则下列四个结论:①∠C=30°;②AP垂直平分线段BF;③CE=2BE;④S△BEF=S△ABC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题 共110分)
二、填空题(共6小题,每小题4分,共24分)
11.“全等三角形面积相等”是 命题,其中条件是 ,结论是 .
12.如图,在△ABC中,AB=AC=14cm,AB的垂直平分线MN交AC于点D,且△DBC的周长是24cm,则BC= cm.
13.如图,在△ABC中,∠B=40°,∠C=50°.通过观察尺规作图的痕迹,可以求得∠DAE= °.
14.如图,在四边形ABCD中,AB=BC=BD.设∠ABC=α,则∠ADC= (用含α的代数式表示).
15.如图,AC=AD,∠1=∠2,要使△ABC≌△AED(不添加辅助线),应添加的条件是 (写出一个即可).
16.如图,在△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是 .
三、解答题(共7小题,共86分)
17.(12分)如图,在等边三角形ABC中,BD平分∠ABC,交AC于点D,过点D作DE∥AB交BC于点E,连结AE.求证:AE⊥BC.
18.(12分)某校八年级数学兴趣小组的同学在研究三角形时,把两个大小不同的等腰直角三角板按如图1所示放置,图2是由它抽象出的几何图形,其中点B、C、E在同一条直线上,连结DC.请找出图2中的全等三角形,并加以证明(结论中不得含有未标识的字母).
19.(12分)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连结AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC的长.
20.(12分)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.
(1)求证:BC=DE.
(2)若∠B=30°,∠APC=70°.
①求∠E的度数;
②求证:CP=CE.
21.(12分)如图,在△ABC中,AB=AC,D为CA延长线上的一动点,且DE⊥BC,交AB于点F.
(1)求证:△ADF是等腰三角形.
(2)当F为AB的中点时,DF与EF有怎样的数量关系?请写出结论,并说明理由.
22.(12分)为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河流南岸的点B处,测得河流北岸的一棵树底部点A恰好在点B的正北方向,测量方案如下表.
实践课题 测量河流宽度
测量工具 测量角度的仪器(仪器的高度忽略不计)、标杆、皮尺等.
小组 第一小组 第二小组 第三小组
测量方案 观测者从点B沿正东方向走到点C处,此时恰好测得∠ACB=45°. 观测者从点B沿正东方向走到点E,点O是BE的中点,然后从点E沿垂直于BE的正南方向走,直到A、O、F三点在同一条直线上.
测量 示意图
(1)第一小组认为,河宽AB的长度就是线段 的长度.
(2)第二小组的方案灵感来源于古希腊哲学家泰勒斯,他们认为河宽AB的长度就是线段EF的长度,你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.
(3)请你代表第三小组,设计一个测量方案,把测量方案和测量示意图填入上表,并说明方案的可行性.
23.(14分)【阅读理解】课外兴趣小组活动时,老师提出了如下问题.
如图1,在△ABC中,若AB=8,AC=6,求边BC上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考.
(1)由已知和作图能得到△ADC≌△EDB的理由是 .
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是 .
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
【感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】(3)如图2,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF.求证:AC=BF.
参考答案
1.D 2.B 3.D 4.B 5.D 6.D
7.D 8.D 9.C 10.D 11.真 两个三角形全等 它们的面积相等 12.10 13.25
14.180°- 15.∠B=∠E(∠C=∠EDA或AB=AE) 16.90°
17.略
18.△ABE≌△ACD.证明略.
19.(1)略 (2)4cm
20.(1)略 (2)①70° ②略
21.(1)略 (2)结论:DF=2EF.理由略.
22.(1)BC (2)第二小组的方案可行.理由略.
(3)略
23.(1)B (2)C (3)略
。
