专题3 全等三角形 期末复习 (含答案) 2025-2026学年数学华东师大版(2024)八年级上册
文档属性
| 名称 | 专题3 全等三角形 期末复习 (含答案) 2025-2026学年数学华东师大版(2024)八年级上册 | 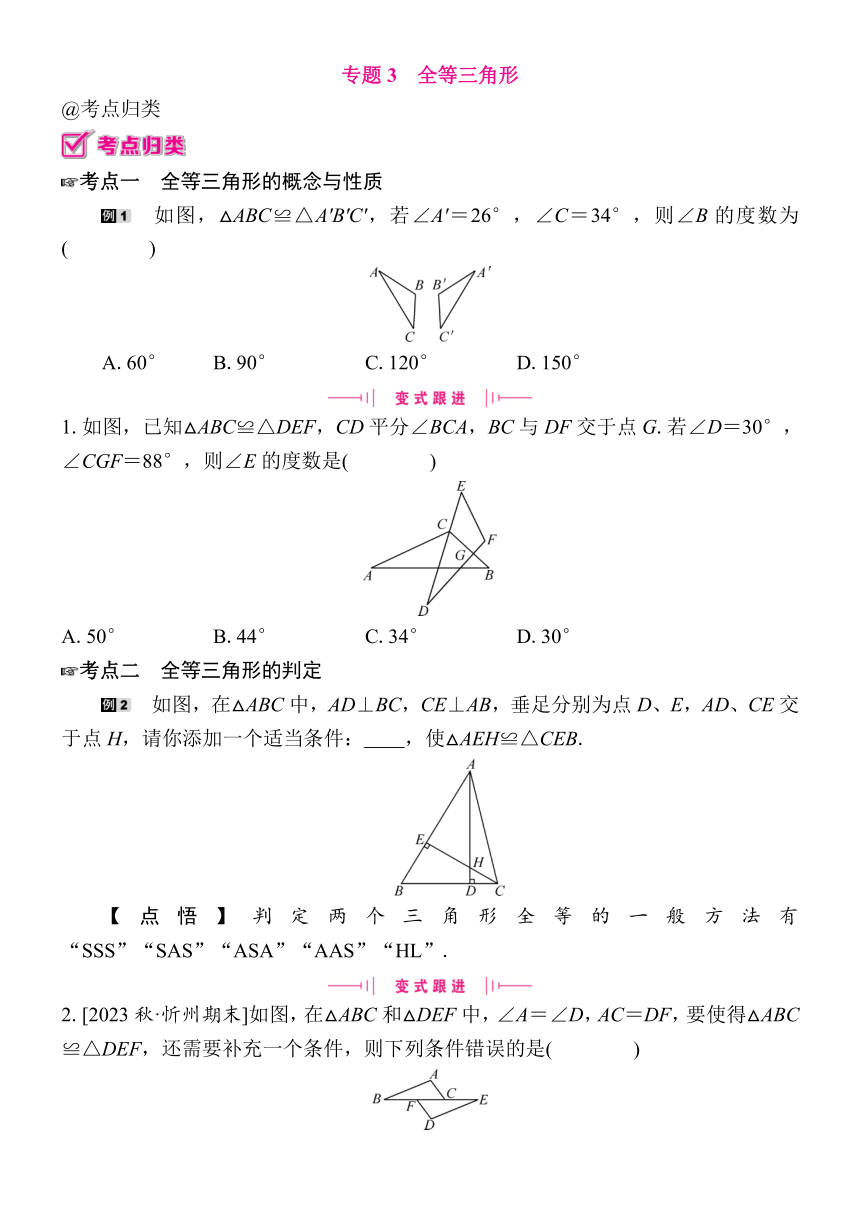 | |
| 格式 | docx | ||
| 文件大小 | 665.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 21:24:00 | ||
图片预览





文档简介
专题3 全等三角形
@考点归类
考点一 全等三角形的概念与性质
如图,△ABC≌△A'B'C',若∠A'=26°,∠C=34°,则∠B的度数为( )
A.60° B.90° C.120° D.150°
1.如图,已知△ABC≌△DEF,CD平分∠BCA,BC与DF交于点G.若∠D=30°,∠CGF=88°,则∠E的度数是( )
A.50° B.44° C.34° D.30°
考点二 全等三角形的判定
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E,AD、CE交于点H,请你添加一个适当条件: ,使△AEH≌△CEB.
【点悟】判定两个三角形全等的一般方法有“SSS”“SAS”“ASA”“AAS”“HL”.
2.[2023秋·忻州期末]如图,在△ABC和△DEF中,∠A=∠D,AC=DF,要使得△ABC≌△DEF,还需要补充一个条件,则下列条件错误的是( )
A.BF=CE B.AC∥DF
C.∠B=∠E D.AB=DE
3.[2024秋·武乡县期中]如图,在△ABC和△EBD中,BD=BC,BE=CA,∠DBE=∠C=65°,DE与CA交于点F.已知∠BDE=80°,求∠CFE的度数.
考点三 全等三角形判定与性质的综合
已知△ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;
(2)∠M=∠N.
4.如图,在△ABC中,D为边BC上一点,∠1=∠2=∠3,AC=AE.求证:
(1)△ABC≌△ADE;
(2)DA平分∠BDE.
考点四 等腰三角形的性质
如图,在△ABC中,AB=AC,BD、CE分别是△ABC的边AC、AB上的高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
5.如图,在△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于点F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若F是AC的中点,求证:∠CFD=∠B.
考点五 等腰三角形的判定
[2023春·通川区期末]在△ABC中,AB=AC,点D为射线BC上的一个动点(不与点B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连结BE.
(1)如图1,若∠BAC=∠DAE=60°,则△BEF是 三角形.
(2)若∠BAC=∠DAE≠60°,
①如图2,当点D在线段BC上移动时,判断△BEF的形状并证明.
②当点D在线段BC的延长线上移动时,△BEF是什么形状?请直接写出结论并画出相应的图形.
6.如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形的个数是 .
考点六 等边三角形的性质与判定
[2024·襄汾县中学月考]如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明理由.
(2)线段BD、DE、EC三者之间有什么关系?并说明理由.
7.如图,△BAD和△BCE都是等边三角形,连结CD、AE,AE与CD交于点F,与BC交于点M,连结BF.
(1)求证:DC=AE;
(2)求∠BFE的大小;
(3)若CM=3BM,FE=22,求BF的长度.
考点七 角平分线的性质
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【点悟】角平分线上一点到角两边的距离相等;常结合三角形全等证明有关结论.
8.如图,在△ABC中,点D在边BC上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,交BA的延长线于点F,且∠AEF=50°,连结DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
考点八 线段的垂直平分线
[2024秋·临平区期中]如图,在△ABC中,AC的垂直平分线分别交BC、AC于点E、F,且AB=CE,过点A作AD⊥BC于点D.
(1)若∠BAE=44°,求∠C的度数.
(2)若AC=7cm,△ABC的周长为17cm,求DC的长.
9.如图,在△ABC中,边AB上的垂直平分线l1交BC于点D,边AC上的垂直平分线l2交BC于点E,l1与l2相交于点O,连结OB、OC.若△ADE的周长为6cm,△OBC的周长为14cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=100°,求∠DAE的度数.
考点九 与全等三角形有关的动点问题
[2024秋·牡丹江期中]如图1,在△ABC中,AB=12cm,BC=20cm,过点C作射线CD∥AB.点M从点B出发,以4cm/s的速度沿BC匀速移动;点N从点C出发,以acm/s的速度沿CD匀速移动.点M、N同时出发,当点M到达点C时,点M、N同时停止移动,连结AM、MN,设移动时间为ts.
(1)点M、N从开始移动到停止,所用时间为 s.
(2)当△ABM与△MCN全等时,求a的值.
(3)如图2,当点M、N开始移动时,点P同时从点A出发,以3cm/s的速度沿AB向点B匀速移动,到达点B后立刻以原速度沿BA返回.当点M到达点C时,点M、N、P同时停止移动.在移动的过程中,是否存在△PBM与△MCN全等的情形?若存在,直接写出t的值;若不存在,请说明理由.
10.如图1,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时点Q在线段BD上由点B向点D运动.它们运动的时间为ts.
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
@过关训练
1.[2024秋·荆州期中]如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,∠A=∠D,AB=DE,只添加一个条件,不能判定△ABC≌△DEF的是( )
A.BF=EC B.AC=DF
C.∠ACB=∠DFE D.∠B=∠E
2.[2024秋·泉州期中]如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,则下列结论:①DC=BC;②△ADF≌△ABE;③EF=BE+DF;④AE平分∠FEB.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所成的锐角为50°,底角∠B的度数为 .
4.[2024秋·大兴区校级月考]课上老师提出了这样一个问题:如图,已知AD=AE,再添加一个条件,可以证明△ADB≌△AEC.
(1)同学们认为可以添加的条件并不唯一.
同学甲添加的条件是:AB=AC,则△ADB≌△AEC的理由是 ;
同学乙添加的条件是:∠B=∠C,则△ADB≌△AEC的理由是 ;
同学丙添加的条件是:∠ADB=∠AEC,则△ADB≌△AEC的理由是 .
(2)若添加的条件是OE=OD,求证:△ADB≌△AEC.
5.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,请判断△DEF是否为等边三角形.
6.如图,甲、乙两个勘探队对A、B、C三处的地质情况进行勘测,发现三处之间的距离两两相等.甲、乙两队分别同时从A处和B处沿着AB和BC方向以相同的速度行进,经过t小时后,分别到达P、Q处,连结PC并延长,交AQ于点G.
(1)求证:△PBC≌△QCA.
(2)在甲队从B处到P处,乙队从C处到Q处的过程中,∠CGQ的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,求出∠CGQ的度数.
7.在Rt△ABC和Rt△ADE中,AB=AC,AD=AE.连结BD、CE,过点A作AH⊥CE于点H,反向延长线段AH交BD于点F.
(1)如图1,当AB=AD时,
①请直接写出BF与DF的数量关系:BF DF(填“>”“<”或“=”);
②求证:CE=2AF.
(2)如图2,当AB≠AD时,上述①②结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
【例1】 C
【变式跟进】
1.C
【例2】 AE=CE(答案不唯一)
【变式跟进】
2.A 3.∠CFE的度数是45°.
【例3】 略
【变式跟进】
4.略
【例4】 (1)略 (2)∠BOC=100°
【变式跟进】
5.(1)∠EDF=50° (2)略
【例5】 (1)等边 (2)①△BEF为等腰三角形.证明略.
②如答图,△BEF为等腰三角形.理由略.
【变式跟进】
6.5
【例6】 (1)△ODE是等边三角形.理由略.
(2)BD=DE=EC.理由略.
【变式跟进】
7.(1)略 (2)∠BFE=60° (3)BF=
【例7】 D
【变式跟进】
8.(1)∠CAD=40° (2)略 (3)S△ABE=
【例8】 (1)∠C=34° (2)DC=5cm
【变式跟进】
9.(1)BC=6cm (2)OA=4cm
(3)∠DAE=20°
【例9】 (1)5 (2)a的值为4或.
(3)t的值为2.5或.
【变式跟进】
10.(1)当t=1时,△ACP与△BPQ全等,此时PC⊥PQ.理由略.
(2)存在或使得△ACP与△BPQ全等.
【过关训练】
1.A 2.C 3.70°或20°
4.(1)SAS AAS ASA (2)略
5.(1)略 (2)∠DEF=65°
(3)∠A=∠DEF,则△DEF是等边三角形.理由略.
6.(1)略 (2)∠CGQ的大小不会发生变化.∠CGQ=120°.
7.(1)①= ②略
(2)上述①②结论仍然成立.证明略.
。
@考点归类
考点一 全等三角形的概念与性质
如图,△ABC≌△A'B'C',若∠A'=26°,∠C=34°,则∠B的度数为( )
A.60° B.90° C.120° D.150°
1.如图,已知△ABC≌△DEF,CD平分∠BCA,BC与DF交于点G.若∠D=30°,∠CGF=88°,则∠E的度数是( )
A.50° B.44° C.34° D.30°
考点二 全等三角形的判定
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D、E,AD、CE交于点H,请你添加一个适当条件: ,使△AEH≌△CEB.
【点悟】判定两个三角形全等的一般方法有“SSS”“SAS”“ASA”“AAS”“HL”.
2.[2023秋·忻州期末]如图,在△ABC和△DEF中,∠A=∠D,AC=DF,要使得△ABC≌△DEF,还需要补充一个条件,则下列条件错误的是( )
A.BF=CE B.AC∥DF
C.∠B=∠E D.AB=DE
3.[2024秋·武乡县期中]如图,在△ABC和△EBD中,BD=BC,BE=CA,∠DBE=∠C=65°,DE与CA交于点F.已知∠BDE=80°,求∠CFE的度数.
考点三 全等三角形判定与性质的综合
已知△ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;
(2)∠M=∠N.
4.如图,在△ABC中,D为边BC上一点,∠1=∠2=∠3,AC=AE.求证:
(1)△ABC≌△ADE;
(2)DA平分∠BDE.
考点四 等腰三角形的性质
如图,在△ABC中,AB=AC,BD、CE分别是△ABC的边AC、AB上的高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
5.如图,在△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于点F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若F是AC的中点,求证:∠CFD=∠B.
考点五 等腰三角形的判定
[2023春·通川区期末]在△ABC中,AB=AC,点D为射线BC上的一个动点(不与点B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连结BE.
(1)如图1,若∠BAC=∠DAE=60°,则△BEF是 三角形.
(2)若∠BAC=∠DAE≠60°,
①如图2,当点D在线段BC上移动时,判断△BEF的形状并证明.
②当点D在线段BC的延长线上移动时,△BEF是什么形状?请直接写出结论并画出相应的图形.
6.如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形的个数是 .
考点六 等边三角形的性质与判定
[2024·襄汾县中学月考]如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明理由.
(2)线段BD、DE、EC三者之间有什么关系?并说明理由.
7.如图,△BAD和△BCE都是等边三角形,连结CD、AE,AE与CD交于点F,与BC交于点M,连结BF.
(1)求证:DC=AE;
(2)求∠BFE的大小;
(3)若CM=3BM,FE=22,求BF的长度.
考点七 角平分线的性质
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【点悟】角平分线上一点到角两边的距离相等;常结合三角形全等证明有关结论.
8.如图,在△ABC中,点D在边BC上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,交BA的延长线于点F,且∠AEF=50°,连结DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
考点八 线段的垂直平分线
[2024秋·临平区期中]如图,在△ABC中,AC的垂直平分线分别交BC、AC于点E、F,且AB=CE,过点A作AD⊥BC于点D.
(1)若∠BAE=44°,求∠C的度数.
(2)若AC=7cm,△ABC的周长为17cm,求DC的长.
9.如图,在△ABC中,边AB上的垂直平分线l1交BC于点D,边AC上的垂直平分线l2交BC于点E,l1与l2相交于点O,连结OB、OC.若△ADE的周长为6cm,△OBC的周长为14cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=100°,求∠DAE的度数.
考点九 与全等三角形有关的动点问题
[2024秋·牡丹江期中]如图1,在△ABC中,AB=12cm,BC=20cm,过点C作射线CD∥AB.点M从点B出发,以4cm/s的速度沿BC匀速移动;点N从点C出发,以acm/s的速度沿CD匀速移动.点M、N同时出发,当点M到达点C时,点M、N同时停止移动,连结AM、MN,设移动时间为ts.
(1)点M、N从开始移动到停止,所用时间为 s.
(2)当△ABM与△MCN全等时,求a的值.
(3)如图2,当点M、N开始移动时,点P同时从点A出发,以3cm/s的速度沿AB向点B匀速移动,到达点B后立刻以原速度沿BA返回.当点M到达点C时,点M、N、P同时停止移动.在移动的过程中,是否存在△PBM与△MCN全等的情形?若存在,直接写出t的值;若不存在,请说明理由.
10.如图1,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时点Q在线段BD上由点B向点D运动.它们运动的时间为ts.
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
@过关训练
1.[2024秋·荆州期中]如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,∠A=∠D,AB=DE,只添加一个条件,不能判定△ABC≌△DEF的是( )
A.BF=EC B.AC=DF
C.∠ACB=∠DFE D.∠B=∠E
2.[2024秋·泉州期中]如图,在四边形ABCD中,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E、F分别是CB、CD上的点,且∠EAF=70°,则下列结论:①DC=BC;②△ADF≌△ABE;③EF=BE+DF;④AE平分∠FEB.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所成的锐角为50°,底角∠B的度数为 .
4.[2024秋·大兴区校级月考]课上老师提出了这样一个问题:如图,已知AD=AE,再添加一个条件,可以证明△ADB≌△AEC.
(1)同学们认为可以添加的条件并不唯一.
同学甲添加的条件是:AB=AC,则△ADB≌△AEC的理由是 ;
同学乙添加的条件是:∠B=∠C,则△ADB≌△AEC的理由是 ;
同学丙添加的条件是:∠ADB=∠AEC,则△ADB≌△AEC的理由是 .
(2)若添加的条件是OE=OD,求证:△ADB≌△AEC.
5.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,请判断△DEF是否为等边三角形.
6.如图,甲、乙两个勘探队对A、B、C三处的地质情况进行勘测,发现三处之间的距离两两相等.甲、乙两队分别同时从A处和B处沿着AB和BC方向以相同的速度行进,经过t小时后,分别到达P、Q处,连结PC并延长,交AQ于点G.
(1)求证:△PBC≌△QCA.
(2)在甲队从B处到P处,乙队从C处到Q处的过程中,∠CGQ的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,求出∠CGQ的度数.
7.在Rt△ABC和Rt△ADE中,AB=AC,AD=AE.连结BD、CE,过点A作AH⊥CE于点H,反向延长线段AH交BD于点F.
(1)如图1,当AB=AD时,
①请直接写出BF与DF的数量关系:BF DF(填“>”“<”或“=”);
②求证:CE=2AF.
(2)如图2,当AB≠AD时,上述①②结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
【例1】 C
【变式跟进】
1.C
【例2】 AE=CE(答案不唯一)
【变式跟进】
2.A 3.∠CFE的度数是45°.
【例3】 略
【变式跟进】
4.略
【例4】 (1)略 (2)∠BOC=100°
【变式跟进】
5.(1)∠EDF=50° (2)略
【例5】 (1)等边 (2)①△BEF为等腰三角形.证明略.
②如答图,△BEF为等腰三角形.理由略.
【变式跟进】
6.5
【例6】 (1)△ODE是等边三角形.理由略.
(2)BD=DE=EC.理由略.
【变式跟进】
7.(1)略 (2)∠BFE=60° (3)BF=
【例7】 D
【变式跟进】
8.(1)∠CAD=40° (2)略 (3)S△ABE=
【例8】 (1)∠C=34° (2)DC=5cm
【变式跟进】
9.(1)BC=6cm (2)OA=4cm
(3)∠DAE=20°
【例9】 (1)5 (2)a的值为4或.
(3)t的值为2.5或.
【变式跟进】
10.(1)当t=1时,△ACP与△BPQ全等,此时PC⊥PQ.理由略.
(2)存在或使得△ACP与△BPQ全等.
【过关训练】
1.A 2.C 3.70°或20°
4.(1)SAS AAS ASA (2)略
5.(1)略 (2)∠DEF=65°
(3)∠A=∠DEF,则△DEF是等边三角形.理由略.
6.(1)略 (2)∠CGQ的大小不会发生变化.∠CGQ=120°.
7.(1)①= ②略
(2)上述①②结论仍然成立.证明略.
。
