宁夏回族自治区银川市永宁县三沙源上游学校2025届九年级下学期中考二模数学试卷(无答案)
文档属性
| 名称 | 宁夏回族自治区银川市永宁县三沙源上游学校2025届九年级下学期中考二模数学试卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 928.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览


文档简介
永宁三沙源上游学校2024-2025学年第二学期模考(二)
初三数学试卷
班级: 姓名: 学号:
时间:120分钟 分值:120分
一、单选题
1.2025年4月24日,长征二号F火箭成功发射神舟二十号载人飞船,首次将一种拥有强大再生能力的扁形动物涡虫送上太空.据了解,涡虫是具有亿年进化史的再生生物.将数据520000000用科学记数法表示为( )
A. B. C. D.
2.数学课上,老师找了5名同学各做了一道数学计算题,其中做对的有( )
①;②;③;④⑤
A.2个 B.3个 C.4个 D.5个
3.几个大小相同的小正方体搭成的几何体的俯视图如图所示,图中小正方形中的数字表示对应位的小正方体的个数,则该几何体的主视图是( )
A. B.C.D.
4.如图,已知直线,将一块含角的直角三角尺按如图所示的方式放置,其中斜边与直线交于点.若,则的度数为( )
B.
C. D.
5.某校学生乘车去宁夏博物馆进行研学活动.若每车坐12人,则有3人不能上车;若每车坐15人,则最后一辆车少坐6人,设学生人数为x人和车辆数为y辆,依题意可列方程组( )
A. B. C. D.
6.若关于的一元二次方程没有实数根,则直线不经过的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知点、、都在反比例函数的图象上,则,,的大小关系为( )
A. B. C. D.
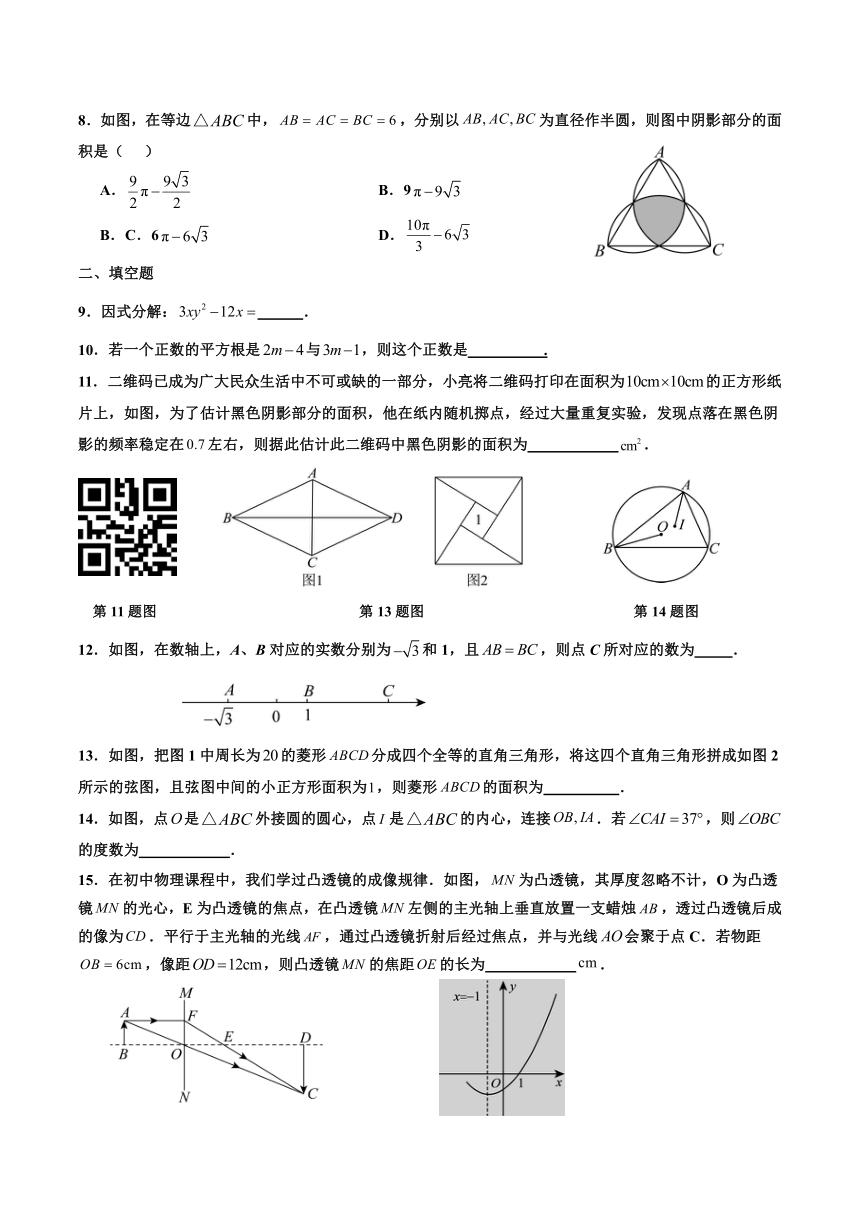
8.如图,在等边中,,分别以为直径作半圆,则图中阴影部分的面积是( )
B.9
C.6 D.
二、填空题
9.因式分解: .
10.若一个正数的平方根是与,则这个正数是 .
11.二维码已成为广大民众生活中不可或缺的一部分,小亮将二维码打印在面积为的正方形纸片上,如图,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量重复实验,发现点落在黑色阴影的频率稳定在左右,则据此估计此二维码中黑色阴影的面积为 .
第11题图 第13题图 第14题图
12.如图,在数轴上,A、B对应的实数分别为和1,且,则点C所对应的数为 .
13.如图,把图1中周长为的菱形分成四个全等的直角三角形,将这四个直角三角形拼成如图2所示的弦图,且弦图中间的小正方形面积为,则菱形的面积为 .
14.如图,点是外接圆的圆心,点是的内心,连接.若,则的度数为 .
15.在初中物理课程中,我们学过凸透镜的成像规律.如图,为凸透镜,其厚度忽略不计,O为凸透镜的光心,E为凸透镜的焦点,在凸透镜左侧的主光轴上垂直放置一支蜡烛,透过凸透镜后成的像为.平行于主光轴的光线,通过凸透镜折射后经过焦点,并与光线会聚于点C.若物距,像距,则凸透镜的焦距的长为 .
第15题图 第16题图
16.如图,二次函数图象的一部分与轴的一个交点坐标为,对称轴为直线,结合图象给出下列结论:①;②;③(为任意实数);④若点,,均在二次函数图像上,且满足,则;
其中正确的结论有 .
三、解答题
17.解不等式组
下面是某同学解不等式组的过程,请认真阅读并完成相应任务.
解:由①得: 第一步
第二步
第三步
第四步
第五步
任务一:填空:(1)以上解题过程中,第一步是依据________进行变形的.
(2)第________步开始出现错误.这一步错误的原因是________.
任务二:解不等式②,并写出该不等式组的解集.
先化简,再从0,1,2中选取一个适合的数代入求值.
19.图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上,在图①、图②、图③给定的网格中按要求画图.保留必要的作图痕迹,不要求写画法.
(1)在图①中,在线段上画出点,使.
(2)在图②中,找到一个格点,使.
(3)在图③中,在线段上画出点,使.
20.据以下素材,探索完成任务.
如何设计销售方案?
素材1 互联网时代,越来越多大山里的农产品,能够通过丰富多元的网络渠道走出大山、远销全国各地.直播助销就是运用“互联网”的一种销售方式.小明为当地特色花生与茶叶两种产品助销.已知每千克花生的售价比每千克茶叶的售价低40元.
素材2 销售50千克花生与销售10千克茶叶的总售价相同.
素材3 花生的成本为6元/千克,茶叶的成本为36元/千克,小明计划两种产品共助销60千克,总成本不高于1260元.
问题解决
任务1 假设每千克茶叶的售价为元/千克,每千克花生的售价为元/千克,请协助解决右边问题. 问题: (用含的代数式表示)
任务2 基于任务1的假设和素材2的条件,请尝试求出茶叶和花生的售价.
任务3 【拟定设计方案】请结合素材3中的信息,求出在此次助销活动中,哪种方案(分别销售花生、茶叶多少千克)可使商家获得最大利润.
21.从2009年起,每年8月8日为我国“全民健身日”,健身运动愈来愈走进人们的生活,如图是室外健身器材“漫步机”,其侧面示意图如图2所示,其中为底座,为悬臂,为路板,为横梁支杆,静正时,与地面垂直,经测量,,,,,,.(结果精确到. 参考数据:,,,,,)
(1)求点距离地面的高度;
(2)已知悬臂的长度为,可以前后摆动,当悬臂摆动至恰好与重合时,求此时踏板点距离地面的高度.
22.“生活里没有书籍,就好像没有阳光;智慧里没有书籍,就好像鸟儿没有翅膀.” 阅读对人成长的影响是巨大的.学校想了解八年级和九年级学生的阅读情况,分别从每个年级随机抽取了40名学生进行调查,收集了这80名学生一周阅读时长的数据,并对数据进行了整理、描述和分析.下面给出了部分信息.
a.八、九年级各抽取的40名学生一周阅读时长统计图如图.(统计图不完整,两个年级的数据都分成6组:,,,,,,单位:)
b.九年级学生一周阅读时长在这一组的数据为6,6,6,6,,,7,7,7,7,,.
c.八、九年级学生一周阅读时长的平均数、中位数、众数和方差如表:
年级 平均数 中位数 众数 方差
八年级 7 7
九年级 m 8
根据以上信息,回答下列问题:
(1)扇形统计图中________;
(2)补全九年级学生一周阅读时长频数分布直方图,表中m的值为________;
(3)八年级有400名学生,九年级有200名学生,请估计两个年级的学生中,一周阅读时长不低于8小时的人数;
(4)从中位数、众数、平均数、方差中,任选两个统计量,对八年级和九年级学生的阅读情况进行比较,并作出评价.
23.如图,AB为⊙O的直径,C为⊙O 上一点,连接AC,BC,过点C的直线与⊙O相切,与BA延长线交于点D,点F为CB上一点,且,,连接BF并延长交射线于点E.
(1)求证:DE⊥BE;
(2)若,DA=2,求BE的长.
24.如图,在平面直角坐标系中,直线与反比例函数在第二象限内的图象相交于点.
(1)求反比例函数的解析式;
(2)在第二象限内,根据图象直接写出的解集;
(3)将直线向上平移后与反比例函数图象在第二象限内交于点,与轴交于点,且的面积为,求直线的解析式.
25.“河畅水清、岸绿景美”,被誉为银川“城市绿脉”的典农河,正逐渐被打造成一条秀美景观带。为更好地形成“一河清水,两岸秀色,三季有花,四季常青”的生态画卷,市政养护人员安排了移动喷灌装置,移动喷灌架喷射出的水流可以近似地看成抛物线.喷灌架为一坡地草坪喷水的平面示意图,如图,喷水头的高度(喷水头距喷灌架底部的距离)是1m,当喷射出的水流与喷灌架的水平距离为10m时,水流达到最大高度6m.现将喷灌架置于坡地底部点处,草坡上距离的水平距离为15m的A处到水平地面的距离为.
(1)求该抛物线形水流的解析式;
(2)求水流的高度与斜坡铅垂高度差的最大值.
(3)若到喷水头水平距离为15m的处及其右侧种植有银杏树,由于刚在树干部分涂抹过防虫药物不能灌溉,则应将移动喷灌装置向左至少移动多少米,才能避开对银杏树的灌溉?
26.如图,中,,、外角平分线交于点,过点分别作直线,的垂线,,为垂足.
(1) °(直接写出结果不写解答过程)
(2)①求证:四边形是正方形.
②若,求的面积.
(3)如图(2),在中,,高,,则的长度是 (直接写出结果不写解答过程).
初三数学试卷
班级: 姓名: 学号:
时间:120分钟 分值:120分
一、单选题
1.2025年4月24日,长征二号F火箭成功发射神舟二十号载人飞船,首次将一种拥有强大再生能力的扁形动物涡虫送上太空.据了解,涡虫是具有亿年进化史的再生生物.将数据520000000用科学记数法表示为( )
A. B. C. D.
2.数学课上,老师找了5名同学各做了一道数学计算题,其中做对的有( )
①;②;③;④⑤
A.2个 B.3个 C.4个 D.5个
3.几个大小相同的小正方体搭成的几何体的俯视图如图所示,图中小正方形中的数字表示对应位的小正方体的个数,则该几何体的主视图是( )
A. B.C.D.
4.如图,已知直线,将一块含角的直角三角尺按如图所示的方式放置,其中斜边与直线交于点.若,则的度数为( )
B.
C. D.
5.某校学生乘车去宁夏博物馆进行研学活动.若每车坐12人,则有3人不能上车;若每车坐15人,则最后一辆车少坐6人,设学生人数为x人和车辆数为y辆,依题意可列方程组( )
A. B. C. D.
6.若关于的一元二次方程没有实数根,则直线不经过的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知点、、都在反比例函数的图象上,则,,的大小关系为( )
A. B. C. D.
8.如图,在等边中,,分别以为直径作半圆,则图中阴影部分的面积是( )
B.9
C.6 D.
二、填空题
9.因式分解: .
10.若一个正数的平方根是与,则这个正数是 .
11.二维码已成为广大民众生活中不可或缺的一部分,小亮将二维码打印在面积为的正方形纸片上,如图,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量重复实验,发现点落在黑色阴影的频率稳定在左右,则据此估计此二维码中黑色阴影的面积为 .
第11题图 第13题图 第14题图
12.如图,在数轴上,A、B对应的实数分别为和1,且,则点C所对应的数为 .
13.如图,把图1中周长为的菱形分成四个全等的直角三角形,将这四个直角三角形拼成如图2所示的弦图,且弦图中间的小正方形面积为,则菱形的面积为 .
14.如图,点是外接圆的圆心,点是的内心,连接.若,则的度数为 .
15.在初中物理课程中,我们学过凸透镜的成像规律.如图,为凸透镜,其厚度忽略不计,O为凸透镜的光心,E为凸透镜的焦点,在凸透镜左侧的主光轴上垂直放置一支蜡烛,透过凸透镜后成的像为.平行于主光轴的光线,通过凸透镜折射后经过焦点,并与光线会聚于点C.若物距,像距,则凸透镜的焦距的长为 .
第15题图 第16题图
16.如图,二次函数图象的一部分与轴的一个交点坐标为,对称轴为直线,结合图象给出下列结论:①;②;③(为任意实数);④若点,,均在二次函数图像上,且满足,则;
其中正确的结论有 .
三、解答题
17.解不等式组
下面是某同学解不等式组的过程,请认真阅读并完成相应任务.
解:由①得: 第一步
第二步
第三步
第四步
第五步
任务一:填空:(1)以上解题过程中,第一步是依据________进行变形的.
(2)第________步开始出现错误.这一步错误的原因是________.
任务二:解不等式②,并写出该不等式组的解集.
先化简,再从0,1,2中选取一个适合的数代入求值.
19.图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上,在图①、图②、图③给定的网格中按要求画图.保留必要的作图痕迹,不要求写画法.
(1)在图①中,在线段上画出点,使.
(2)在图②中,找到一个格点,使.
(3)在图③中,在线段上画出点,使.
20.据以下素材,探索完成任务.
如何设计销售方案?
素材1 互联网时代,越来越多大山里的农产品,能够通过丰富多元的网络渠道走出大山、远销全国各地.直播助销就是运用“互联网”的一种销售方式.小明为当地特色花生与茶叶两种产品助销.已知每千克花生的售价比每千克茶叶的售价低40元.
素材2 销售50千克花生与销售10千克茶叶的总售价相同.
素材3 花生的成本为6元/千克,茶叶的成本为36元/千克,小明计划两种产品共助销60千克,总成本不高于1260元.
问题解决
任务1 假设每千克茶叶的售价为元/千克,每千克花生的售价为元/千克,请协助解决右边问题. 问题: (用含的代数式表示)
任务2 基于任务1的假设和素材2的条件,请尝试求出茶叶和花生的售价.
任务3 【拟定设计方案】请结合素材3中的信息,求出在此次助销活动中,哪种方案(分别销售花生、茶叶多少千克)可使商家获得最大利润.
21.从2009年起,每年8月8日为我国“全民健身日”,健身运动愈来愈走进人们的生活,如图是室外健身器材“漫步机”,其侧面示意图如图2所示,其中为底座,为悬臂,为路板,为横梁支杆,静正时,与地面垂直,经测量,,,,,,.(结果精确到. 参考数据:,,,,,)
(1)求点距离地面的高度;
(2)已知悬臂的长度为,可以前后摆动,当悬臂摆动至恰好与重合时,求此时踏板点距离地面的高度.
22.“生活里没有书籍,就好像没有阳光;智慧里没有书籍,就好像鸟儿没有翅膀.” 阅读对人成长的影响是巨大的.学校想了解八年级和九年级学生的阅读情况,分别从每个年级随机抽取了40名学生进行调查,收集了这80名学生一周阅读时长的数据,并对数据进行了整理、描述和分析.下面给出了部分信息.
a.八、九年级各抽取的40名学生一周阅读时长统计图如图.(统计图不完整,两个年级的数据都分成6组:,,,,,,单位:)
b.九年级学生一周阅读时长在这一组的数据为6,6,6,6,,,7,7,7,7,,.
c.八、九年级学生一周阅读时长的平均数、中位数、众数和方差如表:
年级 平均数 中位数 众数 方差
八年级 7 7
九年级 m 8
根据以上信息,回答下列问题:
(1)扇形统计图中________;
(2)补全九年级学生一周阅读时长频数分布直方图,表中m的值为________;
(3)八年级有400名学生,九年级有200名学生,请估计两个年级的学生中,一周阅读时长不低于8小时的人数;
(4)从中位数、众数、平均数、方差中,任选两个统计量,对八年级和九年级学生的阅读情况进行比较,并作出评价.
23.如图,AB为⊙O的直径,C为⊙O 上一点,连接AC,BC,过点C的直线与⊙O相切,与BA延长线交于点D,点F为CB上一点,且,,连接BF并延长交射线于点E.
(1)求证:DE⊥BE;
(2)若,DA=2,求BE的长.
24.如图,在平面直角坐标系中,直线与反比例函数在第二象限内的图象相交于点.
(1)求反比例函数的解析式;
(2)在第二象限内,根据图象直接写出的解集;
(3)将直线向上平移后与反比例函数图象在第二象限内交于点,与轴交于点,且的面积为,求直线的解析式.
25.“河畅水清、岸绿景美”,被誉为银川“城市绿脉”的典农河,正逐渐被打造成一条秀美景观带。为更好地形成“一河清水,两岸秀色,三季有花,四季常青”的生态画卷,市政养护人员安排了移动喷灌装置,移动喷灌架喷射出的水流可以近似地看成抛物线.喷灌架为一坡地草坪喷水的平面示意图,如图,喷水头的高度(喷水头距喷灌架底部的距离)是1m,当喷射出的水流与喷灌架的水平距离为10m时,水流达到最大高度6m.现将喷灌架置于坡地底部点处,草坡上距离的水平距离为15m的A处到水平地面的距离为.
(1)求该抛物线形水流的解析式;
(2)求水流的高度与斜坡铅垂高度差的最大值.
(3)若到喷水头水平距离为15m的处及其右侧种植有银杏树,由于刚在树干部分涂抹过防虫药物不能灌溉,则应将移动喷灌装置向左至少移动多少米,才能避开对银杏树的灌溉?
26.如图,中,,、外角平分线交于点,过点分别作直线,的垂线,,为垂足.
(1) °(直接写出结果不写解答过程)
(2)①求证:四边形是正方形.
②若,求的面积.
(3)如图(2),在中,,高,,则的长度是 (直接写出结果不写解答过程).
同课章节目录
