2025年福建省福州市中考数学精准模拟试卷(七)(无答案)
文档属性
| 名称 | 2025年福建省福州市中考数学精准模拟试卷(七)(无答案) | 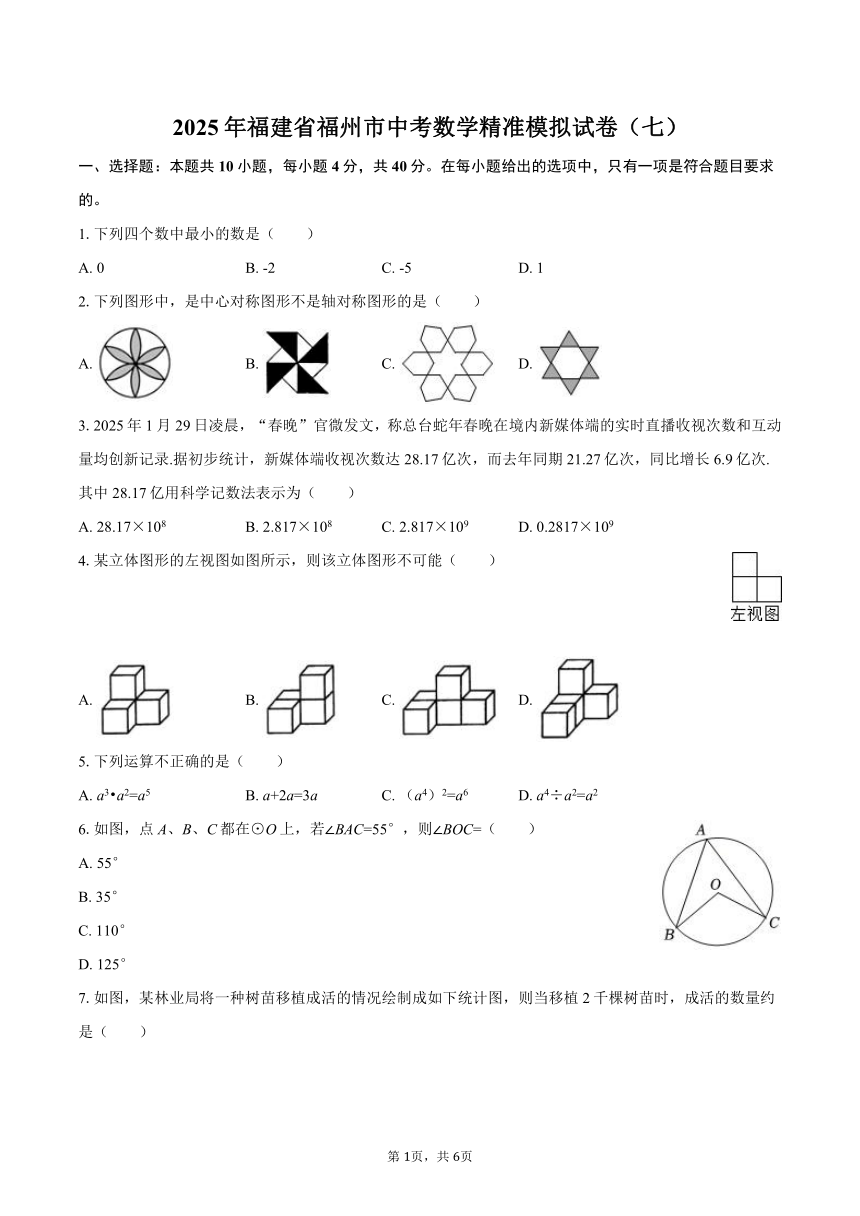 | |
| 格式 | docx | ||
| 文件大小 | 122.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 13:09:05 | ||
图片预览



文档简介
2025年福建省福州市中考数学精准模拟试卷(七)
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个数中最小的数是( )
A. 0 B. -2 C. -5 D. 1
2.下列图形中,是中心对称图形不是轴对称图形的是( )
A. B. C. D.
3.2025年1月29日凌晨,“春晚”官微发文,称总台蛇年春晚在境内新媒体端的实时直播收视次数和互动量均创新记录.据初步统计,新媒体端收视次数达28.17亿次,而去年同期21.27亿次,同比增长6.9亿次.其中28.17亿用科学记数法表示为( )
A. 28.17×108 B. 2.817×108 C. 2.817×109 D. 0.2817×109
4.某立体图形的左视图如图所示,则该立体图形不可能( )
A. B. C. D.
5.下列运算不正确的是( )
A. a3 a2=a5 B. a+2a=3a C. (a4)2=a6 D. a4÷a2=a2
6.如图,点A、B、C都在⊙O上,若∠BAC=55°,则∠BOC=( )
A. 55°
B. 35°
C. 110°
D. 125°
7.如图,某林业局将一种树苗移植成活的情况绘制成如下统计图,则当移植2千棵树苗时,成活的数量约是( )
A. 1800棵 B. 1600棵 C. 1400棵 D. 1200棵
8.若反比例函数的图象上有四点A1(-4,y1),,,A4(1,2),则y1,y2,y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y2<y1 D. y3<y1<y2
9.飞行棋是一种玩法简单的竞技游戏,玩家投掷一个骰子得到正面朝上的点数,确定前进的步数,刚好走到终点则胜利;若所得点数超过到达终点所需的步数则需要往回走所超点数的步数.如图所示,在一次飞行棋游戏的最后阶段,如果小明投掷骰子的次数不超过两次就能刚好到达终点,则到达终点的方式有( )
A. 4种 B. 5种 C. 6种 D. 7种
10.如图,在等腰三角形ABC中,AB=AC,过点C作CD⊥AB于点D,,以BD为边作正方形BDEF,点E在DC上,EF与BC交于点G.若,则EG的值为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题4分,共24分。
11.如图,直线AB,CD相交于点E,AB∥DF.若∠D=55°,则∠BEC的度数为______.
12.已知,则代数式m2-3+4n2-4mn的值为______.
13.【数学文化】我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三解,得酒五斗,问清醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒.问清、醑酒各几斗?如果设清酒x斗,那么可列方程为 .
14.如图,△ABC中,∠B=45°,AB>AC,分别以点B和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交AB于点D.若AD=2,BC=8,则AC的长为______.
15.不透明袋子中装有除颜色外形状大小均相同的5个小球,其中蓝球、红球各2个,白球1个,充分摇匀后从袋子中一次性任意取两个球,恰好为同一种颜色的概率是______.
16.在平面直角坐标系xOy中,若某动直线与抛物线的图象恒有公共点,则称该动直线为抛物线的“伴随直线”.若抛物线y=mx2+6mx+n(m>0)存在“伴随直线”y=kx+3,则n的取值范围为______.
三、解答题:本题共9小题,共86分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
如图,点E,B,C,F在一条直线上,CF=BE,AB=DC,∠ABC=∠BCD,AF与DE相交于点O.求证:∠A=∠D.
19.(本小题8分)
先化简,再求值:,其中x=1.
20.(本小题8分)
为纪念传统节日,某社团在商场购进A、B两种品牌的文化衫,已知购买A品牌文化衫花费了2500元,购买B品牌文化衫花费了2000元,且购买A品牌文化衫数量是购买B品牌文化衫数量的2倍,购买一件B品牌文化衫比购买一件A品牌文化衫多花30元.
(1)分别求A、B品牌的文化衫的单价;
(2)该社团决定再次购进与第一次购买数量相同的A、B两种品牌文化衫,同时商场对两种品牌文化衫的售价进行了调整,A品牌文化衫售价比第一次购买时提高了8%,B品牌文化衫按第一次购买时售价的9折出售,则此次购买文化衫比第一次费用高还是低?
21.(本小题8分)
如图,以△ABC的边AB为直径的⊙O交BC边于点D,交CA的延长线于点E,且∠C=∠E.
(1)求证:BD=CD.
(2)若AC=4,,求阴影部分的面积.
22.(本小题10分)
某校在进行数学测试后从两个班级中各随机抽取了10名学生按班级分成两队,整理成绩如下:(成绩得分用x表示,共分成四组:A.80≤x<85;B.85≤x<90;C.90≤x<95;D.95≤x≤100.)
甲队成绩是:96,80,96,86,99,98,92,100,91,82.
乙队成绩在C组中的数据是:94,90,92.
通过数据分析,甲队、乙队的成绩统计图表如下:
队伍 平均数 中位数 众数 方差
甲队 b c
乙队 92 93 100 50.4
根据以上信息,解答下列问题:
(1)直接写出a,b,c的值:a= ______,b= ______,c= ______;
(2)学校欲选派成绩更稳定的队伍参加市级数学竞赛,学校应选派哪一个队?请说明理由;
(3)两个班共120人参加了此次数学测试,估计两班此次数学测试成绩优秀(95≤x≤100)的学生总人数是多少?
23.(本小题10分)
阅读理解.
材料1:一个大于1的自然数,只有1和它本身两个因数的数叫质数(素数);而除了1和它本身还有别的因数的数叫合数.公元1640年,著名数学家费马发现:,,,,,而3、5、17、257、65537都是质数,于是费马猜想:对于一切自然数n,都是质数.因为运算的复杂性,很少有人去验证这个猜想.直到1732年,数学家欧拉发现:.这才说明了是合数,从而否定了费马的猜想.
材料2:一个较大的自然数是质数还是合数通常是不好直观判断的,我们可以用“N法”来判断.
主要分为三个步骤:
①找出大于N且最接近N的完全平方数k2;②用小于k的所有质数去除N;③如果这些质数都不能整除N,那么N是质数;如果这些质数中至少有一个能整除N,那么N就是合数.
(1)材料1中欧拉通过举出反例来证明费马的猜想是错误,这是证明命题错误常用的一种方法.为了证明命题“若a>b,则a2>b2”是错误的,可取的反例为______;
(2)请阅读材料2,用“N法”判断619是质数还是合数?
(3)证明存在无穷多个整数n,使n2+n+1的值是合数.
24.(本小题12分)
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0),B(3,0)两点,与y轴交于C点.
(1)2a+b= ______;
(2)点D是抛物线上一点,点E位于第四象限.若B,C,D,E四点构成的平行四边形面积为30,求E点坐标;
(3)如图2所示,过点A作两条直线分别交抛物线第一象限于点P,Q,交y轴于M,N,OM ON=n.当n为定值时,直线PQ是否必定经过某一定点?若经过,求出该定点的坐标(用含n的式子表示);若不经过,请说明理由.
25.(本小题14分)
如图,在等边△ABC中,点D为直线AC上一点,连接BD,以点B为旋转中心,将线段BD逆时针旋转120°,点D的对应点为点E,连接DE.
(1)如图1,点D在AC边上,DE交AB于点H,若∠DBC=35°,求∠ADH的度数;
(2)如图2,点D在CA延长线上,连接EC,延长AB交EC于点F,取DE的中点G,连接FG.猜想线段FG与FB,AB之间有何数量关系,并给出证明;
(3)点D在运动过程中,当线段AE的值最小时,求出的值.
第1页,共1页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个数中最小的数是( )
A. 0 B. -2 C. -5 D. 1
2.下列图形中,是中心对称图形不是轴对称图形的是( )
A. B. C. D.
3.2025年1月29日凌晨,“春晚”官微发文,称总台蛇年春晚在境内新媒体端的实时直播收视次数和互动量均创新记录.据初步统计,新媒体端收视次数达28.17亿次,而去年同期21.27亿次,同比增长6.9亿次.其中28.17亿用科学记数法表示为( )
A. 28.17×108 B. 2.817×108 C. 2.817×109 D. 0.2817×109
4.某立体图形的左视图如图所示,则该立体图形不可能( )
A. B. C. D.
5.下列运算不正确的是( )
A. a3 a2=a5 B. a+2a=3a C. (a4)2=a6 D. a4÷a2=a2
6.如图,点A、B、C都在⊙O上,若∠BAC=55°,则∠BOC=( )
A. 55°
B. 35°
C. 110°
D. 125°
7.如图,某林业局将一种树苗移植成活的情况绘制成如下统计图,则当移植2千棵树苗时,成活的数量约是( )
A. 1800棵 B. 1600棵 C. 1400棵 D. 1200棵
8.若反比例函数的图象上有四点A1(-4,y1),,,A4(1,2),则y1,y2,y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y2<y1 D. y3<y1<y2
9.飞行棋是一种玩法简单的竞技游戏,玩家投掷一个骰子得到正面朝上的点数,确定前进的步数,刚好走到终点则胜利;若所得点数超过到达终点所需的步数则需要往回走所超点数的步数.如图所示,在一次飞行棋游戏的最后阶段,如果小明投掷骰子的次数不超过两次就能刚好到达终点,则到达终点的方式有( )
A. 4种 B. 5种 C. 6种 D. 7种
10.如图,在等腰三角形ABC中,AB=AC,过点C作CD⊥AB于点D,,以BD为边作正方形BDEF,点E在DC上,EF与BC交于点G.若,则EG的值为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题4分,共24分。
11.如图,直线AB,CD相交于点E,AB∥DF.若∠D=55°,则∠BEC的度数为______.
12.已知,则代数式m2-3+4n2-4mn的值为______.
13.【数学文化】我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三解,得酒五斗,问清醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒.问清、醑酒各几斗?如果设清酒x斗,那么可列方程为 .
14.如图,△ABC中,∠B=45°,AB>AC,分别以点B和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交AB于点D.若AD=2,BC=8,则AC的长为______.
15.不透明袋子中装有除颜色外形状大小均相同的5个小球,其中蓝球、红球各2个,白球1个,充分摇匀后从袋子中一次性任意取两个球,恰好为同一种颜色的概率是______.
16.在平面直角坐标系xOy中,若某动直线与抛物线的图象恒有公共点,则称该动直线为抛物线的“伴随直线”.若抛物线y=mx2+6mx+n(m>0)存在“伴随直线”y=kx+3,则n的取值范围为______.
三、解答题:本题共9小题,共86分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
如图,点E,B,C,F在一条直线上,CF=BE,AB=DC,∠ABC=∠BCD,AF与DE相交于点O.求证:∠A=∠D.
19.(本小题8分)
先化简,再求值:,其中x=1.
20.(本小题8分)
为纪念传统节日,某社团在商场购进A、B两种品牌的文化衫,已知购买A品牌文化衫花费了2500元,购买B品牌文化衫花费了2000元,且购买A品牌文化衫数量是购买B品牌文化衫数量的2倍,购买一件B品牌文化衫比购买一件A品牌文化衫多花30元.
(1)分别求A、B品牌的文化衫的单价;
(2)该社团决定再次购进与第一次购买数量相同的A、B两种品牌文化衫,同时商场对两种品牌文化衫的售价进行了调整,A品牌文化衫售价比第一次购买时提高了8%,B品牌文化衫按第一次购买时售价的9折出售,则此次购买文化衫比第一次费用高还是低?
21.(本小题8分)
如图,以△ABC的边AB为直径的⊙O交BC边于点D,交CA的延长线于点E,且∠C=∠E.
(1)求证:BD=CD.
(2)若AC=4,,求阴影部分的面积.
22.(本小题10分)
某校在进行数学测试后从两个班级中各随机抽取了10名学生按班级分成两队,整理成绩如下:(成绩得分用x表示,共分成四组:A.80≤x<85;B.85≤x<90;C.90≤x<95;D.95≤x≤100.)
甲队成绩是:96,80,96,86,99,98,92,100,91,82.
乙队成绩在C组中的数据是:94,90,92.
通过数据分析,甲队、乙队的成绩统计图表如下:
队伍 平均数 中位数 众数 方差
甲队 b c
乙队 92 93 100 50.4
根据以上信息,解答下列问题:
(1)直接写出a,b,c的值:a= ______,b= ______,c= ______;
(2)学校欲选派成绩更稳定的队伍参加市级数学竞赛,学校应选派哪一个队?请说明理由;
(3)两个班共120人参加了此次数学测试,估计两班此次数学测试成绩优秀(95≤x≤100)的学生总人数是多少?
23.(本小题10分)
阅读理解.
材料1:一个大于1的自然数,只有1和它本身两个因数的数叫质数(素数);而除了1和它本身还有别的因数的数叫合数.公元1640年,著名数学家费马发现:,,,,,而3、5、17、257、65537都是质数,于是费马猜想:对于一切自然数n,都是质数.因为运算的复杂性,很少有人去验证这个猜想.直到1732年,数学家欧拉发现:.这才说明了是合数,从而否定了费马的猜想.
材料2:一个较大的自然数是质数还是合数通常是不好直观判断的,我们可以用“N法”来判断.
主要分为三个步骤:
①找出大于N且最接近N的完全平方数k2;②用小于k的所有质数去除N;③如果这些质数都不能整除N,那么N是质数;如果这些质数中至少有一个能整除N,那么N就是合数.
(1)材料1中欧拉通过举出反例来证明费马的猜想是错误,这是证明命题错误常用的一种方法.为了证明命题“若a>b,则a2>b2”是错误的,可取的反例为______;
(2)请阅读材料2,用“N法”判断619是质数还是合数?
(3)证明存在无穷多个整数n,使n2+n+1的值是合数.
24.(本小题12分)
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0),B(3,0)两点,与y轴交于C点.
(1)2a+b= ______;
(2)点D是抛物线上一点,点E位于第四象限.若B,C,D,E四点构成的平行四边形面积为30,求E点坐标;
(3)如图2所示,过点A作两条直线分别交抛物线第一象限于点P,Q,交y轴于M,N,OM ON=n.当n为定值时,直线PQ是否必定经过某一定点?若经过,求出该定点的坐标(用含n的式子表示);若不经过,请说明理由.
25.(本小题14分)
如图,在等边△ABC中,点D为直线AC上一点,连接BD,以点B为旋转中心,将线段BD逆时针旋转120°,点D的对应点为点E,连接DE.
(1)如图1,点D在AC边上,DE交AB于点H,若∠DBC=35°,求∠ADH的度数;
(2)如图2,点D在CA延长线上,连接EC,延长AB交EC于点F,取DE的中点G,连接FG.猜想线段FG与FB,AB之间有何数量关系,并给出证明;
(3)点D在运动过程中,当线段AE的值最小时,求出的值.
第1页,共1页
同课章节目录
