2024-2025学年江苏省镇江市丹阳市丹阳实验中学八年级(下)月考数学试卷(3月份)(无答案)
文档属性
| 名称 | 2024-2025学年江苏省镇江市丹阳市丹阳实验中学八年级(下)月考数学试卷(3月份)(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 17:50:55 | ||
图片预览



文档简介
2024-2025学年江苏省镇江市丹阳实验中学八年级(下)月考数学试卷(3月份)
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
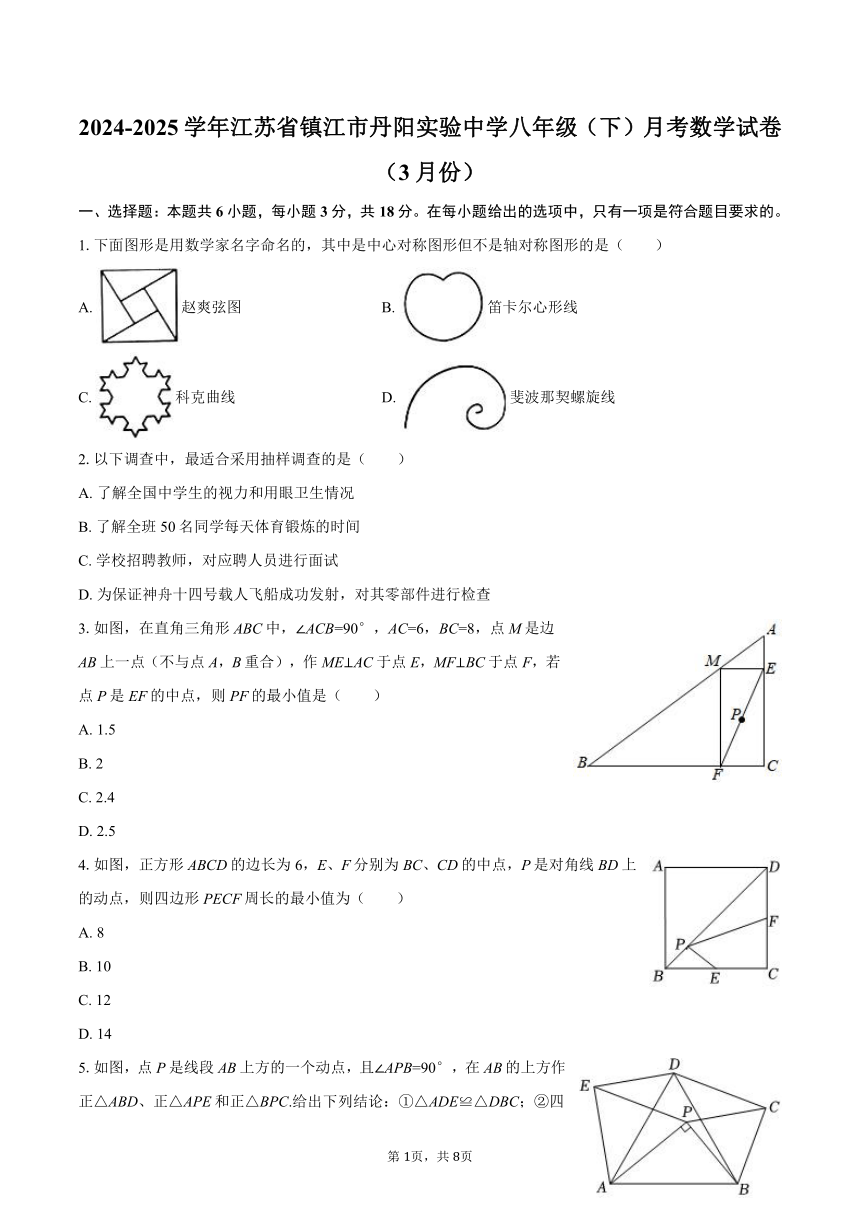
1.下面图形是用数学家名字命名的,其中是中心对称图形但不是轴对称图形的是( )
A. 赵爽弦图 B. 笛卡尔心形线
C. 科克曲线 D. 斐波那契螺旋线
2.以下调查中,最适合采用抽样调查的是( )
A. 了解全国中学生的视力和用眼卫生情况
B. 了解全班50名同学每天体育锻炼的时间
C. 学校招聘教师,对应聘人员进行面试
D. 为保证神舟十四号载人飞船成功发射,对其零部件进行检查
3.如图,在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则PF的最小值是( )
A. 1.5
B. 2
C. 2.4
D. 2.5
4.如图,正方形ABCD的边长为6,E、F分别为BC、CD的中点,P是对角线BD上的动点,则四边形PECF周长的最小值为( )
A. 8
B. 10
C. 12
D. 14
5.如图,点P是线段AB上方的一个动点,且∠APB=90°,在AB的上方作正△ABD、正△APE和正△BPC.给出下列结论:①△ADE≌△DBC;②四边形PCDE是平行四边形;③∠AED=90°;④四边形PCDE的面积大于△ABP的面积.其中正确的结论是( )
A. ①②③
B. ②③④
C. ①③④
D. ①②③④
6.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是( )
A.
B. 3+3
C. 6+
D.
二、填空题:本题共10小题,每小题3分,共30分。
7.在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频率是0.2,则第六组的频数是______.
8.小丽掷一枚质地均匀的硬币10次,有8次正面朝上,正面朝上的频率为______.
9.对于命题“若四边形ABCD中,AO=CO,BO≠DO,那么四边形ABCD不是平行四边形”.用反证法证明这个结论时,第一步应假设______.
10.在 ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为______.
11.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在线段AB上,连接BE.若BE=BD,则∠A的度数为______°.
12.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为______.(结果保留根号)
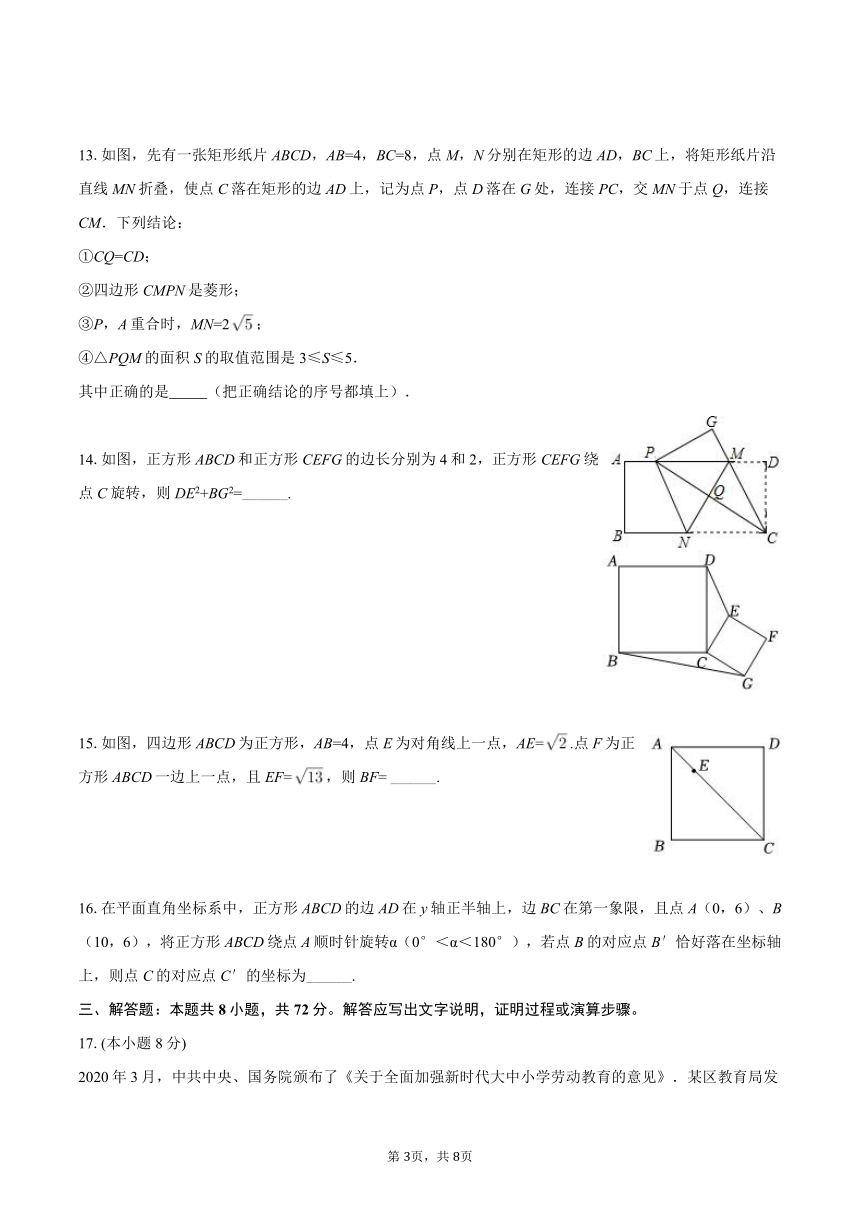
13.如图,先有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.下列结论:
①CQ=CD;
②四边形CMPN是菱形;
③P,A重合时,MN=2;
④△PQM的面积S的取值范围是3≤S≤5.
其中正确的是 (把正确结论的序号都填上).
14.如图,正方形ABCD和正方形CEFG的边长分别为4和2,正方形CEFG绕点C旋转,则DE2+BG2=______.
15.如图,四边形ABCD为正方形,AB=4,点E为对角线上一点,AE=.点F为正方形ABCD一边上一点,且EF=,则BF= ______.
16.在平面直角坐标系中,正方形ABCD的边AD在y轴正半轴上,边BC在第一象限,且点A(0,6)、B(10,6),将正方形ABCD绕点A顺时针旋转α(0°<α<180°),若点B的对应点B′恰好落在坐标轴上,则点C的对应点C′的坐标为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.某区教育局发布了“普通中小学劳动教育状况评价指标”.为了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到统计图:
(1)这次调查活动共抽取______人,“2次”所在扇形对应的圆心角是______;
(2)请将条形统计图补充完整;
(3)若该校学生共有3000人,根据调查结果,请你估计该校一周劳动“4次及以上”的学生人数.
18.(本小题8分)
某班在爱心义卖活动中设立了一个可以自由转动的转盘,如图所示,同时规定:顾客购物满20元就能获得一次转动转盘的机会,如表是活动中的统计数据:
转动转盘的次数n 100 200 300 400 500
落在“谢谢参与”区域的次数m 29 60 93 122 b
落在“谢谢参与”区域的频率 0.29 0.3 0.31 a 0.296
(1)完成上述表格:a= ,b= ;
(2)若继续不停转动转盘,当n很大时,落在“谢谢参与”区域的频率将会接近 ,假如你去转动该转盘一次,你转到“谢谢参与”的概率约是 ;(结果都精确到0.1)
(3)顾客转动转盘一次,得到奖品“盲盒”的概率记为P1,得到奖品“贴纸”的概率记为P2,得到“谢谢参与”的概率记为P3,则P1、P2、P3的大小关系是 .(用“>”连接)
19.(本小题8分)
在Rt△ABC中,∠C=90°,∠A=30°,D,E,F分别是AC,AB,BC的中点,连接ED,EF.
(1)求证:四边形DEFC是矩形;
(2)请用无刻度的直尺在图中作出∠ABC的平分线(保留作图痕迹,不写作法).
20.(本小题8分)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(1,1).
(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,画出△ABC关于原点O对称的△A2B2C2,并写出点B2的坐标______;
(3)请在x轴上找一点D得到 ACDB,则点D的坐标为______,若直线y=x+b平分 ACDB的面积,则b=______.
21.(本小题10分)
如图,在平行四边形ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F.
(1)求EF的长.
(2)把题中的条件“AD=5”去掉,其余条件不变.
①当点E与点F重合时,求AD的长.
②当点E与点C重合时,四边形ABCD的形状.
(3)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值为______.
22.(本小题8分)
我们定义:若一个凸四边形的两条对角线相等,则称这个四边形为等对角线四边形,如矩形,正方形都是等对角线四边形.
(1)如图1,已知点A,B,C在格点(小正方形的顶点)上,请在方格图中画出所有符合条件的格点D,使四边形ABCD是等对角线四边形.
(2)如图2,已知凸四边形ABCD是等对角线四边形,对角线AC,BD交于点O,点E,F分别为边AB,CD的中点,连结EF,分别与对角线BD,AC交于点M,N,若AC与BD夹角∠MON=60°.
①直接回答AC与EF的数量关系______.
②请判断△MON的形状,并说明理由?
23.(本小题10分)
如图1,将矩形ABOC放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上.若A(m,n)满足.点M是线段AC上一点,连接MO,△CMO与△NMO关于MO所在直线对称,连接AN并延长,交x轴于点P.
(1)当点P与点O重合时,在图2中用直尺和圆规作出点M(不写作法,保留作图痕迹)),并求点M的坐标;
(2)当AP∥OM时,如图3,求点P的坐标;
(3)如图4,在(2)的条件下,点D位于线段AC上,且CD=6.点E为平面内一动点,满足DE⊥OE,连PE.直接写出线段PE长度的最大值.
24.(本小题12分)
定义1:只有一组对边平行的四边形是梯形.平行的两边叫做梯形的底边,较长的一条底边叫下底,较短的一条底边叫上底,另外两边叫腰.
定义2:如果梯形的一条对角线等于上、下底之和,那么这个梯形叫和等梯形,这条对角线叫和等线.
【概念理解】
(1)如图1,在梯形ABCD中,AB∥CD,CD=4,AB=6,AD=8,AD⊥CD,四边形ABCD ______(填“是”或“不是”)和等梯形;
(2)如图2,在矩形ABCD中,AD=5,点E在AB上,AE=1,若在CD上存在点P使得四边形AEPD是和等梯形,求DP的长;
【探索发现】
(3)如图3,四边形ABCD是以AC为和等线的和等梯形,AB∥CD,AC、BD交于点O,请判别△AOB的形状,并说明理由;
【灵活运用】
(4)如图4,点E在平行四边形ABCD的边AB上,在边CD上找一点P,使得四边形AEPD是以AP为和等线的和等梯形.
要求:借助直尺和圆规用两种方法作出点P,不写作法,保留作图痕迹.
第1页,共1页
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下面图形是用数学家名字命名的,其中是中心对称图形但不是轴对称图形的是( )
A. 赵爽弦图 B. 笛卡尔心形线
C. 科克曲线 D. 斐波那契螺旋线
2.以下调查中,最适合采用抽样调查的是( )
A. 了解全国中学生的视力和用眼卫生情况
B. 了解全班50名同学每天体育锻炼的时间
C. 学校招聘教师,对应聘人员进行面试
D. 为保证神舟十四号载人飞船成功发射,对其零部件进行检查
3.如图,在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则PF的最小值是( )
A. 1.5
B. 2
C. 2.4
D. 2.5
4.如图,正方形ABCD的边长为6,E、F分别为BC、CD的中点,P是对角线BD上的动点,则四边形PECF周长的最小值为( )
A. 8
B. 10
C. 12
D. 14
5.如图,点P是线段AB上方的一个动点,且∠APB=90°,在AB的上方作正△ABD、正△APE和正△BPC.给出下列结论:①△ADE≌△DBC;②四边形PCDE是平行四边形;③∠AED=90°;④四边形PCDE的面积大于△ABP的面积.其中正确的结论是( )
A. ①②③
B. ②③④
C. ①③④
D. ①②③④
6.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是( )
A.
B. 3+3
C. 6+
D.
二、填空题:本题共10小题,每小题3分,共30分。
7.在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频率是0.2,则第六组的频数是______.
8.小丽掷一枚质地均匀的硬币10次,有8次正面朝上,正面朝上的频率为______.
9.对于命题“若四边形ABCD中,AO=CO,BO≠DO,那么四边形ABCD不是平行四边形”.用反证法证明这个结论时,第一步应假设______.
10.在 ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为______.
11.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在线段AB上,连接BE.若BE=BD,则∠A的度数为______°.
12.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为______.(结果保留根号)
13.如图,先有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.下列结论:
①CQ=CD;
②四边形CMPN是菱形;
③P,A重合时,MN=2;
④△PQM的面积S的取值范围是3≤S≤5.
其中正确的是 (把正确结论的序号都填上).
14.如图,正方形ABCD和正方形CEFG的边长分别为4和2,正方形CEFG绕点C旋转,则DE2+BG2=______.
15.如图,四边形ABCD为正方形,AB=4,点E为对角线上一点,AE=.点F为正方形ABCD一边上一点,且EF=,则BF= ______.
16.在平面直角坐标系中,正方形ABCD的边AD在y轴正半轴上,边BC在第一象限,且点A(0,6)、B(10,6),将正方形ABCD绕点A顺时针旋转α(0°<α<180°),若点B的对应点B′恰好落在坐标轴上,则点C的对应点C′的坐标为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
2020年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.某区教育局发布了“普通中小学劳动教育状况评价指标”.为了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到统计图:
(1)这次调查活动共抽取______人,“2次”所在扇形对应的圆心角是______;
(2)请将条形统计图补充完整;
(3)若该校学生共有3000人,根据调查结果,请你估计该校一周劳动“4次及以上”的学生人数.
18.(本小题8分)
某班在爱心义卖活动中设立了一个可以自由转动的转盘,如图所示,同时规定:顾客购物满20元就能获得一次转动转盘的机会,如表是活动中的统计数据:
转动转盘的次数n 100 200 300 400 500
落在“谢谢参与”区域的次数m 29 60 93 122 b
落在“谢谢参与”区域的频率 0.29 0.3 0.31 a 0.296
(1)完成上述表格:a= ,b= ;
(2)若继续不停转动转盘,当n很大时,落在“谢谢参与”区域的频率将会接近 ,假如你去转动该转盘一次,你转到“谢谢参与”的概率约是 ;(结果都精确到0.1)
(3)顾客转动转盘一次,得到奖品“盲盒”的概率记为P1,得到奖品“贴纸”的概率记为P2,得到“谢谢参与”的概率记为P3,则P1、P2、P3的大小关系是 .(用“>”连接)
19.(本小题8分)
在Rt△ABC中,∠C=90°,∠A=30°,D,E,F分别是AC,AB,BC的中点,连接ED,EF.
(1)求证:四边形DEFC是矩形;
(2)请用无刻度的直尺在图中作出∠ABC的平分线(保留作图痕迹,不写作法).
20.(本小题8分)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(1,1).
(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,画出△ABC关于原点O对称的△A2B2C2,并写出点B2的坐标______;
(3)请在x轴上找一点D得到 ACDB,则点D的坐标为______,若直线y=x+b平分 ACDB的面积,则b=______.
21.(本小题10分)
如图,在平行四边形ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F.
(1)求EF的长.
(2)把题中的条件“AD=5”去掉,其余条件不变.
①当点E与点F重合时,求AD的长.
②当点E与点C重合时,四边形ABCD的形状.
(3)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值为______.
22.(本小题8分)
我们定义:若一个凸四边形的两条对角线相等,则称这个四边形为等对角线四边形,如矩形,正方形都是等对角线四边形.
(1)如图1,已知点A,B,C在格点(小正方形的顶点)上,请在方格图中画出所有符合条件的格点D,使四边形ABCD是等对角线四边形.
(2)如图2,已知凸四边形ABCD是等对角线四边形,对角线AC,BD交于点O,点E,F分别为边AB,CD的中点,连结EF,分别与对角线BD,AC交于点M,N,若AC与BD夹角∠MON=60°.
①直接回答AC与EF的数量关系______.
②请判断△MON的形状,并说明理由?
23.(本小题10分)
如图1,将矩形ABOC放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上.若A(m,n)满足.点M是线段AC上一点,连接MO,△CMO与△NMO关于MO所在直线对称,连接AN并延长,交x轴于点P.
(1)当点P与点O重合时,在图2中用直尺和圆规作出点M(不写作法,保留作图痕迹)),并求点M的坐标;
(2)当AP∥OM时,如图3,求点P的坐标;
(3)如图4,在(2)的条件下,点D位于线段AC上,且CD=6.点E为平面内一动点,满足DE⊥OE,连PE.直接写出线段PE长度的最大值.
24.(本小题12分)
定义1:只有一组对边平行的四边形是梯形.平行的两边叫做梯形的底边,较长的一条底边叫下底,较短的一条底边叫上底,另外两边叫腰.
定义2:如果梯形的一条对角线等于上、下底之和,那么这个梯形叫和等梯形,这条对角线叫和等线.
【概念理解】
(1)如图1,在梯形ABCD中,AB∥CD,CD=4,AB=6,AD=8,AD⊥CD,四边形ABCD ______(填“是”或“不是”)和等梯形;
(2)如图2,在矩形ABCD中,AD=5,点E在AB上,AE=1,若在CD上存在点P使得四边形AEPD是和等梯形,求DP的长;
【探索发现】
(3)如图3,四边形ABCD是以AC为和等线的和等梯形,AB∥CD,AC、BD交于点O,请判别△AOB的形状,并说明理由;
【灵活运用】
(4)如图4,点E在平行四边形ABCD的边AB上,在边CD上找一点P,使得四边形AEPD是以AP为和等线的和等梯形.
要求:借助直尺和圆规用两种方法作出点P,不写作法,保留作图痕迹.
第1页,共1页
同课章节目录
