沪科版九年级数学上册23.1锐角的三角函数课件(共15张PPT)
文档属性
| 名称 | 沪科版九年级数学上册23.1锐角的三角函数课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
23.1锐角的三角函数
第23章 解直角三角形
情境导入
情境导入
怎样描述坡面的倾斜程度呢?呢?
α
坡面与水平的夹角叫做坡角(或称倾斜角),记作 α .
C1
A1
B1
100
30
C
A
B
80
30
C
A
B
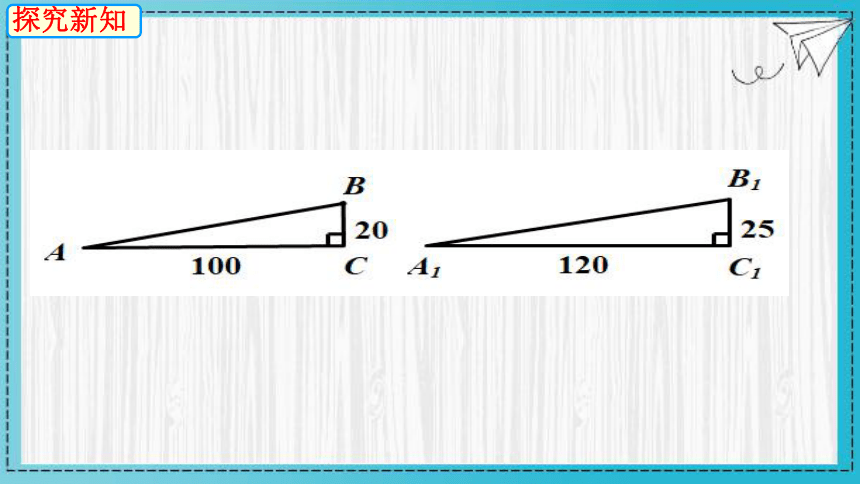
100
20
C1
A1
B1
100
30
思考:如图,坡面AB和A1B1哪个更陡?
探究新知
探究新知
在锐角A的一边上任取一点B,自点B向另一边作垂线,垂足为C,得到Rt△ABC;再任取一点B1,自点B1向另一边作垂线,垂足为C1,得到另一个Rt△AB1C1……这样,我们可以得到无数个直角三角形,这些直角三角形有什么关系?在这些直角三角形中,锐角A的对边与邻边的比值 , , ……有怎样的关系?
C1
B1
B2
C2
A
C
B
探究新知
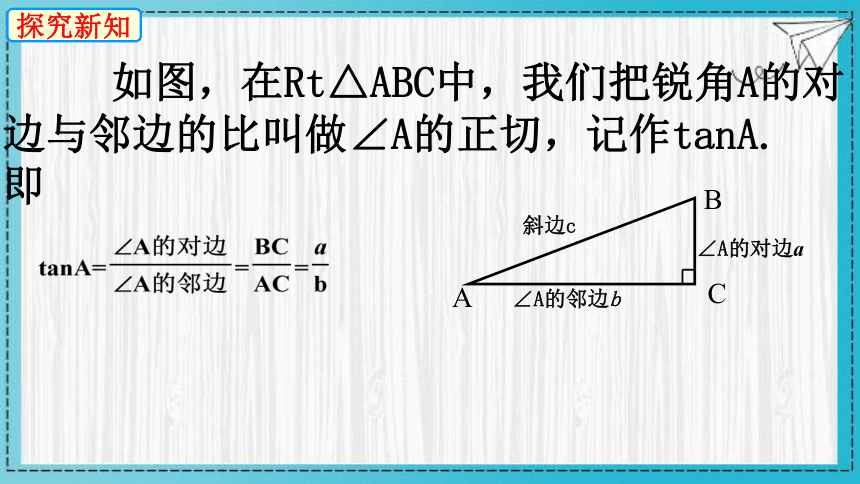
如图,在Rt△ABC中,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA.
即
C
A
B
探究新知
斜边c
∠A的对边a
∠A的邻边b
探究新知
α
探究新知
即
如图,正切经常用来描述坡面的坡度 .坡面的铅直高度 和水平长度 的比叫做坡面的坡度(或坡比),记作 .
(坡度通常写成 的形式)
坡面与水平的夹角叫做坡角
(或称倾斜角),记作α
于是有
= tanα
例1 : 如图, Rt△ABC中,∠C=90°若AC=12,BC=5.求tanA和tanB.
tanA=
tanB=
解:
=
=
C
A
B
12
5
例题讲解
2. 如图, Rt△ABC中,∠C=900 ,过点C作CD⊥AB于D.
(1) 在Rt△ACD中,tanA =_____
D
B
A
C
(2)在Rt△BCD 中,tan ∠ BCD=_____
1.如图, Rt△ABC中,∠C=90°,若AC=12,
tanA= ,则 BC=___.
C
A
B
12
5
5
12
CD
AD
BD
CD
巩固练习
( )
( )
( )
( )
=
( )
( )
巩固练习
3、如图,在Rt三角形ABC中,∠C=90°,CD⊥AB,则
CD
BD
AC
BC
AD
CD
C
A
D
B
tanB=
=
4.如图,在△ABC中,∠A=30°,tanB= , AC= ,求AB的长度
2
巩固练习
D
30°
∴ ∠A=45°
5、如图,某一水库大坝的横断面是梯形ABCD,坝顶宽CD=8m,坝高9m,迎水坡BC的坡度 =1:3,背水坡AD的坡度=1:1,求斜坡AD的坡角∠A及坝底宽AB.
E
F
解:
过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形.
∴ CD=FE=8m,CF=ED=9m
∵ 背水坡AD的坡度
=1:1
2=1:1
1=1:3
∴ DE:AE=1:1
∴ DE=AE=9cm
∵ 迎水坡BC的坡度 =1:3
∴ CF:BF=1:3
∴
BF=3CF=27(m)
∴ AB=AE+EF+CF
=9+8+27
=44(m)
答:斜坡AD的坡角∠A=45°, 坝底宽AB为44m.
本节课你有什么收获?
23.1锐角的三角函数
第23章 解直角三角形
情境导入
情境导入
怎样描述坡面的倾斜程度呢?呢?
α
坡面与水平的夹角叫做坡角(或称倾斜角),记作 α .
C1
A1
B1
100
30
C
A
B
80
30
C
A
B
100
20
C1
A1
B1
100
30
思考:如图,坡面AB和A1B1哪个更陡?
探究新知
探究新知
在锐角A的一边上任取一点B,自点B向另一边作垂线,垂足为C,得到Rt△ABC;再任取一点B1,自点B1向另一边作垂线,垂足为C1,得到另一个Rt△AB1C1……这样,我们可以得到无数个直角三角形,这些直角三角形有什么关系?在这些直角三角形中,锐角A的对边与邻边的比值 , , ……有怎样的关系?
C1
B1
B2
C2
A
C
B
探究新知
如图,在Rt△ABC中,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA.
即
C
A
B
探究新知
斜边c
∠A的对边a
∠A的邻边b
探究新知
α
探究新知
即
如图,正切经常用来描述坡面的坡度 .坡面的铅直高度 和水平长度 的比叫做坡面的坡度(或坡比),记作 .
(坡度通常写成 的形式)
坡面与水平的夹角叫做坡角
(或称倾斜角),记作α
于是有
= tanα
例1 : 如图, Rt△ABC中,∠C=90°若AC=12,BC=5.求tanA和tanB.
tanA=
tanB=
解:
=
=
C
A
B
12
5
例题讲解
2. 如图, Rt△ABC中,∠C=900 ,过点C作CD⊥AB于D.
(1) 在Rt△ACD中,tanA =_____
D
B
A
C
(2)在Rt△BCD 中,tan ∠ BCD=_____
1.如图, Rt△ABC中,∠C=90°,若AC=12,
tanA= ,则 BC=___.
C
A
B
12
5
5
12
CD
AD
BD
CD
巩固练习
( )
( )
( )
( )
=
( )
( )
巩固练习
3、如图,在Rt三角形ABC中,∠C=90°,CD⊥AB,则
CD
BD
AC
BC
AD
CD
C
A
D
B
tanB=
=
4.如图,在△ABC中,∠A=30°,tanB= , AC= ,求AB的长度
2
巩固练习
D
30°
∴ ∠A=45°
5、如图,某一水库大坝的横断面是梯形ABCD,坝顶宽CD=8m,坝高9m,迎水坡BC的坡度 =1:3,背水坡AD的坡度=1:1,求斜坡AD的坡角∠A及坝底宽AB.
E
F
解:
过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形.
∴ CD=FE=8m,CF=ED=9m
∵ 背水坡AD的坡度
=1:1
2=1:1
1=1:3
∴ DE:AE=1:1
∴ DE=AE=9cm
∵ 迎水坡BC的坡度 =1:3
∴ CF:BF=1:3
∴
BF=3CF=27(m)
∴ AB=AE+EF+CF
=9+8+27
=44(m)
答:斜坡AD的坡角∠A=45°, 坝底宽AB为44m.
本节课你有什么收获?
