北师大六年级下册《圆柱和圆锥的关系》教学设计
文档属性
| 名称 | 北师大六年级下册《圆柱和圆锥的关系》教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 446.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 18:34:05 | ||
图片预览


文档简介
圆柱和圆柱的关系教学设计
教学目标
1.能够灵活运用公式解决实际问题,熟练处理不同已知条件(半径、直径、周长、侧面积)与体积之间的转换关系;掌握等底等高、等体等底、等体等底条件下圆柱与圆锥的关联,并能利用关联解决问题。
2.通过分层练习和小组合作,提升分析问题、画图辅助解题的能力,掌握“转化已知条件”的数学思想。学会用公式推导解决复杂问题(如通过侧面积求底面周长,再求半径)。
3.在组内互助订正的过程中,培养合作学习的意识;通过严谨的公式推导和实际问题解决,体会数学的实用性,增强学习信心。
教学重难点
重点:不同已知条件下圆柱与圆锥的体积公式应用;等底等高、等体等底、等体等底条件下圆柱与圆锥的关联应用(如h锥=3h柱)。
难点:灵活转化不同已知条件;理解“等体等底时圆锥高是圆柱高的3倍”的逆向思维,避免机械套用公式导致的错误。
教学过程
智能分析、导入新课
AI前测分析,聚集本节课练习重点。
这是AI智能助手课前针对我们前测做出的分析,我们班在这块知识上相对薄弱。
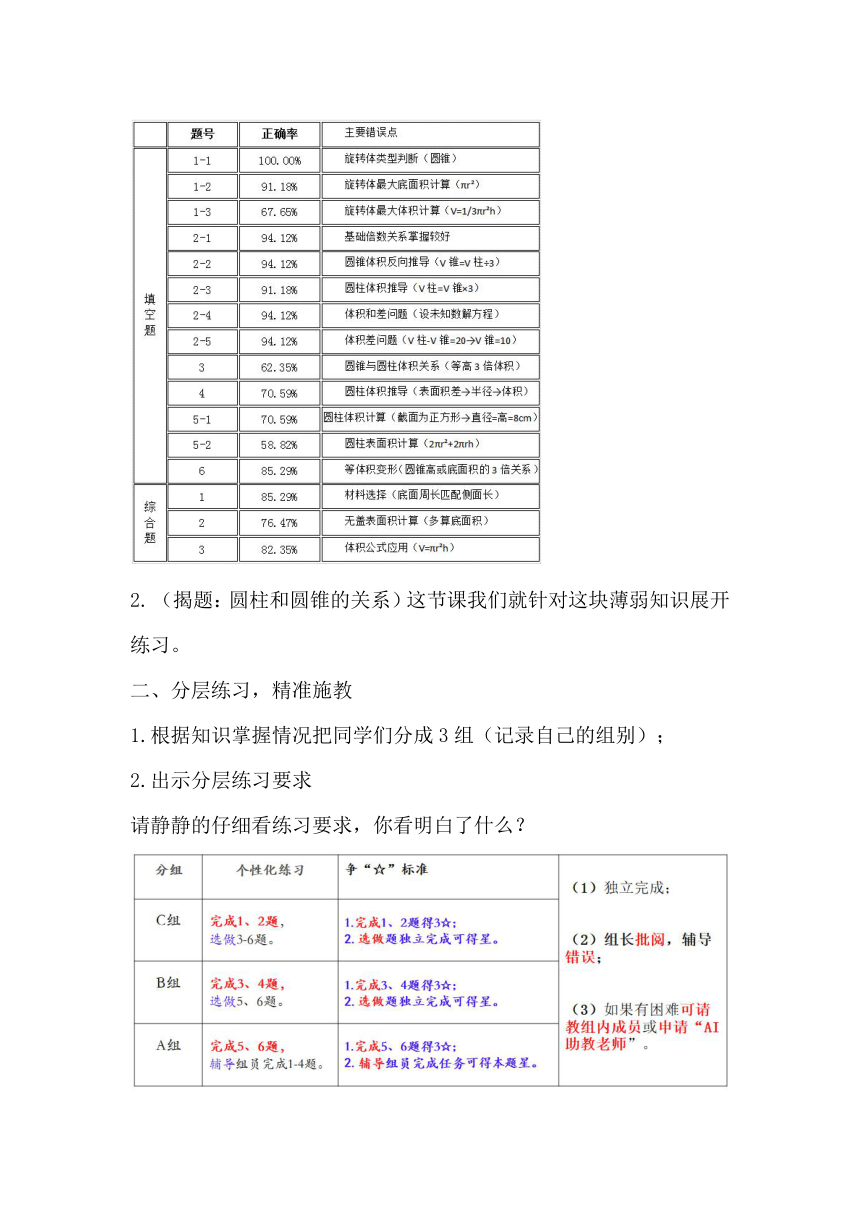
(揭题:圆柱和圆锥的关系)这节课我们就针对这块薄弱知识展开练习。
分层练习,精准施教
1.根据知识掌握情况把同学们分成3组(记录自己的组别);
2.出示分层练习要求
请静静的仔细看练习要求,你看明白了什么?
3.分层练习活动
完成组长批阅,组织组员辅导订正。
4.集体反馈
第一层面:聚焦处理不同已知条件求圆柱的体积
核对答案,得3星的举手;
对比1-5题,都是先求圆柱的体积,解题过程中有什么相同点和不同点?(同桌交流)板书圆柱和圆锥的体积计算公式,r,d,c,S侧;
小结:求圆柱的体积在已知底面积或底面半径和高时,直接利用公式计算,在已知、直径、底面周长或侧面积和高时,我们要先利用关系求出底面半径间接利用公式计算。
第二层面:解题的不同策略,感受等底等高、等体等底、等体等底条件下圆柱与圆锥的关联应用。
拍照反馈不同解法;
这3题,在求圆锥的体积、高、底面积分解法上有些不同,你能看得懂吗?(指名说)板书:等底等高、等体等底、等体等高,对应图片。
(2)小结:等底等高、等体等底或等体等底条件下,利用圆柱与圆锥的关联解题更加便捷。
根据分层练习情况,请组长给组员们打分。
三、前测纠错,举手统计纠错情况。
四、提升练习
集体反馈:本组题做对的的举手
第一题:反馈两种不同的解题方法,用第二中的举手
第2题,反馈小妙招,画图分析。
第3题,第4题,你们能看懂吗?请他来说一说。
2.学有所得评价
四、课堂行为、学习习惯评价
六、课堂总结
这节课你学到了什么?你学会了哪些解题小妙招。
板书设计
教学目标
1.能够灵活运用公式解决实际问题,熟练处理不同已知条件(半径、直径、周长、侧面积)与体积之间的转换关系;掌握等底等高、等体等底、等体等底条件下圆柱与圆锥的关联,并能利用关联解决问题。
2.通过分层练习和小组合作,提升分析问题、画图辅助解题的能力,掌握“转化已知条件”的数学思想。学会用公式推导解决复杂问题(如通过侧面积求底面周长,再求半径)。
3.在组内互助订正的过程中,培养合作学习的意识;通过严谨的公式推导和实际问题解决,体会数学的实用性,增强学习信心。
教学重难点
重点:不同已知条件下圆柱与圆锥的体积公式应用;等底等高、等体等底、等体等底条件下圆柱与圆锥的关联应用(如h锥=3h柱)。
难点:灵活转化不同已知条件;理解“等体等底时圆锥高是圆柱高的3倍”的逆向思维,避免机械套用公式导致的错误。
教学过程
智能分析、导入新课
AI前测分析,聚集本节课练习重点。
这是AI智能助手课前针对我们前测做出的分析,我们班在这块知识上相对薄弱。
(揭题:圆柱和圆锥的关系)这节课我们就针对这块薄弱知识展开练习。
分层练习,精准施教
1.根据知识掌握情况把同学们分成3组(记录自己的组别);
2.出示分层练习要求
请静静的仔细看练习要求,你看明白了什么?
3.分层练习活动
完成组长批阅,组织组员辅导订正。
4.集体反馈
第一层面:聚焦处理不同已知条件求圆柱的体积
核对答案,得3星的举手;
对比1-5题,都是先求圆柱的体积,解题过程中有什么相同点和不同点?(同桌交流)板书圆柱和圆锥的体积计算公式,r,d,c,S侧;
小结:求圆柱的体积在已知底面积或底面半径和高时,直接利用公式计算,在已知、直径、底面周长或侧面积和高时,我们要先利用关系求出底面半径间接利用公式计算。
第二层面:解题的不同策略,感受等底等高、等体等底、等体等底条件下圆柱与圆锥的关联应用。
拍照反馈不同解法;
这3题,在求圆锥的体积、高、底面积分解法上有些不同,你能看得懂吗?(指名说)板书:等底等高、等体等底、等体等高,对应图片。
(2)小结:等底等高、等体等底或等体等底条件下,利用圆柱与圆锥的关联解题更加便捷。
根据分层练习情况,请组长给组员们打分。
三、前测纠错,举手统计纠错情况。
四、提升练习
集体反馈:本组题做对的的举手
第一题:反馈两种不同的解题方法,用第二中的举手
第2题,反馈小妙招,画图分析。
第3题,第4题,你们能看懂吗?请他来说一说。
2.学有所得评价
四、课堂行为、学习习惯评价
六、课堂总结
这节课你学到了什么?你学会了哪些解题小妙招。
板书设计
