2.1.2代数式 教学设计(表格式)七年级上册(2024) 沪科版
文档属性
| 名称 | 2.1.2代数式 教学设计(表格式)七年级上册(2024) 沪科版 |
|
|
| 格式 | docx | ||
| 文件大小 | 32.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览


文档简介
课 题 《2.1.2代数式》
学科 (版本) 数学 (上海科学技术出版社) 章 节 第2章 第1节
学 时 1 年 级 七年级
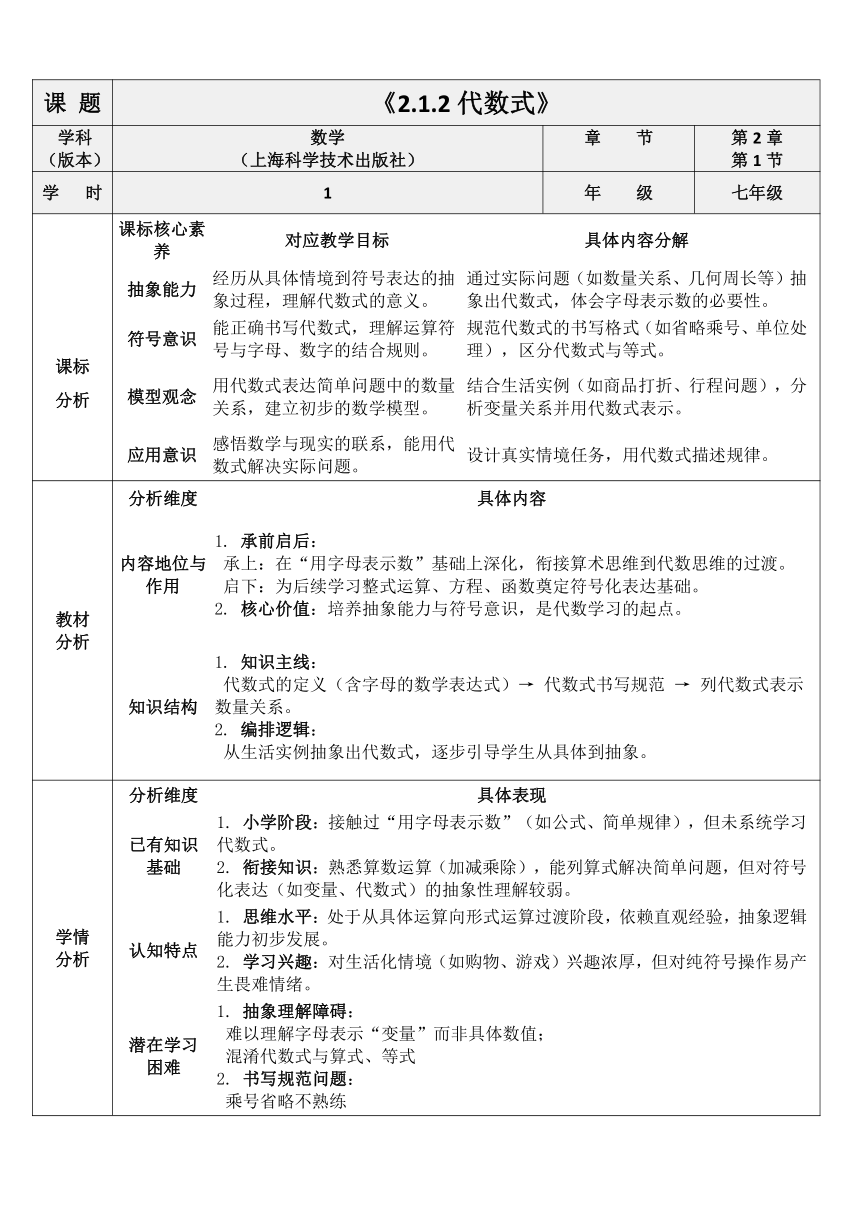
课标 分析 课标核心素养对应教学目标具体内容分解抽象能力经历从具体情境到符号表达的抽象过程,理解代数式的意义。通过实际问题(如数量关系、几何周长等)抽象出代数式,体会字母表示数的必要性。符号意识能正确书写代数式,理解运算符号与字母、数字的结合规则。规范代数式的书写格式(如省略乘号、单位处理),区分代数式与等式。模型观念用代数式表达简单问题中的数量关系,建立初步的数学模型。结合生活实例(如商品打折、行程问题),分析变量关系并用代数式表示。应用意识感悟数学与现实的联系,能用代数式解决实际问题。设计真实情境任务,用代数式描述规律。
教材 分析 分析维度具体内容内容地位与作用1. 承前启后: 承上:在“用字母表示数”基础上深化,衔接算术思维到代数思维的过渡。 启下:为后续学习整式运算、方程、函数奠定符号化表达基础。 2. 核心价值:培养抽象能力与符号意识,是代数学习的起点。知识结构1. 知识主线: 代数式的定义(含字母的数学表达式)→ 代数式书写规范 → 列代数式表示数量关系。 2. 编排逻辑: 从生活实例抽象出代数式,逐步引导学生从具体到抽象。
学情 分析 分析维度具体表现已有知识 基础1. 小学阶段:接触过“用字母表示数”(如公式、简单规律),但未系统学习代数式。 2. 衔接知识:熟悉算数运算(加减乘除),能列算式解决简单问题,但对符号化表达(如变量、代数式)的抽象性理解较弱。认知特点1. 思维水平:处于从具体运算向形式运算过渡阶段,依赖直观经验,抽象逻辑能力初步发展。 2. 学习兴趣:对生活化情境(如购物、游戏)兴趣浓厚,但对纯符号操作易产生畏难情绪。潜在学习 困难1. 抽象理解障碍: 难以理解字母表示“变量”而非具体数值; 混淆代数式与算式、等式 2. 书写规范问题: 乘号省略不熟练 除法忘变分数形式。
教学 目标 1.能正确书写代数式,理解运算符号与字母、数字的结合规则;2.用代数式表达简单问题中的数量关系,建立初步的数学模型。 3.经历从具体情境到符号表达的抽象过程,理解代数式的意义;感悟数学与现实的联系,能用代数式解决实际问题。
教学重、难点 重点1. 代数式的定义与书写规范。 2. 用代数式表示简单实际问题中的数量关系。 难点1. 从复杂情境中提取变量关系并转化为代数式; 2. 理解字母表示变量的抽象性。
教学 准备 准备类别具体内容与实施说明教师知识 准备1. 深入研读教材: 梳理代数式的定义、书写规范、列代数式的步骤及典型例题 明确代数式与算式、等式的区别。 2. 课标对标: 结合2022版课标要求,明确核心素养目标(抽象能力、符号意识、模型观念)。教具与技术准备1. 动态课件: 制作PPT动画课件展示 2. 实物教具: 准备商品价格标签、图形卡片等教具用于情境模拟。分层学习资源1. 基础层: 简单代数式书写练习 2. 提高层: 多变量代数式应用 3. 挑战层: 复杂情境建模。
教学 过程 教学内容 设计意图
活动一: 创设 情境, 导入 新课 展示课件,要求学生完成下面题目. (1)香蕉每千克售价3元,m千克售价______ 元; (2)温度由5°C上升t°C后是 °C; (3)每台电脑售价x元,降价10%后每台售价为 元; (4)某人完成一项工程需要a天,此人工作效率为 . 前面学习了用字母表示数,这节课我们就来学习代数式及其意义. 教师板书课题: 2.1.2代数式 通过复习用字母表示数或数量关系的知识,初步让学生感知代数式,为接下来学习代数式的知识奠定基础. 通过复习旧知识,使学生的知识体系更加完整,使新知识的形成水到渠成.
活动二:实践 探究, 学习 新知 1.甲、乙两地相距s km,一辆汽车以v km/h的平均速度从甲地到乙地,走完全程共需要 h. 2.圆锥的底面半径为r cm,高为h cm,它的体积为 cm . 3.把a g盐放入b g水中,完全融化后得到的盐水含盐的百分率为 . 4.正方体的所有棱长之和为12a,则它的体积为 cm . 【师生活动】学生解答,教师引导指正;2h;;a3; 【归纳总结】在前面我们还得到了41 472n,2k,2k1,k+7,a+c等,像这样用加、减、乘、除及乘方等运算符号把数或者表示数的字母连接而成的式子,叫作代数式.单个的数或字母也是代数式. 【注 意】(1)如果出现乘号,可以写成“·”或不写.数字与字母相乘时,数字写在字母前,如41 472×n写成41 472n.字母与字母相乘时,相同字母写成幂的形式,如a·a=a2.数字与数字相乘时,乘号“×”不能省略.(2)如果式中出现除法,如s÷v,一般写成 的形式. 让学生经历代数式概念产生的过程,使学生在数学活动过程中建构自己的数学知识,获得对概念的理解,发展数学能力.
活动三:例题 解析 例1 用代数式表示: (1)某商店上月收入x元,本月收入比上月的2倍还多5万元,该商店本月收入为 元; (2)一件a元的衬衫,降价10%后,价格为 元. 例题设计意图核心能力培养例11. 实际情境建模:通过商业场景(收入、价格)引导学生将现实问题转化为代数式。 2. 规范书写:强调代数式中倍数、百分比的处理(如“2倍”“降价10%”)。 从具体到抽象的转换能力 代数式书写规则的应用(如数字与字母的顺序、百分比表达)。
解:(1)2x+50 000.(2)(110%)a. 例2 用代数式表示: (1)把a本书分给若干名学生,若每人5本,还剩余3本,求学生数; (2)某次高铁列车先以290 km/h的速度运行a h,后以310 km/h的速度运行b h.求它行驶的路程. 解: (1)因为从a本书中去掉3本后,按每人5本正好分完,所以学生数为. (2)该次高铁列车行驶的路程为(290a+310b)km. 例题设计意图核心能力培养例21. 复杂关系分解:训练学生处理含余数分配(分书剩余3本)和多阶段计算(不同速度的路程)。 2. 多变量整合:引入时间、速度等变量,综合加减乘除运算。 实际问题拆解与整合能力 多变量代数式构建能力。
例3 说出下列代数式的意义: 如果圆珠笔每支售价a元,练习簿每本售价b元,那么3a+4b表示什么? 如果长方形的长、宽分别为a,b,那么(a+1)b表示什么? 解:(1)3支圆珠笔与4本练习簿的总金额. (2)长为a+1、宽为b的长方形的面积. 例题设计意图核心能力培养例31. 逆向思维训练:从代数式反推实际意义,强化符号语言与生活语言的互译能力。 2. 代数式意义理解:避免机械套用,深化数学表达的本质认知。 代数式解释与应用能力 数学语言的逻辑表达能力。
通过例题讲解,巩固所学内容.
活动四:随堂 检测 考点1 代数式的概念及书写规则 例1 下列式子a+b,S=ab,5,m,8+y,m+3=2,≥中,代数式有( ) A. 6个 B. 5个 C. 4个 D. 3个 答案:C 变式训练1 下列各式中,符合代数式书写规则的是 ( ) A. x×5 B.xy C. 2xy D. x1÷y 答案:B 考点2 列代数式 例2 “比a的3倍大5的数”用代数式表示为 ( ) A. 3a5 B. 3(a5) C. 3a+5 D. 3(a+5) 答案:C 变式训练2 一个三位数,百位数字是a,十位数字是b,个位数字是c,则这个三位数是 ( ) A. abc B. 100a+10b+c C. a+b+c D. 100c+10b+a 答案:B 考点3 代数式的意义 例3 结合实际生活说出代数式(a+0.3a)表示含义 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏.
活动五: 课堂 小结, 自我 完善 核心知识点回顾 1.代数式的定义 2.代数式的书写规范 3.列代数式的方法 4.代数式的意义 二、总结提升 1.数学思想:符号化思想 2.核心素养:抽象能力、符号意识、应用意识 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
作业 布置 基础练习:课本P87 复习题 A组 第1、2题 生活应用:记录家庭一周用电量,用代数式表示电费(如 0.5x 元,x 为用电量) 拓展思考:设计一个用代数式描述的运动计分规则(如篮球得分:2m+3n,m 为 2 分球数个数,n 为 3 分球数个数)。
板书 设计 2.1.2 代数式 1. 定义:用运算符号连接数与字母的式子 2. 书写规则: ① 数字在前,乘号省略 ② 字母相乘按顺序,幂形式 ③ 除法写成分数 3. 列代数式:找变量→定关系→写式子 4. 意义:数学语言 生活语言 提纲掣领,重点突出.
学科 (版本) 数学 (上海科学技术出版社) 章 节 第2章 第1节
学 时 1 年 级 七年级
课标 分析 课标核心素养对应教学目标具体内容分解抽象能力经历从具体情境到符号表达的抽象过程,理解代数式的意义。通过实际问题(如数量关系、几何周长等)抽象出代数式,体会字母表示数的必要性。符号意识能正确书写代数式,理解运算符号与字母、数字的结合规则。规范代数式的书写格式(如省略乘号、单位处理),区分代数式与等式。模型观念用代数式表达简单问题中的数量关系,建立初步的数学模型。结合生活实例(如商品打折、行程问题),分析变量关系并用代数式表示。应用意识感悟数学与现实的联系,能用代数式解决实际问题。设计真实情境任务,用代数式描述规律。
教材 分析 分析维度具体内容内容地位与作用1. 承前启后: 承上:在“用字母表示数”基础上深化,衔接算术思维到代数思维的过渡。 启下:为后续学习整式运算、方程、函数奠定符号化表达基础。 2. 核心价值:培养抽象能力与符号意识,是代数学习的起点。知识结构1. 知识主线: 代数式的定义(含字母的数学表达式)→ 代数式书写规范 → 列代数式表示数量关系。 2. 编排逻辑: 从生活实例抽象出代数式,逐步引导学生从具体到抽象。
学情 分析 分析维度具体表现已有知识 基础1. 小学阶段:接触过“用字母表示数”(如公式、简单规律),但未系统学习代数式。 2. 衔接知识:熟悉算数运算(加减乘除),能列算式解决简单问题,但对符号化表达(如变量、代数式)的抽象性理解较弱。认知特点1. 思维水平:处于从具体运算向形式运算过渡阶段,依赖直观经验,抽象逻辑能力初步发展。 2. 学习兴趣:对生活化情境(如购物、游戏)兴趣浓厚,但对纯符号操作易产生畏难情绪。潜在学习 困难1. 抽象理解障碍: 难以理解字母表示“变量”而非具体数值; 混淆代数式与算式、等式 2. 书写规范问题: 乘号省略不熟练 除法忘变分数形式。
教学 目标 1.能正确书写代数式,理解运算符号与字母、数字的结合规则;2.用代数式表达简单问题中的数量关系,建立初步的数学模型。 3.经历从具体情境到符号表达的抽象过程,理解代数式的意义;感悟数学与现实的联系,能用代数式解决实际问题。
教学重、难点 重点1. 代数式的定义与书写规范。 2. 用代数式表示简单实际问题中的数量关系。 难点1. 从复杂情境中提取变量关系并转化为代数式; 2. 理解字母表示变量的抽象性。
教学 准备 准备类别具体内容与实施说明教师知识 准备1. 深入研读教材: 梳理代数式的定义、书写规范、列代数式的步骤及典型例题 明确代数式与算式、等式的区别。 2. 课标对标: 结合2022版课标要求,明确核心素养目标(抽象能力、符号意识、模型观念)。教具与技术准备1. 动态课件: 制作PPT动画课件展示 2. 实物教具: 准备商品价格标签、图形卡片等教具用于情境模拟。分层学习资源1. 基础层: 简单代数式书写练习 2. 提高层: 多变量代数式应用 3. 挑战层: 复杂情境建模。
教学 过程 教学内容 设计意图
活动一: 创设 情境, 导入 新课 展示课件,要求学生完成下面题目. (1)香蕉每千克售价3元,m千克售价______ 元; (2)温度由5°C上升t°C后是 °C; (3)每台电脑售价x元,降价10%后每台售价为 元; (4)某人完成一项工程需要a天,此人工作效率为 . 前面学习了用字母表示数,这节课我们就来学习代数式及其意义. 教师板书课题: 2.1.2代数式 通过复习用字母表示数或数量关系的知识,初步让学生感知代数式,为接下来学习代数式的知识奠定基础. 通过复习旧知识,使学生的知识体系更加完整,使新知识的形成水到渠成.
活动二:实践 探究, 学习 新知 1.甲、乙两地相距s km,一辆汽车以v km/h的平均速度从甲地到乙地,走完全程共需要 h. 2.圆锥的底面半径为r cm,高为h cm,它的体积为 cm . 3.把a g盐放入b g水中,完全融化后得到的盐水含盐的百分率为 . 4.正方体的所有棱长之和为12a,则它的体积为 cm . 【师生活动】学生解答,教师引导指正;2h;;a3; 【归纳总结】在前面我们还得到了41 472n,2k,2k1,k+7,a+c等,像这样用加、减、乘、除及乘方等运算符号把数或者表示数的字母连接而成的式子,叫作代数式.单个的数或字母也是代数式. 【注 意】(1)如果出现乘号,可以写成“·”或不写.数字与字母相乘时,数字写在字母前,如41 472×n写成41 472n.字母与字母相乘时,相同字母写成幂的形式,如a·a=a2.数字与数字相乘时,乘号“×”不能省略.(2)如果式中出现除法,如s÷v,一般写成 的形式. 让学生经历代数式概念产生的过程,使学生在数学活动过程中建构自己的数学知识,获得对概念的理解,发展数学能力.
活动三:例题 解析 例1 用代数式表示: (1)某商店上月收入x元,本月收入比上月的2倍还多5万元,该商店本月收入为 元; (2)一件a元的衬衫,降价10%后,价格为 元. 例题设计意图核心能力培养例11. 实际情境建模:通过商业场景(收入、价格)引导学生将现实问题转化为代数式。 2. 规范书写:强调代数式中倍数、百分比的处理(如“2倍”“降价10%”)。 从具体到抽象的转换能力 代数式书写规则的应用(如数字与字母的顺序、百分比表达)。
解:(1)2x+50 000.(2)(110%)a. 例2 用代数式表示: (1)把a本书分给若干名学生,若每人5本,还剩余3本,求学生数; (2)某次高铁列车先以290 km/h的速度运行a h,后以310 km/h的速度运行b h.求它行驶的路程. 解: (1)因为从a本书中去掉3本后,按每人5本正好分完,所以学生数为. (2)该次高铁列车行驶的路程为(290a+310b)km. 例题设计意图核心能力培养例21. 复杂关系分解:训练学生处理含余数分配(分书剩余3本)和多阶段计算(不同速度的路程)。 2. 多变量整合:引入时间、速度等变量,综合加减乘除运算。 实际问题拆解与整合能力 多变量代数式构建能力。
例3 说出下列代数式的意义: 如果圆珠笔每支售价a元,练习簿每本售价b元,那么3a+4b表示什么? 如果长方形的长、宽分别为a,b,那么(a+1)b表示什么? 解:(1)3支圆珠笔与4本练习簿的总金额. (2)长为a+1、宽为b的长方形的面积. 例题设计意图核心能力培养例31. 逆向思维训练:从代数式反推实际意义,强化符号语言与生活语言的互译能力。 2. 代数式意义理解:避免机械套用,深化数学表达的本质认知。 代数式解释与应用能力 数学语言的逻辑表达能力。
通过例题讲解,巩固所学内容.
活动四:随堂 检测 考点1 代数式的概念及书写规则 例1 下列式子a+b,S=ab,5,m,8+y,m+3=2,≥中,代数式有( ) A. 6个 B. 5个 C. 4个 D. 3个 答案:C 变式训练1 下列各式中,符合代数式书写规则的是 ( ) A. x×5 B.xy C. 2xy D. x1÷y 答案:B 考点2 列代数式 例2 “比a的3倍大5的数”用代数式表示为 ( ) A. 3a5 B. 3(a5) C. 3a+5 D. 3(a+5) 答案:C 变式训练2 一个三位数,百位数字是a,十位数字是b,个位数字是c,则这个三位数是 ( ) A. abc B. 100a+10b+c C. a+b+c D. 100c+10b+a 答案:B 考点3 代数式的意义 例3 结合实际生活说出代数式(a+0.3a)表示含义 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏.
活动五: 课堂 小结, 自我 完善 核心知识点回顾 1.代数式的定义 2.代数式的书写规范 3.列代数式的方法 4.代数式的意义 二、总结提升 1.数学思想:符号化思想 2.核心素养:抽象能力、符号意识、应用意识 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
作业 布置 基础练习:课本P87 复习题 A组 第1、2题 生活应用:记录家庭一周用电量,用代数式表示电费(如 0.5x 元,x 为用电量) 拓展思考:设计一个用代数式描述的运动计分规则(如篮球得分:2m+3n,m 为 2 分球数个数,n 为 3 分球数个数)。
板书 设计 2.1.2 代数式 1. 定义:用运算符号连接数与字母的式子 2. 书写规则: ① 数字在前,乘号省略 ② 字母相乘按顺序,幂形式 ③ 除法写成分数 3. 列代数式:找变量→定关系→写式子 4. 意义:数学语言 生活语言 提纲掣领,重点突出.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
