2024-2025学年湖南省株洲市第一中学高一下学期学业质量摸底检测数学试题A(含答案)
文档属性
| 名称 | 2024-2025学年湖南省株洲市第一中学高一下学期学业质量摸底检测数学试题A(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 604.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 21:39:08 | ||
图片预览




文档简介
2024-2025学年湖南省株洲市第一中学高一下学期学业质量摸底检测数学试题A
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数(为虚数单位),则( )
A. 5 B. 3 C. D.
2.已知函数f(x)=sinx-ktanx+2(k∈R),若,则=( )
A. 5 B. 3 C. 1 D. 0
3.设是两个不同的平面,m是直线且m.“m∥”是“∥”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4.已知点(a,0)(a>0)是函数y=2(x-)的图象的一个对称中心,则a的最小值为( )
A. B. C. D.
5.已知D为的边的中点,O为上一点,且满足,设,,则( )
A. B. C. D.
6.某数学建模活动小组在开展主题为“空中不可到达两点的测距问题”的探究活动中,构建了如图所示的几何模型,该模型中均与平面垂直.现已测得可直接到达的两点间距离,用测角仪测得,且在点C处测得点M,N的仰角分别为,,则M,N两点之间的距离为( )
A. B. C. D.
7.在三棱锥中,,若三棱锥的外接球表面积为,则二面角的大小为( )
A. 或 B. 或 C. D.
8.已知的内角A,B,C的对边分别为a,b,c,满足,若P为内一点,且,则( )
A. 44 B. 49 C. 88 D. 98
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.若复数满足(其中是虚数单位),则( )
A.
B. 的实部是2
C. 的虚部是
D. 复数的共轭复数在复平面内对应的点在第一象限
10.在锐角中,,,则( )
A. B. C. D.
11.若将4张铁皮进行任意无重叠地切割,分别可以焊接成底面半径均为1,高均为2的一个密闭圆锥和一个密闭圆柱、上下底面半径分别为,高为2的一个密闭圆台及直径为2的一个球(不考虑损耗),则体积与其表面积之比最大的是( )
A. 球 B. 圆锥 C. 圆柱 D. 圆台
三、填空题:本题共3小题,每小题5分,共15分。
12.数据21,19,31,25,28,18,30的极差是 .
13.已知正三棱柱的高为2,底面边长为,则该三棱柱的外接球的体积为 .
14.如图所示,在棱长为2的正方体中,点M是AD的中点,动点P在正方体表面上移动,若平面,则P的轨迹长为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
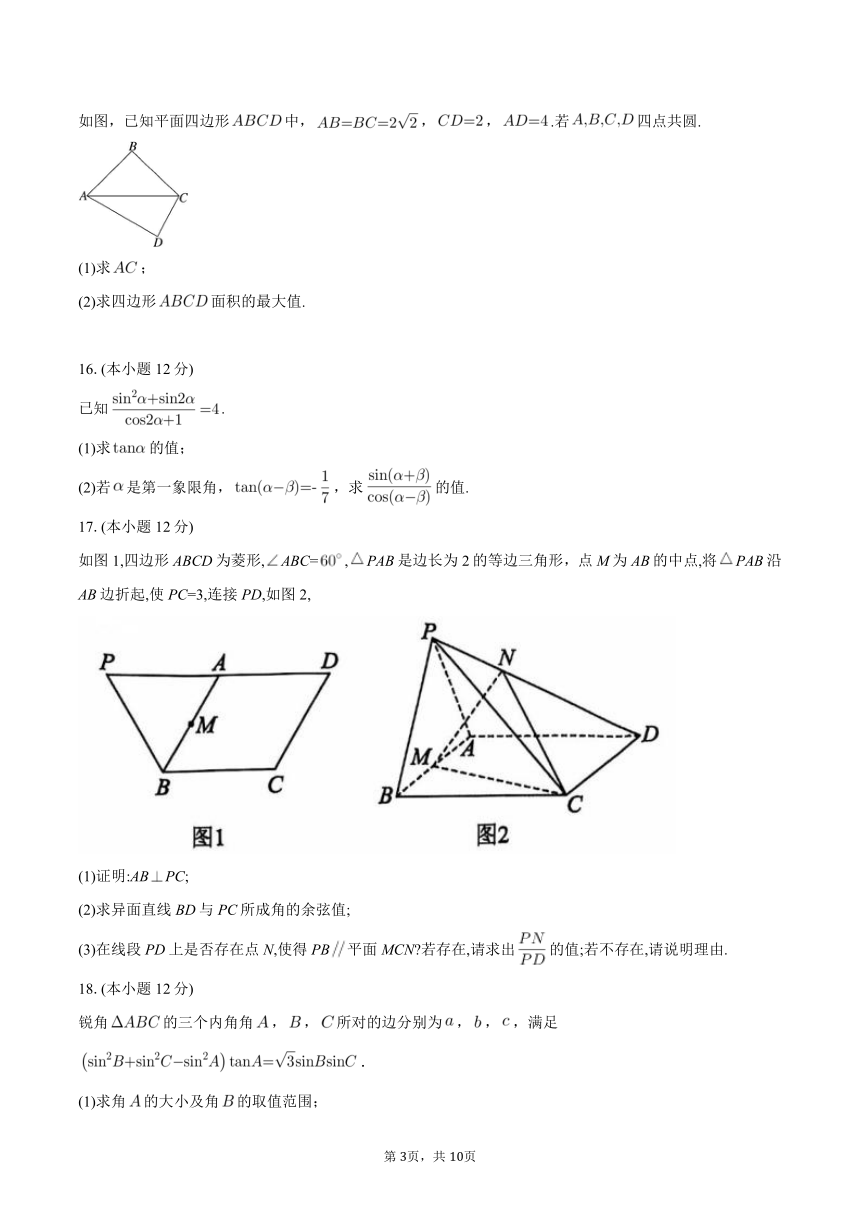
如图,已知平面四边形中,,,.若四点共圆.
(1)求;
(2)求四边形面积的最大值.
16.(本小题12分)
已知.
(1)求的值;
(2)若是第一象限角,,求的值.
17.(本小题12分)
如图1,四边形ABCD为菱形,ABC=,PAB是边长为2的等边三角形,点M为AB的中点,将PAB沿AB边折起,使PC=3,连接PD,如图2,
(1)证明:ABPC;
(2)求异面直线BD与PC所成角的余弦值;
(3)在线段PD上是否存在点N,使得PB平面MCN 若存在,请求出的值;若不存在,请说明理由.
18.(本小题12分)
锐角的三个内角角,,所对的边分别为,,,满足.
(1)求角的大小及角的取值范围;
(2)若,求的周长的取值范围;
(3)若的外接圆的圆心为,且,求的取值范围.
19.(本小题12分)
对于,记为关于的“差比模”.若取遍,记关于的“差比模”的最大值为,最小值为,若,则称关于的“差比模”是协调的.
(1)若,求关于的“差比模”;
(2)若,是否存在,使得关于的“差比模”是协调的?若存在,求出的值;若不存在,说明理由;
(3)若且,若关于的“差比模”是协调的,求的值.
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】ABD
10.【答案】ABD
11.【答案】AC
12.【答案】13
13.【答案】
14.【答案】
15.【答案】【详解】(1)在中,
在中,
因为四点共圆,所以,则,
上述两式相加得,所以(负值舍).
(2)由(1)得,化简得,
则,①
四边形的面积
,
整理得,
则,②
①②相加得,
即,
由于,当且仅当时,取得最小值,
此时四边形的面积最大,由,解得,
故四边形面积的最大值为.
16.【答案】【详解】(1)
即,解得或.
(2)由是第一象限角,由(1)可知,,又,
因为,
故.
17.【答案】解:(1)证明:连接,
∵△PAB是边长为2的等边三角形,点M为AB的中点,
∴PM⊥AB,
∵四边形ABCD为菱形,∠ABC=60°.
所以为正三角形,
∴CM⊥AB,
且PMMC=M,PM,MC平面PMC,
∴AB⊥平面PMC,
∵PC 平面PMC,
∴AB⊥PC;
(2)连接BD交MC于点E,过E作PC的平行线交PM于F点,即EF//PC,
故 为异面直线BD与PC的夹角或其补角,
由,所以点E为MC靠近点M的三等分点,
则F为PM靠近点M的三等分点,
由(1)可得为正三角形,CM⊥AB,
故,,
则,,且,
所以,,
在等腰三角形中,,
故异面直线BD与PC所成角的余弦值为;
(3)在线段PD上存在点N,使得PB平面MCN,
设点N为PD靠近点P的三等分点,连接NE,
因为点E为MC靠近点M的三等分点,
所以PB∥NE,因为NE平面MNC,PB平面MNC,
所以PB∥平面MNC,满足题意,
故线段PD上存在点N,使得PB∥平面MNC,且PN=.
18.【答案】【详解】(1)锐角的三个内角角,,所对的边分别为,,,
因为,
由正弦定理可得,
所以,
故,因为为锐角,所以,
因为为锐角三角形,则,
解得,所以,角的取值范围是.
(2)因为,由正弦定理得,
所以
因为,所以,所以,
所以,所以,
所以周长的取值范围为
(3)设的外接圆半径为,所以,
,所以
设,则,则,
所以
因为,所以,所以,所以,
所以,所以的取值范围为.
19.【答案】解:(1)由题意得:,
故关于的“差比模”为.
(2)先证明共轭复数有如下性质:若任意,则.
证明:设,
则,
而,
故;
,
,
故,
综上,共轭复数的性质得证.
记当“差比模”取最大值时的复数为,即,
由已知发现,
由已证明共轭复数的性质与复数模的性质可得,
因为,
所以若当时取得,则时取到,
故可知,
由取遍,不恒为常数,则,
故由基本不等式可得,
故不存在,使得关于的“差比模”是协调的.
(3)且,设,
则,
平方整理可得:
所以,
即,
平方整理得:,
令,设方程,
则,
故方程有两个不等的实数根,设为,不妨设,
由题意知,,
则,且,
故方程有两不等的正实数根,
由关于的不等式,
解得,则,,
由已知关于的“差比模”是协调的,则,
所以,
利用韦达定理,,
则有,
化简可得,
故.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数(为虚数单位),则( )
A. 5 B. 3 C. D.
2.已知函数f(x)=sinx-ktanx+2(k∈R),若,则=( )
A. 5 B. 3 C. 1 D. 0
3.设是两个不同的平面,m是直线且m.“m∥”是“∥”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4.已知点(a,0)(a>0)是函数y=2(x-)的图象的一个对称中心,则a的最小值为( )
A. B. C. D.
5.已知D为的边的中点,O为上一点,且满足,设,,则( )
A. B. C. D.
6.某数学建模活动小组在开展主题为“空中不可到达两点的测距问题”的探究活动中,构建了如图所示的几何模型,该模型中均与平面垂直.现已测得可直接到达的两点间距离,用测角仪测得,且在点C处测得点M,N的仰角分别为,,则M,N两点之间的距离为( )
A. B. C. D.
7.在三棱锥中,,若三棱锥的外接球表面积为,则二面角的大小为( )
A. 或 B. 或 C. D.
8.已知的内角A,B,C的对边分别为a,b,c,满足,若P为内一点,且,则( )
A. 44 B. 49 C. 88 D. 98
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.若复数满足(其中是虚数单位),则( )
A.
B. 的实部是2
C. 的虚部是
D. 复数的共轭复数在复平面内对应的点在第一象限
10.在锐角中,,,则( )
A. B. C. D.
11.若将4张铁皮进行任意无重叠地切割,分别可以焊接成底面半径均为1,高均为2的一个密闭圆锥和一个密闭圆柱、上下底面半径分别为,高为2的一个密闭圆台及直径为2的一个球(不考虑损耗),则体积与其表面积之比最大的是( )
A. 球 B. 圆锥 C. 圆柱 D. 圆台
三、填空题:本题共3小题,每小题5分,共15分。
12.数据21,19,31,25,28,18,30的极差是 .
13.已知正三棱柱的高为2,底面边长为,则该三棱柱的外接球的体积为 .
14.如图所示,在棱长为2的正方体中,点M是AD的中点,动点P在正方体表面上移动,若平面,则P的轨迹长为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
如图,已知平面四边形中,,,.若四点共圆.
(1)求;
(2)求四边形面积的最大值.
16.(本小题12分)
已知.
(1)求的值;
(2)若是第一象限角,,求的值.
17.(本小题12分)
如图1,四边形ABCD为菱形,ABC=,PAB是边长为2的等边三角形,点M为AB的中点,将PAB沿AB边折起,使PC=3,连接PD,如图2,
(1)证明:ABPC;
(2)求异面直线BD与PC所成角的余弦值;
(3)在线段PD上是否存在点N,使得PB平面MCN 若存在,请求出的值;若不存在,请说明理由.
18.(本小题12分)
锐角的三个内角角,,所对的边分别为,,,满足.
(1)求角的大小及角的取值范围;
(2)若,求的周长的取值范围;
(3)若的外接圆的圆心为,且,求的取值范围.
19.(本小题12分)
对于,记为关于的“差比模”.若取遍,记关于的“差比模”的最大值为,最小值为,若,则称关于的“差比模”是协调的.
(1)若,求关于的“差比模”;
(2)若,是否存在,使得关于的“差比模”是协调的?若存在,求出的值;若不存在,说明理由;
(3)若且,若关于的“差比模”是协调的,求的值.
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】ABD
10.【答案】ABD
11.【答案】AC
12.【答案】13
13.【答案】
14.【答案】
15.【答案】【详解】(1)在中,
在中,
因为四点共圆,所以,则,
上述两式相加得,所以(负值舍).
(2)由(1)得,化简得,
则,①
四边形的面积
,
整理得,
则,②
①②相加得,
即,
由于,当且仅当时,取得最小值,
此时四边形的面积最大,由,解得,
故四边形面积的最大值为.
16.【答案】【详解】(1)
即,解得或.
(2)由是第一象限角,由(1)可知,,又,
因为,
故.
17.【答案】解:(1)证明:连接,
∵△PAB是边长为2的等边三角形,点M为AB的中点,
∴PM⊥AB,
∵四边形ABCD为菱形,∠ABC=60°.
所以为正三角形,
∴CM⊥AB,
且PMMC=M,PM,MC平面PMC,
∴AB⊥平面PMC,
∵PC 平面PMC,
∴AB⊥PC;
(2)连接BD交MC于点E,过E作PC的平行线交PM于F点,即EF//PC,
故 为异面直线BD与PC的夹角或其补角,
由,所以点E为MC靠近点M的三等分点,
则F为PM靠近点M的三等分点,
由(1)可得为正三角形,CM⊥AB,
故,,
则,,且,
所以,,
在等腰三角形中,,
故异面直线BD与PC所成角的余弦值为;
(3)在线段PD上存在点N,使得PB平面MCN,
设点N为PD靠近点P的三等分点,连接NE,
因为点E为MC靠近点M的三等分点,
所以PB∥NE,因为NE平面MNC,PB平面MNC,
所以PB∥平面MNC,满足题意,
故线段PD上存在点N,使得PB∥平面MNC,且PN=.
18.【答案】【详解】(1)锐角的三个内角角,,所对的边分别为,,,
因为,
由正弦定理可得,
所以,
故,因为为锐角,所以,
因为为锐角三角形,则,
解得,所以,角的取值范围是.
(2)因为,由正弦定理得,
所以
因为,所以,所以,
所以,所以,
所以周长的取值范围为
(3)设的外接圆半径为,所以,
,所以
设,则,则,
所以
因为,所以,所以,所以,
所以,所以的取值范围为.
19.【答案】解:(1)由题意得:,
故关于的“差比模”为.
(2)先证明共轭复数有如下性质:若任意,则.
证明:设,
则,
而,
故;
,
,
故,
综上,共轭复数的性质得证.
记当“差比模”取最大值时的复数为,即,
由已知发现,
由已证明共轭复数的性质与复数模的性质可得,
因为,
所以若当时取得,则时取到,
故可知,
由取遍,不恒为常数,则,
故由基本不等式可得,
故不存在,使得关于的“差比模”是协调的.
(3)且,设,
则,
平方整理可得:
所以,
即,
平方整理得:,
令,设方程,
则,
故方程有两个不等的实数根,设为,不妨设,
由题意知,,
则,且,
故方程有两不等的正实数根,
由关于的不等式,
解得,则,,
由已知关于的“差比模”是协调的,则,
所以,
利用韦达定理,,
则有,
化简可得,
故.
第1页,共1页
同课章节目录
