12.2 一次函数模型的应用 教学设计(表格式) 初中数学沪科版(2024)八年级上册
文档属性
| 名称 | 12.2 一次函数模型的应用 教学设计(表格式) 初中数学沪科版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览



文档简介
沪科版八年级数学上册12章一次函数 课题: 一次函数模型的应用
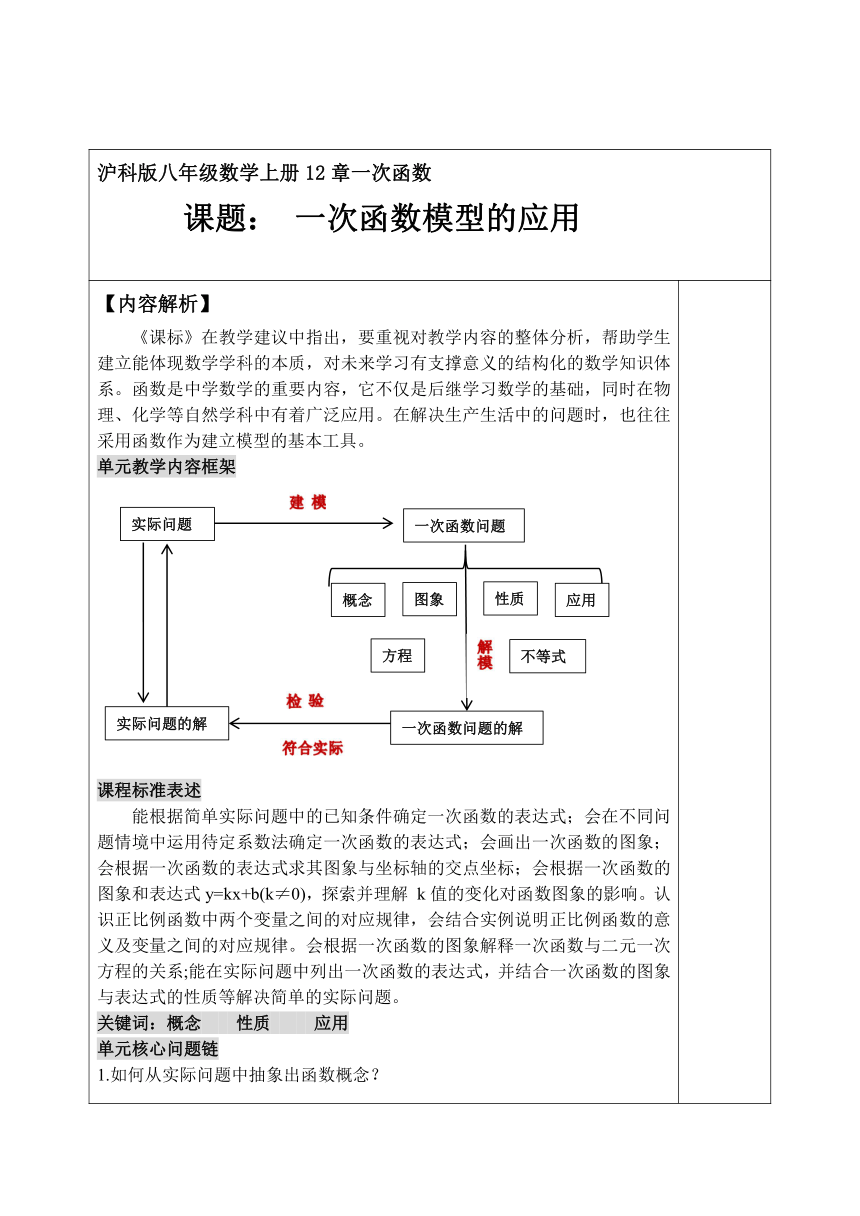
【内容解析】 《课标》在教学建议中指出,要重视对教学内容的整体分析,帮助学生建立能体现数学学科的本质,对未来学习有支撑意义的结构化的数学知识体系。函数是中学数学的重要内容,它不仅是后继学习数学的基础,同时在物理、化学等自然学科中有着广泛应用。在解决生产生活中的问题时,也往往采用函数作为建立模型的基本工具。 单元教学内容框架 课程标准表述 能根据简单实际问题中的已知条件确定一次函数的表达式;会在不同问题情境中运用待定系数法确定一次函数的表达式;会画出一次函数的图象;会根据一次函数的表达式求其图象与坐标轴的交点坐标;会根据一次函数的图象和表达式y=kx+b(k≠0),探索并理解 k值的变化对函数图象的影响。认识正比例函数中两个变量之间的对应规律,会结合实例说明正比例函数的意义及变量之间的对应规律。会根据一次函数的图象解释一次函数与二元一次方程的关系;能在实际问题中列出一次函数的表达式,并结合一次函数的图象与表达式的性质等解决简单的实际问题。 关键词:概念 性质 应用 单元核心问题链 1.如何从实际问题中抽象出函数概念? 2.如何数形结合得到一次函数的性质? 3.如何用一次函数解决问题? 【目标设置】 单元目标 1.探索实例中的数量关系和变化规律,了解常量、变量的意义。理解函数的概念和三种表示法.能确定简单问题中函数自变量的取值范围,并会求出函数值. 2.结合情境体会一次函数的意义,会利用待定系数法确定一次函数的表达式. 3.能画出一次函数图象,根据一次函数图象及表达式y=kx+b(k≠0)探索并理解k>0和k<0时,图象的变化情况. 4.体会一次函数与二元一次方程的关系. 5.能用一次函数解决简单的实际问题. 单元重难点 重点:结合实例掌握一次函数的概念,结合图像讨论性质,运用一次函数的图像和性质解决实际问题; 难点:函数概念的建立和利用一次函数的图象和性质解决简单实际问题。 课时重难点 重点:建立一次函数模型解决简单实际问题; 难点:把实际问题抽象出数学问题。 课时目标 掌握从实际问题抽象函数问题的方式方法,会借助一次函数解决实际问题 经历提出问题—分析问题—解决问题的过程,培养将实际问题抽象数学问题的能力; 在建构新知识的过程中,发展应用意识和创新意识,体会数学的应用价值 教学策略 教法:采用基于问题解决的任务驱动教学方式 学法:采用自主探究、合作交流的学习方法,让学生带着问题学,在探索中学,在动手操作中学。 【教学设计】 确定研究内容 建立函数模型 利用模型解题 根据模型拓展 确定研究内容 实践探究:学生以兴趣小组的形式去主动寻找生活中变化的内容,寻找可以借助一次函数解决的问题。 等等 为了提醒人们节约用水,及时关好水龙头,班里同学分工做了水龙头出水实验,他们用于接水的量筒的最大容量为500ml。 设计意图:一次函数是刻画变化的模型,以往的教学中教师通常直接给出情景,建立模型,解决问题。但是对于生活中的情景,把生活情景数学化是难点,为了培养学生用数学的眼光观察世界的能力,设计实践探究活动,让学生去寻找和发现生活中的变化内容。在确定研究内容的过程中,培养学生发现问题、提出问题的能力。 建立函数模型 问题1、在水龙头出水的过程中涉及哪些量? 问题2、研究哪些量之间的关系? 问题3、如何测出水速度? 学生交流讨论,做水龙头流水实验。 实验:同学在做水龙头出水实验时,每隔10s观察量筒中水的体积,记录的数据如下表(出的水量精确到1ml); 通过多次测量取平均值得到下表,并填写内容。 时间t(秒)10203040506070流出的水量V(毫升)
设计意图:让学生思想的火花充分跳跃,培养学生用数学的思维思考世界的能力,在教学中引导学生得出研究对象中的函数关系:①量筒内水的体积=出水速度×出水时间;②量筒剩余容量=量筒容量-量筒内水的体积 利用模型解题 问题4、能否把变化过程用数学表达式表示? 问题5、如何更直观的反应这个变化过程? 问题6、观察一次函数图象,你能获取哪些信息? 问题7、能否用上述模型预测一个小时没关水龙头将浪费多少水资源?对此,我们应该怎么做? 设计意图:培养学生识图能力和从图像中获取信息的能力。综合与实践是促进学生深度学习、培育数学核心素养的有效途径,它具有重要的育人价值。基于单元整体视角,将综合与实践纳入单元整体设计,是实现数学综合与时间常态化实施的有效途径。 根据模型拓展 问题8、如何将这个问题情景进行迁移?(还有哪些情景可以用这个函数图象解释呢?) 设计意图:为了让学生理解一次函数可以表示一类现实事物运动变化规律,让学生在小组交流等活动,展开充分想象去构造不同的实际情景表述这个函数关系中,加深对一次函数的认识,发展几何直观,培养学生学习数学的兴趣,感悟数学与生活的密切联系。 【作业布置】 A层基础 某养猪场欲买饲料喂猪,相关数据如下表: 饲料种类/元饲料单价元/kg猪食量kg/天猪增重kg/天A2.82.51.0B2.32.50.9
由市场行情得知,屠宰场收购生猪每千克单价在10~15元范围内. (1)设收购生猪每千克单价为x元,分别列出喂A,B两种饲料的日利润y元的 函数表达式;(日利润 =日收益-日饲料成本) (2)选用哪种饲料合算 B层提升 球从高处下落再反弹起来,可以直观地看出球的下落高度越高,反弹高度也就越高,那么球下落高度与反弹高度具有怎样的关系呢 请你进行实验,将实验数据填入下表,并根据实验数据建立球下落高度和反弹高度之间关系的函数模型. 试验次数第1次第2次第3次第4次第5次第5次下落高度/cm反弹高度/cm
拓展作业 根据水龙头中的数学,完成一篇小论文 设计意图:A层重基础,B层注重提升,同时在拓展作业中以学习小组的完成水龙头中的数学的小论文。分层作业尊重学生的思维层级和个体需求。 【板书设计】 一次函数模型的应用 【教学思考】 学生对数学具有好奇心和求知欲,了解数学的价值,欣赏数学美,提高学习数学的兴趣,建立学好数学的信心,养成良好的学习习惯,形成质疑问难,自我反思和用于探索的科学精神。本节课聚焦在实践中获得知识,并由此展开教学设计,学生亲身体验,寻找生活中的一次函数,构造真实有效的情景,让学生用数学的眼光观察世界;学生观察数轴,看横轴看纵轴,看函数图象的变化趋势,经历学数学、用数学的过程,培养学生会数学的思维思考世界,用数学的思维表达世界,培养学生的核心素养;通过对一次函数构造不同的情景,抓住一次函数是两个变量之间的关系的本质,强化学生对函数模型的认识。 课堂观察检测表 学生姓名: 年级 : 观察时间: 年 月 日 因素ABC说明1.能否小组合作找的到生活中包含变化的内容A—能 B—基本 C—不能2.能否找到可以借助一次函数解决的问题3.能否与同学合作完成出水实验4.能否把这个变化过程用函数表达式表示5.能否画出该函数图象6.能否借助图象构造出不同的实际情景7.举手发言,积极表达自己意见A—积极 B—一般 C—不积极8.认真情况(讨论,思考)A—认真 B—一般 C—不认真9.对数学学习的好奇心与求知欲A—强 B—一般 C—不强10.克服困难的意志与自信心A—能 B—很少 C—不能
学生活动:学生经过寻找发现,确定本节课的研究内容。并经过共同商议,确定实施方案。 学生活动: 学生小组内交流讨论,确定研究哪些量之间的数量关系,确定具体实施计划及操作方法。 学生活动: 选取数据代入进行计算,从而得出函数表达式,从文字语言到数学语言的转化。 学生活动:在作图的过程中可能会作出不同的函数图象,从而明确自变量的取值范围 学生可以从不同的角度对函数图像进行分析。 学生活动:计算出一个小时水龙头的出水量,懂得节约用水。 学生活动:展开充分的想象,可以从身边事入手。 学生有选择的进行课后巩固。
【内容解析】 《课标》在教学建议中指出,要重视对教学内容的整体分析,帮助学生建立能体现数学学科的本质,对未来学习有支撑意义的结构化的数学知识体系。函数是中学数学的重要内容,它不仅是后继学习数学的基础,同时在物理、化学等自然学科中有着广泛应用。在解决生产生活中的问题时,也往往采用函数作为建立模型的基本工具。 单元教学内容框架 课程标准表述 能根据简单实际问题中的已知条件确定一次函数的表达式;会在不同问题情境中运用待定系数法确定一次函数的表达式;会画出一次函数的图象;会根据一次函数的表达式求其图象与坐标轴的交点坐标;会根据一次函数的图象和表达式y=kx+b(k≠0),探索并理解 k值的变化对函数图象的影响。认识正比例函数中两个变量之间的对应规律,会结合实例说明正比例函数的意义及变量之间的对应规律。会根据一次函数的图象解释一次函数与二元一次方程的关系;能在实际问题中列出一次函数的表达式,并结合一次函数的图象与表达式的性质等解决简单的实际问题。 关键词:概念 性质 应用 单元核心问题链 1.如何从实际问题中抽象出函数概念? 2.如何数形结合得到一次函数的性质? 3.如何用一次函数解决问题? 【目标设置】 单元目标 1.探索实例中的数量关系和变化规律,了解常量、变量的意义。理解函数的概念和三种表示法.能确定简单问题中函数自变量的取值范围,并会求出函数值. 2.结合情境体会一次函数的意义,会利用待定系数法确定一次函数的表达式. 3.能画出一次函数图象,根据一次函数图象及表达式y=kx+b(k≠0)探索并理解k>0和k<0时,图象的变化情况. 4.体会一次函数与二元一次方程的关系. 5.能用一次函数解决简单的实际问题. 单元重难点 重点:结合实例掌握一次函数的概念,结合图像讨论性质,运用一次函数的图像和性质解决实际问题; 难点:函数概念的建立和利用一次函数的图象和性质解决简单实际问题。 课时重难点 重点:建立一次函数模型解决简单实际问题; 难点:把实际问题抽象出数学问题。 课时目标 掌握从实际问题抽象函数问题的方式方法,会借助一次函数解决实际问题 经历提出问题—分析问题—解决问题的过程,培养将实际问题抽象数学问题的能力; 在建构新知识的过程中,发展应用意识和创新意识,体会数学的应用价值 教学策略 教法:采用基于问题解决的任务驱动教学方式 学法:采用自主探究、合作交流的学习方法,让学生带着问题学,在探索中学,在动手操作中学。 【教学设计】 确定研究内容 建立函数模型 利用模型解题 根据模型拓展 确定研究内容 实践探究:学生以兴趣小组的形式去主动寻找生活中变化的内容,寻找可以借助一次函数解决的问题。 等等 为了提醒人们节约用水,及时关好水龙头,班里同学分工做了水龙头出水实验,他们用于接水的量筒的最大容量为500ml。 设计意图:一次函数是刻画变化的模型,以往的教学中教师通常直接给出情景,建立模型,解决问题。但是对于生活中的情景,把生活情景数学化是难点,为了培养学生用数学的眼光观察世界的能力,设计实践探究活动,让学生去寻找和发现生活中的变化内容。在确定研究内容的过程中,培养学生发现问题、提出问题的能力。 建立函数模型 问题1、在水龙头出水的过程中涉及哪些量? 问题2、研究哪些量之间的关系? 问题3、如何测出水速度? 学生交流讨论,做水龙头流水实验。 实验:同学在做水龙头出水实验时,每隔10s观察量筒中水的体积,记录的数据如下表(出的水量精确到1ml); 通过多次测量取平均值得到下表,并填写内容。 时间t(秒)10203040506070流出的水量V(毫升)
设计意图:让学生思想的火花充分跳跃,培养学生用数学的思维思考世界的能力,在教学中引导学生得出研究对象中的函数关系:①量筒内水的体积=出水速度×出水时间;②量筒剩余容量=量筒容量-量筒内水的体积 利用模型解题 问题4、能否把变化过程用数学表达式表示? 问题5、如何更直观的反应这个变化过程? 问题6、观察一次函数图象,你能获取哪些信息? 问题7、能否用上述模型预测一个小时没关水龙头将浪费多少水资源?对此,我们应该怎么做? 设计意图:培养学生识图能力和从图像中获取信息的能力。综合与实践是促进学生深度学习、培育数学核心素养的有效途径,它具有重要的育人价值。基于单元整体视角,将综合与实践纳入单元整体设计,是实现数学综合与时间常态化实施的有效途径。 根据模型拓展 问题8、如何将这个问题情景进行迁移?(还有哪些情景可以用这个函数图象解释呢?) 设计意图:为了让学生理解一次函数可以表示一类现实事物运动变化规律,让学生在小组交流等活动,展开充分想象去构造不同的实际情景表述这个函数关系中,加深对一次函数的认识,发展几何直观,培养学生学习数学的兴趣,感悟数学与生活的密切联系。 【作业布置】 A层基础 某养猪场欲买饲料喂猪,相关数据如下表: 饲料种类/元饲料单价元/kg猪食量kg/天猪增重kg/天A2.82.51.0B2.32.50.9
由市场行情得知,屠宰场收购生猪每千克单价在10~15元范围内. (1)设收购生猪每千克单价为x元,分别列出喂A,B两种饲料的日利润y元的 函数表达式;(日利润 =日收益-日饲料成本) (2)选用哪种饲料合算 B层提升 球从高处下落再反弹起来,可以直观地看出球的下落高度越高,反弹高度也就越高,那么球下落高度与反弹高度具有怎样的关系呢 请你进行实验,将实验数据填入下表,并根据实验数据建立球下落高度和反弹高度之间关系的函数模型. 试验次数第1次第2次第3次第4次第5次第5次下落高度/cm反弹高度/cm
拓展作业 根据水龙头中的数学,完成一篇小论文 设计意图:A层重基础,B层注重提升,同时在拓展作业中以学习小组的完成水龙头中的数学的小论文。分层作业尊重学生的思维层级和个体需求。 【板书设计】 一次函数模型的应用 【教学思考】 学生对数学具有好奇心和求知欲,了解数学的价值,欣赏数学美,提高学习数学的兴趣,建立学好数学的信心,养成良好的学习习惯,形成质疑问难,自我反思和用于探索的科学精神。本节课聚焦在实践中获得知识,并由此展开教学设计,学生亲身体验,寻找生活中的一次函数,构造真实有效的情景,让学生用数学的眼光观察世界;学生观察数轴,看横轴看纵轴,看函数图象的变化趋势,经历学数学、用数学的过程,培养学生会数学的思维思考世界,用数学的思维表达世界,培养学生的核心素养;通过对一次函数构造不同的情景,抓住一次函数是两个变量之间的关系的本质,强化学生对函数模型的认识。 课堂观察检测表 学生姓名: 年级 : 观察时间: 年 月 日 因素ABC说明1.能否小组合作找的到生活中包含变化的内容A—能 B—基本 C—不能2.能否找到可以借助一次函数解决的问题3.能否与同学合作完成出水实验4.能否把这个变化过程用函数表达式表示5.能否画出该函数图象6.能否借助图象构造出不同的实际情景7.举手发言,积极表达自己意见A—积极 B—一般 C—不积极8.认真情况(讨论,思考)A—认真 B—一般 C—不认真9.对数学学习的好奇心与求知欲A—强 B—一般 C—不强10.克服困难的意志与自信心A—能 B—很少 C—不能
学生活动:学生经过寻找发现,确定本节课的研究内容。并经过共同商议,确定实施方案。 学生活动: 学生小组内交流讨论,确定研究哪些量之间的数量关系,确定具体实施计划及操作方法。 学生活动: 选取数据代入进行计算,从而得出函数表达式,从文字语言到数学语言的转化。 学生活动:在作图的过程中可能会作出不同的函数图象,从而明确自变量的取值范围 学生可以从不同的角度对函数图像进行分析。 学生活动:计算出一个小时水龙头的出水量,懂得节约用水。 学生活动:展开充分的想象,可以从身边事入手。 学生有选择的进行课后巩固。
