4.3.5 全等三角形的应用 教案(表格式)2025-2026学年八年级上册数学湘教版
文档属性
| 名称 | 4.3.5 全等三角形的应用 教案(表格式)2025-2026学年八年级上册数学湘教版 |  | |
| 格式 | docx | ||
| 文件大小 | 94.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:47:06 | ||
图片预览


文档简介
课题 第4章 4.3 全等三角形 4.3.5 全等三角形的应用
授课教师 授课类型 新授课
教学目标 1. 可以灵活构造全等三角形,将不可测距离化为可测距离; 2. 能利用三角形的全等解决实际问题; 3. 在解决问题过程中进行有条理的思考与表达. 4.经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力. 5.学生积极参与利用三角形全等解决问题的过程,从中体会证明与成功的快乐,增强学习好数学的自信心,体会三角形全等条件在现实生活中的应用价值.
教学重点、难点 教学重点:利用三角形的全等解决实际问题. 教学难点:利用三角形的全等解决实际问题.
教学方法 本节课作为全等三角形的应用课,通过对一些案例进行分析,解决生活中的实际问题,帮助学生构建系统知识体系.
教学准备 多媒体课件
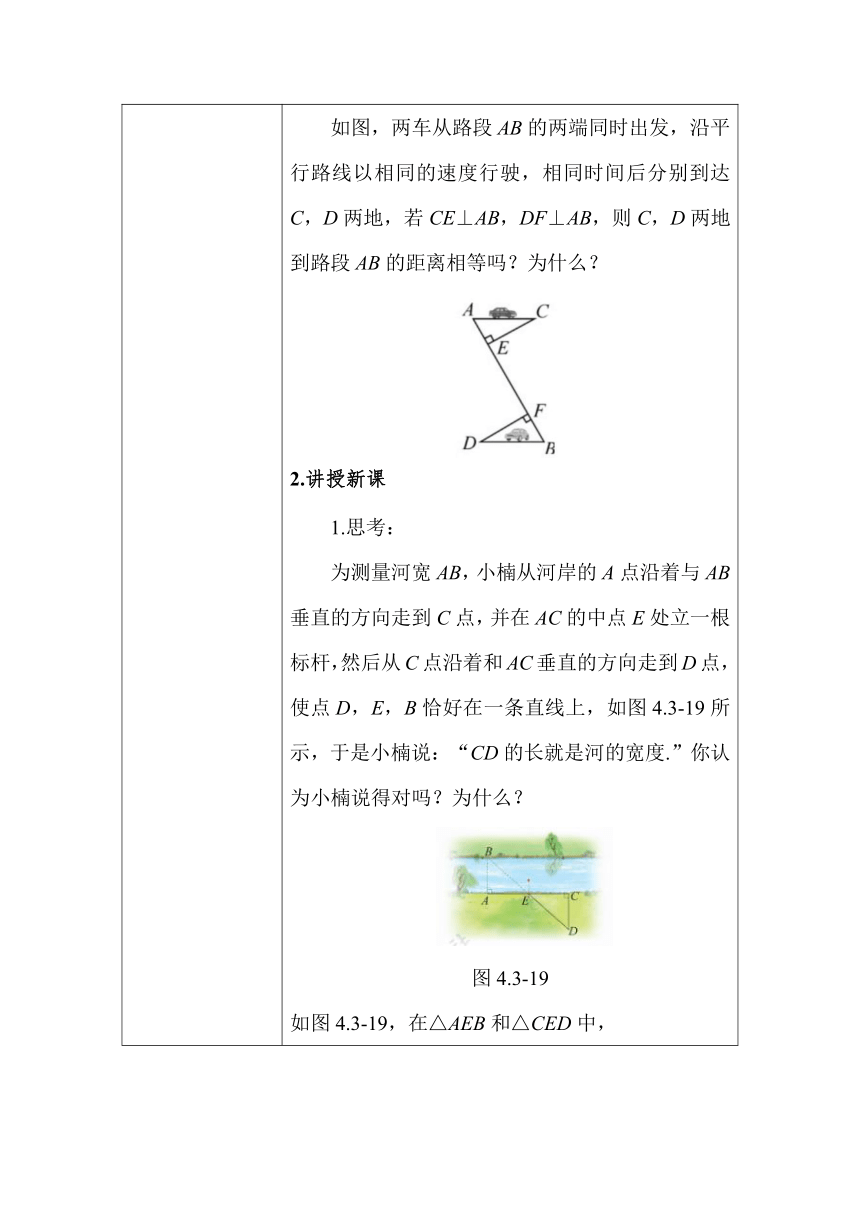
教学过程 1.新课导入 在生活中,有时可以利用全等三角形的有关知识帮助我们解决一些实际问题. 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地,若CE⊥AB,DF⊥AB,则C,D两地到路段AB的距离相等吗?为什么? 2.讲授新课 1.思考: 为测量河宽AB,小楠从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上,如图4.3-19所示,于是小楠说:“CD的长就是河的宽度.”你认为小楠说得对吗?为什么? 图4.3-19 如图4.3-19,在△AEB和△CED中, 所以△AEB≌△CED(角边角),从而AB=CD. 即CD的长就是河的宽度.因此,小楠说得对. (老师对例题进行讲解) 例8:小玲家有一个小口玻璃瓶,她想知道它的内径是多少,但是尺子不能伸到里边测量,于是她想了个办法:将两根长度相同的细木条的中点固定在一起,木条可以绕中点转动(如图4.3-20所示),使CD与瓶底平行,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道其中的理由是什么吗(木条的粗细忽略不计)? 图4.3-20 分析 只需要说明AB和CD相等即可. 解:如图4.3-20,连接AB,CD, 由题意可知,OA=OB=OC=OD. 在△AOB和△COD中, 所以△AOB≌△COD(边角边),从而AB=CD, 即AB的长等于玻璃瓶的内径, 例9:在在甲楼底部、乙楼顶部分别安装一盏射灯, 其中A灯恰好照到B灯,B灯恰好照到甲楼的顶部C处,如图4.3-21所示.已知AE为水平线,CA⊥AE, BE⊥AE,如果两盏灯的光线AB,BC与水平线的夹角相等,那么能否说甲楼高度是乙楼高度的2倍?为什么 图4.3-21 解:如图4.3-21,过点B作BF⊥AC,交AC于 点F,则∠CFB=∠AFB=90°. 又∠CFB=∠CAE=90°, 所以FB//AE,从而∠ABF=∠BAE. 因为两盏灯的光线AB,BC与水平线的夹角相等, 所以∠CBF=∠BAE,从而∠CBF=∠ABF. 在△CBF和△ABF中, 所以△CBF≌△ABF(角边角),从而CF=AF. 又FA⊥AE,BE⊥AE,且AE//FB, 所以AF,EB是平行线AE与FB的公垂线段, 故AF=EB,从而AC=2AF=2EB. 因此,可以说甲楼高度是乙楼高楼的2倍. 还有其他方法证明AF=EB吗 (学生自己写一写) 3.课堂练习 1.如图所示,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.你能说明其中的道理吗 解:在△ABC与△DEC中, 所以△ABC≌△EDC(边角边), 所以AB=DE. 4.课堂小结 证明全等三角形中常见辅助线的作法:①连接两点;②倍长中线;③过一点作已知直线的平行线;④过一点作已知直线的垂线. 把要证明的边相等或角相等,转化为证明它们所在的三角形全等.如果两个三角形全等的条件不具备,可通过两次或多次三角形全等得出. 5.板书设计 利用三角形全等解决生活中的问题
教学设计反思 本节课学习了利用全等三角形解决问题方法,让学生积极主动地去练习,学会分析已知什么,要证明什么,还需要什么条件,同时还要善于从图形中发现隐含的条件:公共边、公共角、对顶角、邻补角等.
授课教师 授课类型 新授课
教学目标 1. 可以灵活构造全等三角形,将不可测距离化为可测距离; 2. 能利用三角形的全等解决实际问题; 3. 在解决问题过程中进行有条理的思考与表达. 4.经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力. 5.学生积极参与利用三角形全等解决问题的过程,从中体会证明与成功的快乐,增强学习好数学的自信心,体会三角形全等条件在现实生活中的应用价值.
教学重点、难点 教学重点:利用三角形的全等解决实际问题. 教学难点:利用三角形的全等解决实际问题.
教学方法 本节课作为全等三角形的应用课,通过对一些案例进行分析,解决生活中的实际问题,帮助学生构建系统知识体系.
教学准备 多媒体课件
教学过程 1.新课导入 在生活中,有时可以利用全等三角形的有关知识帮助我们解决一些实际问题. 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地,若CE⊥AB,DF⊥AB,则C,D两地到路段AB的距离相等吗?为什么? 2.讲授新课 1.思考: 为测量河宽AB,小楠从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上,如图4.3-19所示,于是小楠说:“CD的长就是河的宽度.”你认为小楠说得对吗?为什么? 图4.3-19 如图4.3-19,在△AEB和△CED中, 所以△AEB≌△CED(角边角),从而AB=CD. 即CD的长就是河的宽度.因此,小楠说得对. (老师对例题进行讲解) 例8:小玲家有一个小口玻璃瓶,她想知道它的内径是多少,但是尺子不能伸到里边测量,于是她想了个办法:将两根长度相同的细木条的中点固定在一起,木条可以绕中点转动(如图4.3-20所示),使CD与瓶底平行,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道其中的理由是什么吗(木条的粗细忽略不计)? 图4.3-20 分析 只需要说明AB和CD相等即可. 解:如图4.3-20,连接AB,CD, 由题意可知,OA=OB=OC=OD. 在△AOB和△COD中, 所以△AOB≌△COD(边角边),从而AB=CD, 即AB的长等于玻璃瓶的内径, 例9:在在甲楼底部、乙楼顶部分别安装一盏射灯, 其中A灯恰好照到B灯,B灯恰好照到甲楼的顶部C处,如图4.3-21所示.已知AE为水平线,CA⊥AE, BE⊥AE,如果两盏灯的光线AB,BC与水平线的夹角相等,那么能否说甲楼高度是乙楼高度的2倍?为什么 图4.3-21 解:如图4.3-21,过点B作BF⊥AC,交AC于 点F,则∠CFB=∠AFB=90°. 又∠CFB=∠CAE=90°, 所以FB//AE,从而∠ABF=∠BAE. 因为两盏灯的光线AB,BC与水平线的夹角相等, 所以∠CBF=∠BAE,从而∠CBF=∠ABF. 在△CBF和△ABF中, 所以△CBF≌△ABF(角边角),从而CF=AF. 又FA⊥AE,BE⊥AE,且AE//FB, 所以AF,EB是平行线AE与FB的公垂线段, 故AF=EB,从而AC=2AF=2EB. 因此,可以说甲楼高度是乙楼高楼的2倍. 还有其他方法证明AF=EB吗 (学生自己写一写) 3.课堂练习 1.如图所示,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离但绳子不够长,一个叔叔帮他出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.你能说明其中的道理吗 解:在△ABC与△DEC中, 所以△ABC≌△EDC(边角边), 所以AB=DE. 4.课堂小结 证明全等三角形中常见辅助线的作法:①连接两点;②倍长中线;③过一点作已知直线的平行线;④过一点作已知直线的垂线. 把要证明的边相等或角相等,转化为证明它们所在的三角形全等.如果两个三角形全等的条件不具备,可通过两次或多次三角形全等得出. 5.板书设计 利用三角形全等解决生活中的问题
教学设计反思 本节课学习了利用全等三角形解决问题方法,让学生积极主动地去练习,学会分析已知什么,要证明什么,还需要什么条件,同时还要善于从图形中发现隐含的条件:公共边、公共角、对顶角、邻补角等.
同课章节目录
