5.1 直角三角形的性质定理 第1课时 直角三角形的性质 教案(表格式)2025-2026学年八年级上册数学湘教版
文档属性
| 名称 | 5.1 直角三角形的性质定理 第1课时 直角三角形的性质 教案(表格式)2025-2026学年八年级上册数学湘教版 |  | |
| 格式 | docx | ||
| 文件大小 | 214.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:50:02 | ||
图片预览




文档简介
课题 第5章 5.1 直角三角形的性质定理 第1课时 直角三角形的性质
授课教师 授课类型 新授课
教学目标 1.体验直角三角形应用的广泛性,理解直角三角形的定义,进一步认识直角三角形; 2.经历“直角三角形两个锐角互余”的探讨,掌握直角三角形两个锐角互余的性质; 3.会用“两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形; 4.理解和掌握直角三角形性质定理:直角三角形斜边上的中线等于斜边的一半. 5.通过动手,猜想发现直角三角形的性质,引导逆向思维,探索性质的推导方法——同一法. 6.体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
教学重点、 难点 教学重点:直角三角形性质和判定的探索及运用. 教学难点:直角三角形性质“斜边上的中线等于斜边的一半”的判定探索过程.
教学准备 多媒体课件、三角尺
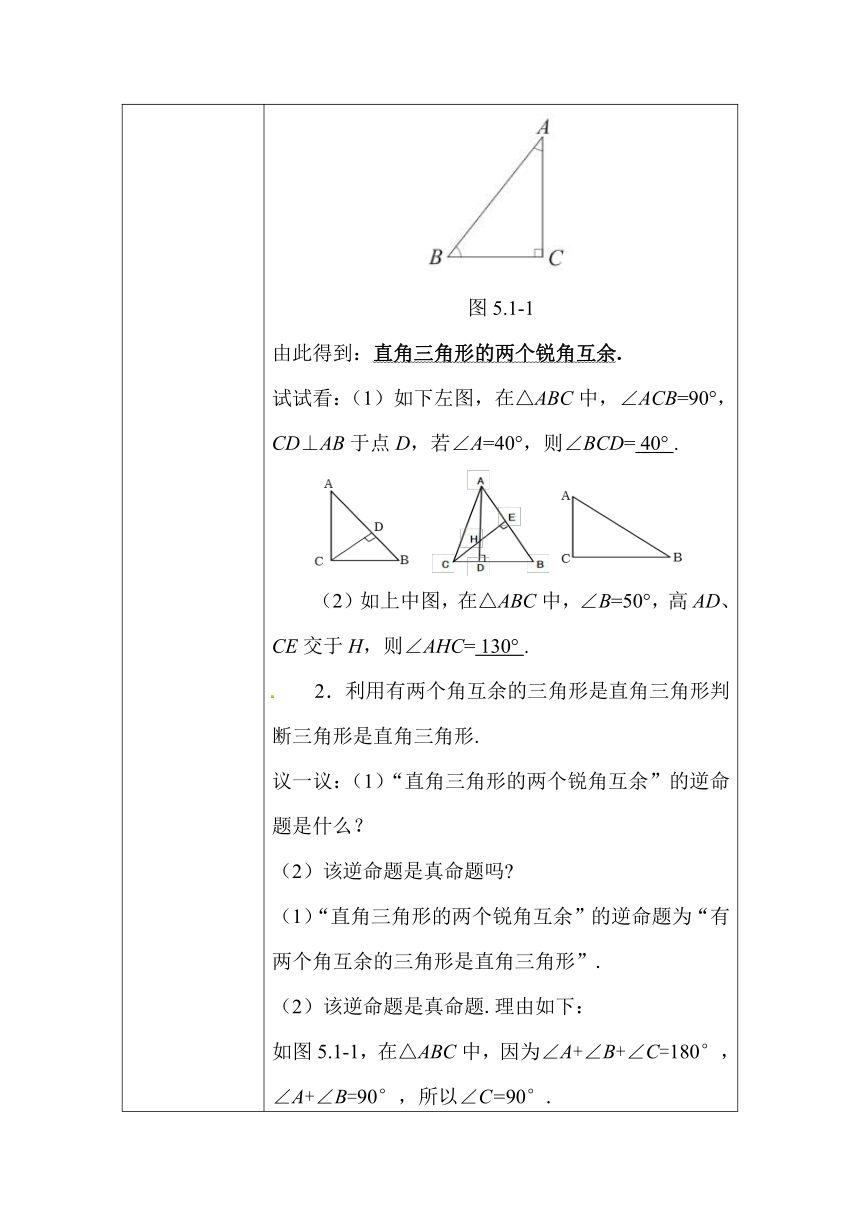
教学过程 1.情境导入 在小学时我们已经学习过有关直角三角形的知识. 问:什么叫直角三角形? 有一个角是直角的三角形是直角三角形. 同学们可以用手上的三角板和量角器作一个直角三角形. 观察所画的直角三角形,然后思考:从定义可以知道直角三角形具有一个角是直角的性质,要判断一个三角形是直角三角形需要判断这个三角形中有一个角是直角.直角三角形除了有一个角是直角这条性质外还有没有别的性质呢?判断一个三角形是直角三角形除了判断一个角是直角还有没有别的方法呢?从这节课起我们就来探究这些问题. 2.讲授新课 1.直角三角形的两个锐角互余 说一说: 在Rt△ABC中,若∠C=90°,则∠A+∠B=? 如图5.1-1,在Rt△ABC中,因为∠C=90°,由三角形内角和定理可得:∠A+∠B=90°. 图5.1-1 由此得到:直角三角形的两个锐角互余. 试试看:(1)如下左图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,则∠BCD= 40° . (2)如上中图,在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC= 130° . 2.利用有两个角互余的三角形是直角三角形判断三角形是直角三角形. 议一议:(1)“直角三角形的两个锐角互余”的逆命题是什么? (2)该逆命题是真命题吗 (1)“直角三角形的两个锐角互余”的逆命题为“有两个角互余的三角形是直角三角形”. (2)该逆命题是真命题.理由如下: 如图5.1-1,在△ABC中,因为∠A+∠B+∠C=180°,∠A+∠B=90°,所以∠C=90°. 因此,△ABC是直角三角形. 由此得到:有两个角互余的三角形是直角三角形. 试试看:如图,AB∥CD,∠A和∠C的平分线相交于H点,那么△ABC是直角三角形吗?为什么? 是,理由:因为AB∥CD,所以∠BAC+∠ACD=180°. 因为AH平分∠BAC,CH平分∠ACD, 所以∠CAH=∠BAC,∠ACH=∠ACD, 所以∠CAH+∠ACH=(∠BAC+∠ACD)=×180°=90°. 所以△AHC是直角三角形. 3.直角三角形斜边上的中线等于斜边的一半的探索过程 思考:如图5.1-2,用三角板画一个Rt△ABC,取线段AB的中点D,连接DC.以点D为圆心,DB为半径画圆弧,则所画的弧经过点C吗?DC与AB之间有怎样的数量关系 图5.1-2 可以发现,该弧经过点C,且DC=DB= AB. (4)寻找理论依据: I.你能用符号表示上面问题中的条件和结论吗? 已知:Rt△ABC中,∠C=90°,CD是中线. 问:CD=AB吗? II.分析:如图5.1-3,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线. 过点D作DE//BC,DF//AC,分别交AC,BC于点E,F,于是∠ADE=∠B,∠AED=∠ACB=90°,∠FDC=∠ECD,∠DFB=∠ACB=90°. 图5.1-3 在△ADE与△DBF中, 所以△ADE≌△DBF(角角边),从而DE=BF. ① 在△DFC与△CED中, 所以△DFC≌∠CED(角角边),从而CF=DE. ② 由①式和②式得,CF=BF. 因此,直线DF是线段BC的垂直平分线. 根据线段垂直平分线的性质定理得,DC=DB. 因此DC=DB=AB. 归纳: 直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半. 4.逆向思考: 如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形吗?为什么?(交流讨论) 例1:如图5.1-4,已知CD是△ABC的边AB上的中线,且CD=AB.求证:△ABC是直角三角形. 图5.1-4 证明:因为CD=AB=AD=BD, 所以∠1=∠A,∠2=∠B. 因为∠A+∠B+∠ACB=180°,∠ACB=∠1+∠2, 所以∠A+∠B+∠1+∠2=180, 从而2(∠A+∠B)=180°. 因此∠A+∠B=90°. 所以△ABC是直角三角形. 归纳:若三角形一条边上的中线等于这条边长的一半,那么这个三角形是直角三角形. 3.课堂练习 1.如图,在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,交BC于F,交AB于点E.求证:FC=2BF. 证明:如图,取CF的中点M,连接AF、AM. 因为EF是AB的垂直平分线,所以AF=BF, 所以∠BAF=∠B. 因为AB=AC,∠BAC=120°, 所以∠B=∠BAF=∠C=(180°-120°)=30°, 所以∠FAC=∠BAC-∠BAF=90°. 在Rt△AFC中,∠C=30°,M为CF的中点, 所以∠AFM=60°,AM=FC=FM, 所以△AFM为等边三角形,所以AF=AM=FC. 又BF=AF,所以BF=FC,即FC=2BF. 方法总结:当已知条件中出现直角三角形斜边上的中线时,通常会运用到“直角三角形斜边上的中线等于斜边的一半”这个性质,使用该性质时,要注意找准斜边和斜边上的中线. 2.如图所示,四个小朋友在操场上做抢球游戏,他们分别站在四个直角三角形的直角顶点A、B、C、D处,球放在EF的中点O处,则游戏 公平 (填“公平”或“不公平”). 解析:游戏是否公平就是判断点A、B、C、D到点O的距离是否相等.四个直角三角形有公共的斜边EF,且O为斜边EF的中点.连接OA、OB、OC、OD.根据“直角三角形斜边上的中线等于斜边的一半”的性质可知,OA=OB=OC=OD=EF,即点A、B、C、D到O的距离相等.由此可得出结论:游戏公平. 方法总结:题目中如果出现“直角三角形”和“中点”这两个条件时,应连接直角顶点与斜边中点,再利用“斜边上的中线等于斜边的一半的性质”解题. 3.如图所示,在Rt△ABC中,AB=AC,∠BAC= 90°,O为BC的中点. (1)写出点O到△ABC的三个顶点A、B、C的距离的数量关系; (2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM.请判断△OMN的形状,并证明你的结论. 解:(1)连接AO,如图, 在Rt△ABC中,∠BAC=90°,O为BC的中点, 所以OA=BC=OB=OC,即OA=OB=OC; (2)△OMN是等腰直角三角形.理由如下: 因为AC=BA,OC=OB,∠BAC=90°, 所以OA=OB,∠NAO=∠CAB=∠B=45°,AO⊥BC, 又AN=BM,所以△AON≌△BOM, 所以ON=OM,∠NOA=∠MOB, 所以∠NOA+∠AOM=∠MOB+∠AOM, 所以∠NOM=∠AOB=90°, 所以△MON是等腰直角三角形. 方法总结:解决动态探究性问题,要把握住动态变化过程中的不变量,比如角的度数、线段的长和不变的数量关系,比如斜边上的中线等于斜边的一半,直角三角形两锐角互余. 4.课堂小结 1.直角三角形的性质: ①直角三角形的两个锐角互余. ②直角三角形斜边上的中线等于斜边的一半. 2.直角三角形的判定方法: ①有一个角是直角的三角形是直角三角形. ②有两个角互余的三角形是直角三角形. 3.直角三角形斜边中线常见类型: 5.板书设计 1.直角三角形的性质 性质一:直角三角形的两个锐角互余. 性质二:直角三角形斜边上的中线等于斜边的一半. 2.直角三角形的判定 方法一:一个角是直角的三角形是直角三角形. 方法二:两个角互余的三角形是直角三角形.
教学设计反思 通过练习反馈的情况来看,学生对于利用已知条件判定一个三角形是否为直角三角形这一考点比较容易上手一些,而往往忽略在直角三角形中告诉斜边上的中点利用中线这一性质解决问题.在今后的教学中应让学生不断强化提高这一点.
授课教师 授课类型 新授课
教学目标 1.体验直角三角形应用的广泛性,理解直角三角形的定义,进一步认识直角三角形; 2.经历“直角三角形两个锐角互余”的探讨,掌握直角三角形两个锐角互余的性质; 3.会用“两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形; 4.理解和掌握直角三角形性质定理:直角三角形斜边上的中线等于斜边的一半. 5.通过动手,猜想发现直角三角形的性质,引导逆向思维,探索性质的推导方法——同一法. 6.体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
教学重点、 难点 教学重点:直角三角形性质和判定的探索及运用. 教学难点:直角三角形性质“斜边上的中线等于斜边的一半”的判定探索过程.
教学准备 多媒体课件、三角尺
教学过程 1.情境导入 在小学时我们已经学习过有关直角三角形的知识. 问:什么叫直角三角形? 有一个角是直角的三角形是直角三角形. 同学们可以用手上的三角板和量角器作一个直角三角形. 观察所画的直角三角形,然后思考:从定义可以知道直角三角形具有一个角是直角的性质,要判断一个三角形是直角三角形需要判断这个三角形中有一个角是直角.直角三角形除了有一个角是直角这条性质外还有没有别的性质呢?判断一个三角形是直角三角形除了判断一个角是直角还有没有别的方法呢?从这节课起我们就来探究这些问题. 2.讲授新课 1.直角三角形的两个锐角互余 说一说: 在Rt△ABC中,若∠C=90°,则∠A+∠B=? 如图5.1-1,在Rt△ABC中,因为∠C=90°,由三角形内角和定理可得:∠A+∠B=90°. 图5.1-1 由此得到:直角三角形的两个锐角互余. 试试看:(1)如下左图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,则∠BCD= 40° . (2)如上中图,在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC= 130° . 2.利用有两个角互余的三角形是直角三角形判断三角形是直角三角形. 议一议:(1)“直角三角形的两个锐角互余”的逆命题是什么? (2)该逆命题是真命题吗 (1)“直角三角形的两个锐角互余”的逆命题为“有两个角互余的三角形是直角三角形”. (2)该逆命题是真命题.理由如下: 如图5.1-1,在△ABC中,因为∠A+∠B+∠C=180°,∠A+∠B=90°,所以∠C=90°. 因此,△ABC是直角三角形. 由此得到:有两个角互余的三角形是直角三角形. 试试看:如图,AB∥CD,∠A和∠C的平分线相交于H点,那么△ABC是直角三角形吗?为什么? 是,理由:因为AB∥CD,所以∠BAC+∠ACD=180°. 因为AH平分∠BAC,CH平分∠ACD, 所以∠CAH=∠BAC,∠ACH=∠ACD, 所以∠CAH+∠ACH=(∠BAC+∠ACD)=×180°=90°. 所以△AHC是直角三角形. 3.直角三角形斜边上的中线等于斜边的一半的探索过程 思考:如图5.1-2,用三角板画一个Rt△ABC,取线段AB的中点D,连接DC.以点D为圆心,DB为半径画圆弧,则所画的弧经过点C吗?DC与AB之间有怎样的数量关系 图5.1-2 可以发现,该弧经过点C,且DC=DB= AB. (4)寻找理论依据: I.你能用符号表示上面问题中的条件和结论吗? 已知:Rt△ABC中,∠C=90°,CD是中线. 问:CD=AB吗? II.分析:如图5.1-3,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线. 过点D作DE//BC,DF//AC,分别交AC,BC于点E,F,于是∠ADE=∠B,∠AED=∠ACB=90°,∠FDC=∠ECD,∠DFB=∠ACB=90°. 图5.1-3 在△ADE与△DBF中, 所以△ADE≌△DBF(角角边),从而DE=BF. ① 在△DFC与△CED中, 所以△DFC≌∠CED(角角边),从而CF=DE. ② 由①式和②式得,CF=BF. 因此,直线DF是线段BC的垂直平分线. 根据线段垂直平分线的性质定理得,DC=DB. 因此DC=DB=AB. 归纳: 直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半. 4.逆向思考: 如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形吗?为什么?(交流讨论) 例1:如图5.1-4,已知CD是△ABC的边AB上的中线,且CD=AB.求证:△ABC是直角三角形. 图5.1-4 证明:因为CD=AB=AD=BD, 所以∠1=∠A,∠2=∠B. 因为∠A+∠B+∠ACB=180°,∠ACB=∠1+∠2, 所以∠A+∠B+∠1+∠2=180, 从而2(∠A+∠B)=180°. 因此∠A+∠B=90°. 所以△ABC是直角三角形. 归纳:若三角形一条边上的中线等于这条边长的一半,那么这个三角形是直角三角形. 3.课堂练习 1.如图,在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,交BC于F,交AB于点E.求证:FC=2BF. 证明:如图,取CF的中点M,连接AF、AM. 因为EF是AB的垂直平分线,所以AF=BF, 所以∠BAF=∠B. 因为AB=AC,∠BAC=120°, 所以∠B=∠BAF=∠C=(180°-120°)=30°, 所以∠FAC=∠BAC-∠BAF=90°. 在Rt△AFC中,∠C=30°,M为CF的中点, 所以∠AFM=60°,AM=FC=FM, 所以△AFM为等边三角形,所以AF=AM=FC. 又BF=AF,所以BF=FC,即FC=2BF. 方法总结:当已知条件中出现直角三角形斜边上的中线时,通常会运用到“直角三角形斜边上的中线等于斜边的一半”这个性质,使用该性质时,要注意找准斜边和斜边上的中线. 2.如图所示,四个小朋友在操场上做抢球游戏,他们分别站在四个直角三角形的直角顶点A、B、C、D处,球放在EF的中点O处,则游戏 公平 (填“公平”或“不公平”). 解析:游戏是否公平就是判断点A、B、C、D到点O的距离是否相等.四个直角三角形有公共的斜边EF,且O为斜边EF的中点.连接OA、OB、OC、OD.根据“直角三角形斜边上的中线等于斜边的一半”的性质可知,OA=OB=OC=OD=EF,即点A、B、C、D到O的距离相等.由此可得出结论:游戏公平. 方法总结:题目中如果出现“直角三角形”和“中点”这两个条件时,应连接直角顶点与斜边中点,再利用“斜边上的中线等于斜边的一半的性质”解题. 3.如图所示,在Rt△ABC中,AB=AC,∠BAC= 90°,O为BC的中点. (1)写出点O到△ABC的三个顶点A、B、C的距离的数量关系; (2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM.请判断△OMN的形状,并证明你的结论. 解:(1)连接AO,如图, 在Rt△ABC中,∠BAC=90°,O为BC的中点, 所以OA=BC=OB=OC,即OA=OB=OC; (2)△OMN是等腰直角三角形.理由如下: 因为AC=BA,OC=OB,∠BAC=90°, 所以OA=OB,∠NAO=∠CAB=∠B=45°,AO⊥BC, 又AN=BM,所以△AON≌△BOM, 所以ON=OM,∠NOA=∠MOB, 所以∠NOA+∠AOM=∠MOB+∠AOM, 所以∠NOM=∠AOB=90°, 所以△MON是等腰直角三角形. 方法总结:解决动态探究性问题,要把握住动态变化过程中的不变量,比如角的度数、线段的长和不变的数量关系,比如斜边上的中线等于斜边的一半,直角三角形两锐角互余. 4.课堂小结 1.直角三角形的性质: ①直角三角形的两个锐角互余. ②直角三角形斜边上的中线等于斜边的一半. 2.直角三角形的判定方法: ①有一个角是直角的三角形是直角三角形. ②有两个角互余的三角形是直角三角形. 3.直角三角形斜边中线常见类型: 5.板书设计 1.直角三角形的性质 性质一:直角三角形的两个锐角互余. 性质二:直角三角形斜边上的中线等于斜边的一半. 2.直角三角形的判定 方法一:一个角是直角的三角形是直角三角形. 方法二:两个角互余的三角形是直角三角形.
教学设计反思 通过练习反馈的情况来看,学生对于利用已知条件判定一个三角形是否为直角三角形这一考点比较容易上手一些,而往往忽略在直角三角形中告诉斜边上的中点利用中线这一性质解决问题.在今后的教学中应让学生不断强化提高这一点.
同课章节目录
