5.2 勾股定理及其逆定理 第1课时 勾股定理 教案(表格式)2025-2026学年八年级上册数学湘教版
文档属性
| 名称 | 5.2 勾股定理及其逆定理 第1课时 勾股定理 教案(表格式)2025-2026学年八年级上册数学湘教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 276.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览



文档简介
课题 第5章 5.2 勾股定理及其逆定理 第1课时 勾股定理
授课教师 授课类型 新授课
教学目标 1.让学生体验勾股定理的探索过程; 2.掌握勾股定理; 3.学会用勾股定理解决简单的几何问题. 4.经历操作、归纳和猜想,用面积法推导作出肯定结论的过程,来了解勾股定理. 5.了解我国古代数学家发现、推导和应用勾股定理中的贡献与成就,增进爱国主义情感,体验探索发现的过程和知识运用,增强学习数学的自信.
教学重点、 难点 教学重点:勾股定理的证明及简单应用. 教学难点:勾股定理的证明.
教学准备 多媒体课件、三角尺
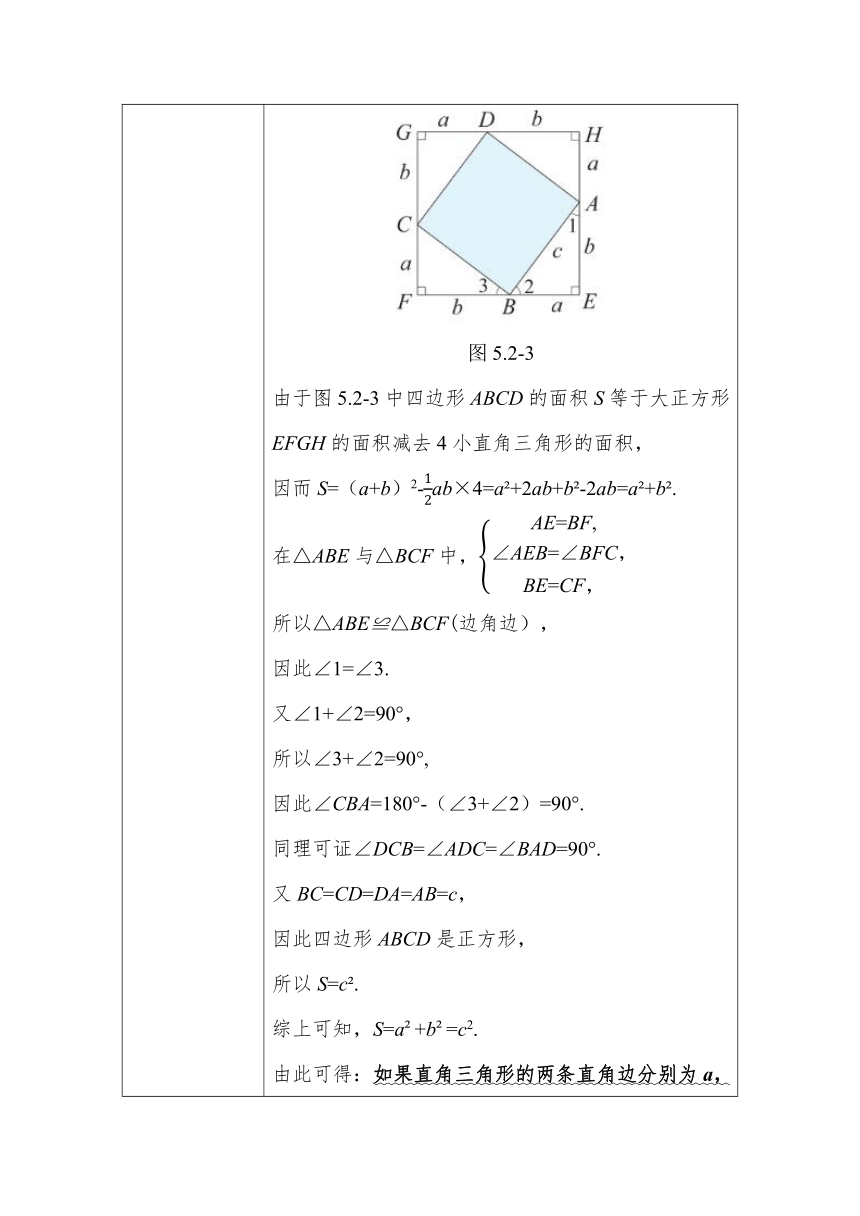
教学过程 1.情境导入 1.2002年国际数学家大会于8月20日~28日在我国北京召开,这是全球数学界水平最高的盛会.本届国际数学大会(ICM-2002)的会标图徽如下左图所示,取材于我国古代数学家赵爽所著的《勾股圆方图注》,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.你知道会标的含义吗? 2.如上右图所示的图形像一棵枝叶茂盛、姿态优美的树,这就是著名的毕达哥拉斯树,它由若干个图形组成,而每个图形的基本元素是三个正方形和一个直角三角形.各组图形大小不一,但形状一致,结构奇巧.你能说说其中的奥秘吗? 3.我们知道,在直角三角形中,30角所对的直角边等于斜边的一半,那么任意直角三角形三边的长度之间是否存在数量关系?下面来进行研究. 2.讲授新课 1.观察 如图5.2-1,在方格纸上(设小方格的边长为1)画一个顶点都在格点上的Rt△ABC,使其两直角边分别为3,4,将斜边AB绕点A旋转,使其处于水平位置,你发现这条斜边的长度是多少? 图5.2-1 可以发现,两直角边分别为3,4的直角三角形,其斜边为5. 2.议一议 我国古代数学名著《周髀算经》,把直角三角形较短的直角边叫作勾,较长的直角边叫作股,斜边叫作弦,并提出“勾三股四弦五”(如图5.2-2).这本著作还指出:勾与股的平方和等于弦的平方,对于这一结论,古人称为勾股算法,实际上,这一结论揭示的是直角三角形三边长的平方关系. 图5.2-2 在图形交流的基础上,老师板书:直角三角形的两直角边的平方和等于斜边的平方. 3.想一想 由于正方形的面积等于其边长的平方,于是可以借助正方形探究这一结论. 探究: 画一个边长为a+b的正方形,将其分割成4个小直角三角形和一个四边形,其中小直角三角形的两直角边都分别为a,b,斜边都为c,如图5.2-3所示.由此,你能探索出a +b =c2这一结论吗 图5.2-3 由于图5.2-3中四边形ABCD的面积S等于大正方形EFGH的面积减去4小直角三角形的面积, 因而S=(a+b)2-ab×4=a +2ab+b -2ab=a +b . 在△ABE与△BCF中, 所以△ABE≌△BCF(边角边), 因此∠1=∠3. 又∠1+∠2=90°, 所以∠3+∠2=90°, 因此∠CBA=180°-(∠3+∠2)=90°. 同理可证∠DCB=∠ADC=∠BAD=90°. 又BC=CD=DA=AB=c, 因此四边形ABCD是正方形, 所以S=c . 综上可知,S=a +b =c2. 由此可得:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a +b =c2. 这一结论称为勾股定理. 4.做一做 试通过图5.2-4中两个边长为a+b的正方形的面积表达式,验证勾股定理. 由5.2-4中的图(1)得:S大正方形=(a + b)2 , S大正方形= S长方形①+ S小正方形②+S长方形③+ S小正方形④=ab + a2+ab+b2=a2+b2+ 2ab.所以 (a + b)2=a2 + b2 + 2ab. 由5.2-4中的图(2)得:S大正方形= 4S直角三角形+ S小正方形= 4×ab + c2= c2 + 2ab.所以 a2 + b2 + 2ab =c2 + 2ab.所以a2+b2 =c2. 5. 用一用 勾股定理揭示了直角三角形三边之间的关系.在直角三角形中,若已知直角三角形任意两条边长,我们可以根据勾股定理,求出第三边的长.通过例题的讲练使学生体验勾股定理应用的普遍性和广泛性. 例1:在△ABC中,已知∠C=90°,BC=a, AC=b,AB=c. (1)若a=1,b=2,求c. (2)若a=15,c=17,求b. 让学生独立完成这个基本训练,但教师应强调解题过程的规范表述. 解:(1)根据勾股定理得,c2===5. 因为c>0,所以c=. (2)根据勾股定理得,b2===64. 因为b>0,所以b=8. 例3:如图5.2-5,已知在等腰三角形ABC中,已知AB=AC=13,BC=10,AD是底边BC上的高线,求AD的长. 图5.2-5 解:根据等腰三角形的性质定理得,AD也是底边BC上的中线,因此BD=BC=5. 在Rt△ADB中,由勾股定理得,AD2+BD2=AB2, 因此AD===12. 故AD的长为12. 3.课堂练习 探索与研究: 方法1:如图.对任意的符合条件的直角三角形ABC绕其顶点A旋转90°得直角三角形AED,所以∠BAE =90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和.根据图示写出证明勾股定理的过程; 方法2:如图.任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗? 解:方法1:S正方形ACFD=S四边形ABFE=S△BAE+S△BFE,即b2=c2+(b+a)(b-a),整理得2b2=c2+b2-a2,∴a2+b2=c2; 方法2:S四边形ABCD=S△ABC+S△ACD,S四边形ABCD=S△ABD+ S△BCD,即S△ABC+S△ACD=S△ABD+S△BCD,即b2+ab=c2+ a(b-a),整理得b2+ab=c2+a(b-a),b2+ab=c2+ab-a2,∴a2+b2=c2. 方法总结:证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理证明勾股定理. 4.课堂小结 勾股定理:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. 解题策略: 1.已知直角三角形两直角边a,b的长,求斜边c上的高h:先根据勾股定理求出斜边长c,再利用面积法得ab=ch,所以h=. 2.勾股图中的面积关系;如图,以直角三角形的三边为基础,向外作正方形、半圆、等腰直角三角形和等边三角形,它们都具有相同的结论,即S3=S1+S2.
易错提醒:运用勾股定理崇求长度时,若直角边、斜边不明确,需分类讨论,再运用勾股定理求第三条边. 5.板书设计 1.勾股定理 如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. 2.勾股定理的应用 3.勾股定理与图形的面积
教学设计反思 课堂教学中,要注意调动学生的积极性.让学生满怀激情地投入到学习中,提高课堂效率.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,可设计拼图活动,并自制精巧的课件让学生从图形上感知,再层层设问,从面积(数)入手,师生共同探究突破本节课的难点.
授课教师 授课类型 新授课
教学目标 1.让学生体验勾股定理的探索过程; 2.掌握勾股定理; 3.学会用勾股定理解决简单的几何问题. 4.经历操作、归纳和猜想,用面积法推导作出肯定结论的过程,来了解勾股定理. 5.了解我国古代数学家发现、推导和应用勾股定理中的贡献与成就,增进爱国主义情感,体验探索发现的过程和知识运用,增强学习数学的自信.
教学重点、 难点 教学重点:勾股定理的证明及简单应用. 教学难点:勾股定理的证明.
教学准备 多媒体课件、三角尺
教学过程 1.情境导入 1.2002年国际数学家大会于8月20日~28日在我国北京召开,这是全球数学界水平最高的盛会.本届国际数学大会(ICM-2002)的会标图徽如下左图所示,取材于我国古代数学家赵爽所著的《勾股圆方图注》,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.你知道会标的含义吗? 2.如上右图所示的图形像一棵枝叶茂盛、姿态优美的树,这就是著名的毕达哥拉斯树,它由若干个图形组成,而每个图形的基本元素是三个正方形和一个直角三角形.各组图形大小不一,但形状一致,结构奇巧.你能说说其中的奥秘吗? 3.我们知道,在直角三角形中,30角所对的直角边等于斜边的一半,那么任意直角三角形三边的长度之间是否存在数量关系?下面来进行研究. 2.讲授新课 1.观察 如图5.2-1,在方格纸上(设小方格的边长为1)画一个顶点都在格点上的Rt△ABC,使其两直角边分别为3,4,将斜边AB绕点A旋转,使其处于水平位置,你发现这条斜边的长度是多少? 图5.2-1 可以发现,两直角边分别为3,4的直角三角形,其斜边为5. 2.议一议 我国古代数学名著《周髀算经》,把直角三角形较短的直角边叫作勾,较长的直角边叫作股,斜边叫作弦,并提出“勾三股四弦五”(如图5.2-2).这本著作还指出:勾与股的平方和等于弦的平方,对于这一结论,古人称为勾股算法,实际上,这一结论揭示的是直角三角形三边长的平方关系. 图5.2-2 在图形交流的基础上,老师板书:直角三角形的两直角边的平方和等于斜边的平方. 3.想一想 由于正方形的面积等于其边长的平方,于是可以借助正方形探究这一结论. 探究: 画一个边长为a+b的正方形,将其分割成4个小直角三角形和一个四边形,其中小直角三角形的两直角边都分别为a,b,斜边都为c,如图5.2-3所示.由此,你能探索出a +b =c2这一结论吗 图5.2-3 由于图5.2-3中四边形ABCD的面积S等于大正方形EFGH的面积减去4小直角三角形的面积, 因而S=(a+b)2-ab×4=a +2ab+b -2ab=a +b . 在△ABE与△BCF中, 所以△ABE≌△BCF(边角边), 因此∠1=∠3. 又∠1+∠2=90°, 所以∠3+∠2=90°, 因此∠CBA=180°-(∠3+∠2)=90°. 同理可证∠DCB=∠ADC=∠BAD=90°. 又BC=CD=DA=AB=c, 因此四边形ABCD是正方形, 所以S=c . 综上可知,S=a +b =c2. 由此可得:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a +b =c2. 这一结论称为勾股定理. 4.做一做 试通过图5.2-4中两个边长为a+b的正方形的面积表达式,验证勾股定理. 由5.2-4中的图(1)得:S大正方形=(a + b)2 , S大正方形= S长方形①+ S小正方形②+S长方形③+ S小正方形④=ab + a2+ab+b2=a2+b2+ 2ab.所以 (a + b)2=a2 + b2 + 2ab. 由5.2-4中的图(2)得:S大正方形= 4S直角三角形+ S小正方形= 4×ab + c2= c2 + 2ab.所以 a2 + b2 + 2ab =c2 + 2ab.所以a2+b2 =c2. 5. 用一用 勾股定理揭示了直角三角形三边之间的关系.在直角三角形中,若已知直角三角形任意两条边长,我们可以根据勾股定理,求出第三边的长.通过例题的讲练使学生体验勾股定理应用的普遍性和广泛性. 例1:在△ABC中,已知∠C=90°,BC=a, AC=b,AB=c. (1)若a=1,b=2,求c. (2)若a=15,c=17,求b. 让学生独立完成这个基本训练,但教师应强调解题过程的规范表述. 解:(1)根据勾股定理得,c2===5. 因为c>0,所以c=. (2)根据勾股定理得,b2===64. 因为b>0,所以b=8. 例3:如图5.2-5,已知在等腰三角形ABC中,已知AB=AC=13,BC=10,AD是底边BC上的高线,求AD的长. 图5.2-5 解:根据等腰三角形的性质定理得,AD也是底边BC上的中线,因此BD=BC=5. 在Rt△ADB中,由勾股定理得,AD2+BD2=AB2, 因此AD===12. 故AD的长为12. 3.课堂练习 探索与研究: 方法1:如图.对任意的符合条件的直角三角形ABC绕其顶点A旋转90°得直角三角形AED,所以∠BAE =90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和.根据图示写出证明勾股定理的过程; 方法2:如图.任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗? 解:方法1:S正方形ACFD=S四边形ABFE=S△BAE+S△BFE,即b2=c2+(b+a)(b-a),整理得2b2=c2+b2-a2,∴a2+b2=c2; 方法2:S四边形ABCD=S△ABC+S△ACD,S四边形ABCD=S△ABD+ S△BCD,即S△ABC+S△ACD=S△ABD+S△BCD,即b2+ab=c2+ a(b-a),整理得b2+ab=c2+a(b-a),b2+ab=c2+ab-a2,∴a2+b2=c2. 方法总结:证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理证明勾股定理. 4.课堂小结 勾股定理:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. 解题策略: 1.已知直角三角形两直角边a,b的长,求斜边c上的高h:先根据勾股定理求出斜边长c,再利用面积法得ab=ch,所以h=. 2.勾股图中的面积关系;如图,以直角三角形的三边为基础,向外作正方形、半圆、等腰直角三角形和等边三角形,它们都具有相同的结论,即S3=S1+S2.
易错提醒:运用勾股定理崇求长度时,若直角边、斜边不明确,需分类讨论,再运用勾股定理求第三条边. 5.板书设计 1.勾股定理 如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. 2.勾股定理的应用 3.勾股定理与图形的面积
教学设计反思 课堂教学中,要注意调动学生的积极性.让学生满怀激情地投入到学习中,提高课堂效率.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,可设计拼图活动,并自制精巧的课件让学生从图形上感知,再层层设问,从面积(数)入手,师生共同探究突破本节课的难点.
同课章节目录
