5.2 勾股定理及其逆定理 第2课时 勾股定理的应用 教案(表格式)2025-2026学年八年级上册数学湘教版
文档属性
| 名称 | 5.2 勾股定理及其逆定理 第2课时 勾股定理的应用 教案(表格式)2025-2026学年八年级上册数学湘教版 |  | |
| 格式 | docx | ||
| 文件大小 | 573.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:51:21 | ||
图片预览



文档简介
课题 第5章 5.2 勾股定理及其逆定理 第2课时 勾股定理的应用
授课教师 授课类型 新授课
教学目标 1.会用勾股定理来解决一些实际问题,体会数学的应用价值. 2.经历“问题——数学建模——问题解决”的过程,培养分析,解决问题的能力. 3.放手学生从多角度地了解勾股定理. 4.增强学生的动手能力. 5.学会运用勾股定理来解决一些实际问题,体会数学的应用价值. 6.尽可能的给学生提供机会展示他们查阅有关的勾股定理,进行交流,并在与他人交流的过程中敢于发表不同的见解,在交流活动中获得成功的体验.
教学重点、 难点 教学重点:应用勾股定理有关知识解决有关问题. 教学难点:灵活应用勾股定理有关知识解决有关问题.
教学准备 多媒体课件、三角尺
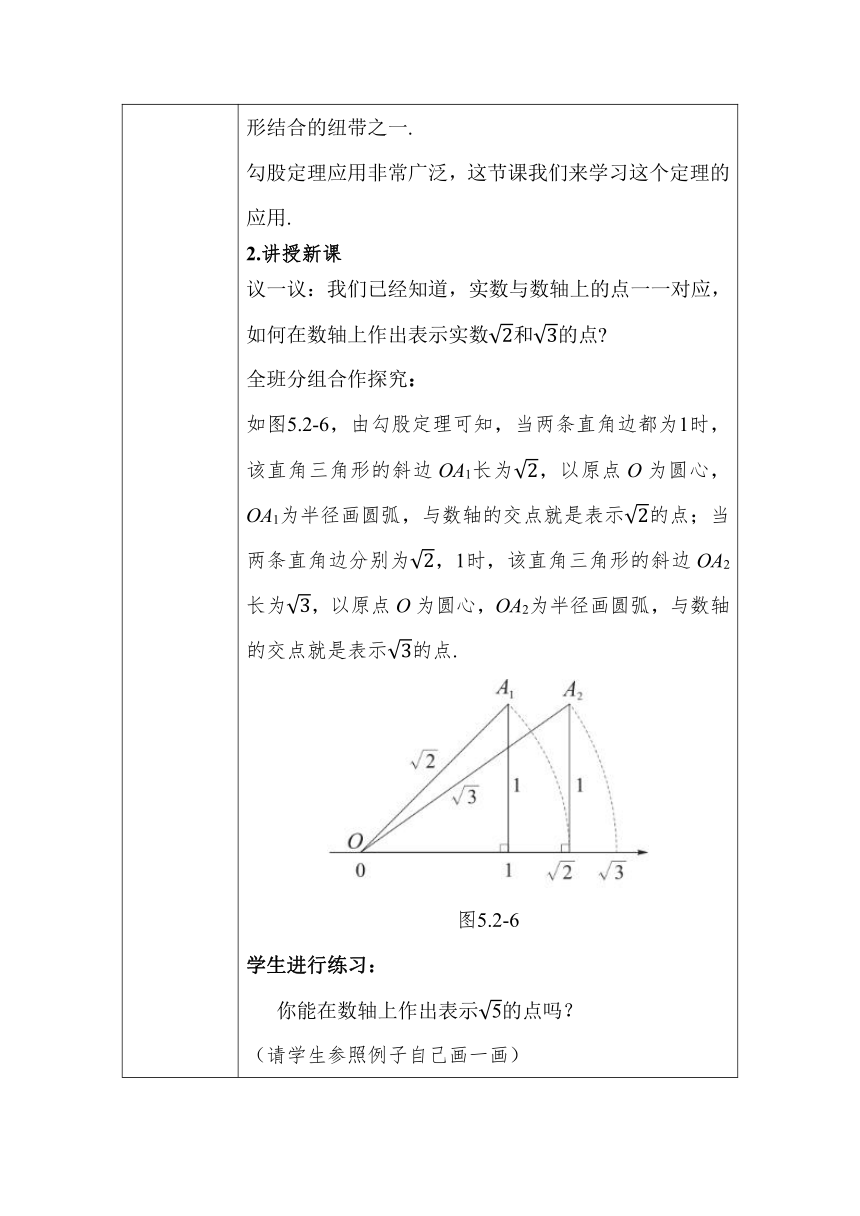
教学过程 1.情境导入 勾股定理的内容是什么? 如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. 勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一. 勾股定理应用非常广泛,这节课我们来学习这个定理的应用. 2.讲授新课 议一议:我们已经知道,实数与数轴上的点一一对应,如何在数轴上作出表示实数和的点 全班分组合作探究: 如图5.2-6,由勾股定理可知,当两条直角边都为1时,该直角三角形的斜边OA1长为,以原点O为圆心,OA1为半径画圆弧,与数轴的交点就是表示的点;当两条直角边分别为,1时,该直角三角形的斜边OA2长为,以原点O为圆心,OA2为半径画圆弧,与数轴的交点就是表示的点. 图5.2-6 学生进行练习: 你能在数轴上作出表示的点吗? (请学生参照例子自己画一画) 思考:图5.2-7是一位电工师傅准备利用梯子在墙上安装电灯的示意图.假设梯子长4 m,他将梯子靠在墙上,此时梯脚离墙脚的距离为1.5 m.他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近了0.5 m,那么,梯子顶端是否也上移0.5 m (已知≈3.71,≈3.87) 图5.2-7 根据已知条件可抽象出示意图5.2-8,分别在Rt△ABC和Rt△A'BC'中,运用勾股定理计算出AB,A'B,则可得出梯子顶端往上移动的距离. 图5.2-8 在Rt△ABC中,AC=4 m,BC=1.5 m, 于是,AB==≈3.71(m). 在Rt△A'BC'中,A'C'=4 m,BC'=1 m, 由勾股定理得,A'B==≈3.87(m), 因此A'A=A'B - AB≈3.87-3.71=0.16(m). 即梯子顶端A点大约向上移动了0.16 m,而不是向上移动0.5 m. 例3:(古代数学问题)“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何?”意思是:有一个池塘,其水面是边长为10尺的正方形,一棵芦苇生长在池的中央,其出水部分为1尺,如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面.问水深与芦苇长各为多少 分析 根据题意,先画出水池截面示意图,如图5.2-9所示.设AB为芦苇,BC为芦苇出水部分,长1尺,将芦苇拉向岸边,其顶部B点恰好碰到岸边B'. 图5.2-9 解:如图5.2-9,设水深x尺,则AC=x尺, AB=AB'=(x+1)尺. 因为池塘的水面是边长为10尺的正方形, 所以B'C=5尺. 在Rt△ACB'中,根据勾股定理得, x2+52=(x+1)2, 解得 x=12. 故芦苇长为13尺. 答:水深为12尺,芦苇长为13尺. 练习:如图,校园内有两棵树,相距12 m,一棵树高16m,另一棵树高11 m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米? 解:由题意有BC=12 m,AC=16-11=5(m). 在Rt△ABC中,AB===13(m). 答:小鸟至少要飞13 m. 3.课堂练习 1.如图,铁路和公路PQ在点O处交汇,∠QON= 30°.公路PQ上A处距O点240 m,如果火车行驶时,周围200 m以内会受到噪音的影响,那么火车在铁路上沿O方向以72 km/h的速度行驶时,A处受噪音影响的时间为________. 解析:如图,过点A作AC⊥ON,AB=AD=200 m. 因为∠QON=30°,OA=240 m,所以AC=120 m. 当火车到B点时对处产生噪音影响,此时AB=200 m. 因为AB=200 m,AC=120 m, 由勾股定理得BC=160 m,CD=160 m,即BD=320 m. 因为72 km/h=20 m/s, 所以影响时间应是320÷20=16(s). 方法总结:作辅助线构造直角三角形,再利用勾股定理是解这类题的关键. 2.由于过度采伐森林和破坏植被,我国许多地区频频遭受沙尘暴的侵袭,今日A市测得沙尘暴中心在A市的正西方向300 km的B处,以10 km/h的速度向南偏东60°的BF方向移动,距沙尘暴中心200 km的范围是受沙尘暴影响的区域,问:A市是否会受到沙尘暴的影响?若不会,说明理由;若会,求出A市受沙尘暴影响的时间. 解:如图,过点A作AC⊥BF于C,由题意得∠ABC= 90°-60°=30°,所以AC=AB=×300=150(km). 因为150<200,所以A市受沙尘暴影响,设从D点开始受影响,则AD=200 km. 由勾股定理得,CD===50(km),所以受影响的距离为2CD=100 km,受影响的时间位100÷10=10(h). 方法总结:熟记“直角三角形30°角所对的直角边等于斜边的一半”这一性质,知道方向角如何在图上表示,作辅助线构造直角三角形,再利用勾股定理是解这类题的关键. 3.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,则AM的长是( ) A.1.5 B.2 C.2.25 D.2.5 解析:设AM=x,连接BM,MB′, 在Rt△ABM中,AB2+AM2=BM2, 在Rt△MDB′中,B′M2=MD2+DB′2, 因为MB=MB′,所以AB2+AM2=BM2=B′M2=MD2+DB′2, 即92+x2=(9-x)2+(9-3))2,解得x=2,即AM=2. 故选B. 方法总结:解题的关键是设出适当的线段的长度为x,然后用含有x的式子表示其他线段,然后在直角三角形中利用勾股定理列方程解答. 4.课堂小结 1.勾股定理的实际应用 步骤:1.画出图形.2.明确已知量和未知量之间的关系.3.适当的设元,将几何问题转化为代数问题求解. 解题策略:对于非直角三角形问题,可通过作垂线构造直角三角形求解. 2.直角三角形应用的几种常见类型 5.板书设计 1.勾股定理在实际生活中的应用 2.勾股定理在几何图形中的应用
教学设计 反思 就练习的情况来看,一方面学生简单机械地套用了“a2+b2=c2”,没有分析问题的本质所在;另一方面对于立体图形转化为平面问题在实际问题中抽象出数学模型还存在较大的困难,在今后的教学中要通过实例不断训练提高.
授课教师 授课类型 新授课
教学目标 1.会用勾股定理来解决一些实际问题,体会数学的应用价值. 2.经历“问题——数学建模——问题解决”的过程,培养分析,解决问题的能力. 3.放手学生从多角度地了解勾股定理. 4.增强学生的动手能力. 5.学会运用勾股定理来解决一些实际问题,体会数学的应用价值. 6.尽可能的给学生提供机会展示他们查阅有关的勾股定理,进行交流,并在与他人交流的过程中敢于发表不同的见解,在交流活动中获得成功的体验.
教学重点、 难点 教学重点:应用勾股定理有关知识解决有关问题. 教学难点:灵活应用勾股定理有关知识解决有关问题.
教学准备 多媒体课件、三角尺
教学过程 1.情境导入 勾股定理的内容是什么? 如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2. 勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一. 勾股定理应用非常广泛,这节课我们来学习这个定理的应用. 2.讲授新课 议一议:我们已经知道,实数与数轴上的点一一对应,如何在数轴上作出表示实数和的点 全班分组合作探究: 如图5.2-6,由勾股定理可知,当两条直角边都为1时,该直角三角形的斜边OA1长为,以原点O为圆心,OA1为半径画圆弧,与数轴的交点就是表示的点;当两条直角边分别为,1时,该直角三角形的斜边OA2长为,以原点O为圆心,OA2为半径画圆弧,与数轴的交点就是表示的点. 图5.2-6 学生进行练习: 你能在数轴上作出表示的点吗? (请学生参照例子自己画一画) 思考:图5.2-7是一位电工师傅准备利用梯子在墙上安装电灯的示意图.假设梯子长4 m,他将梯子靠在墙上,此时梯脚离墙脚的距离为1.5 m.他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近了0.5 m,那么,梯子顶端是否也上移0.5 m (已知≈3.71,≈3.87) 图5.2-7 根据已知条件可抽象出示意图5.2-8,分别在Rt△ABC和Rt△A'BC'中,运用勾股定理计算出AB,A'B,则可得出梯子顶端往上移动的距离. 图5.2-8 在Rt△ABC中,AC=4 m,BC=1.5 m, 于是,AB==≈3.71(m). 在Rt△A'BC'中,A'C'=4 m,BC'=1 m, 由勾股定理得,A'B==≈3.87(m), 因此A'A=A'B - AB≈3.87-3.71=0.16(m). 即梯子顶端A点大约向上移动了0.16 m,而不是向上移动0.5 m. 例3:(古代数学问题)“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何?”意思是:有一个池塘,其水面是边长为10尺的正方形,一棵芦苇生长在池的中央,其出水部分为1尺,如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面.问水深与芦苇长各为多少 分析 根据题意,先画出水池截面示意图,如图5.2-9所示.设AB为芦苇,BC为芦苇出水部分,长1尺,将芦苇拉向岸边,其顶部B点恰好碰到岸边B'. 图5.2-9 解:如图5.2-9,设水深x尺,则AC=x尺, AB=AB'=(x+1)尺. 因为池塘的水面是边长为10尺的正方形, 所以B'C=5尺. 在Rt△ACB'中,根据勾股定理得, x2+52=(x+1)2, 解得 x=12. 故芦苇长为13尺. 答:水深为12尺,芦苇长为13尺. 练习:如图,校园内有两棵树,相距12 m,一棵树高16m,另一棵树高11 m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米? 解:由题意有BC=12 m,AC=16-11=5(m). 在Rt△ABC中,AB===13(m). 答:小鸟至少要飞13 m. 3.课堂练习 1.如图,铁路和公路PQ在点O处交汇,∠QON= 30°.公路PQ上A处距O点240 m,如果火车行驶时,周围200 m以内会受到噪音的影响,那么火车在铁路上沿O方向以72 km/h的速度行驶时,A处受噪音影响的时间为________. 解析:如图,过点A作AC⊥ON,AB=AD=200 m. 因为∠QON=30°,OA=240 m,所以AC=120 m. 当火车到B点时对处产生噪音影响,此时AB=200 m. 因为AB=200 m,AC=120 m, 由勾股定理得BC=160 m,CD=160 m,即BD=320 m. 因为72 km/h=20 m/s, 所以影响时间应是320÷20=16(s). 方法总结:作辅助线构造直角三角形,再利用勾股定理是解这类题的关键. 2.由于过度采伐森林和破坏植被,我国许多地区频频遭受沙尘暴的侵袭,今日A市测得沙尘暴中心在A市的正西方向300 km的B处,以10 km/h的速度向南偏东60°的BF方向移动,距沙尘暴中心200 km的范围是受沙尘暴影响的区域,问:A市是否会受到沙尘暴的影响?若不会,说明理由;若会,求出A市受沙尘暴影响的时间. 解:如图,过点A作AC⊥BF于C,由题意得∠ABC= 90°-60°=30°,所以AC=AB=×300=150(km). 因为150<200,所以A市受沙尘暴影响,设从D点开始受影响,则AD=200 km. 由勾股定理得,CD===50(km),所以受影响的距离为2CD=100 km,受影响的时间位100÷10=10(h). 方法总结:熟记“直角三角形30°角所对的直角边等于斜边的一半”这一性质,知道方向角如何在图上表示,作辅助线构造直角三角形,再利用勾股定理是解这类题的关键. 3.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,则AM的长是( ) A.1.5 B.2 C.2.25 D.2.5 解析:设AM=x,连接BM,MB′, 在Rt△ABM中,AB2+AM2=BM2, 在Rt△MDB′中,B′M2=MD2+DB′2, 因为MB=MB′,所以AB2+AM2=BM2=B′M2=MD2+DB′2, 即92+x2=(9-x)2+(9-3))2,解得x=2,即AM=2. 故选B. 方法总结:解题的关键是设出适当的线段的长度为x,然后用含有x的式子表示其他线段,然后在直角三角形中利用勾股定理列方程解答. 4.课堂小结 1.勾股定理的实际应用 步骤:1.画出图形.2.明确已知量和未知量之间的关系.3.适当的设元,将几何问题转化为代数问题求解. 解题策略:对于非直角三角形问题,可通过作垂线构造直角三角形求解. 2.直角三角形应用的几种常见类型 5.板书设计 1.勾股定理在实际生活中的应用 2.勾股定理在几何图形中的应用
教学设计 反思 就练习的情况来看,一方面学生简单机械地套用了“a2+b2=c2”,没有分析问题的本质所在;另一方面对于立体图形转化为平面问题在实际问题中抽象出数学模型还存在较大的困难,在今后的教学中要通过实例不断训练提高.
同课章节目录
