2.1 从小学算术说起 课件(共28张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册
文档属性
| 名称 | 2.1 从小学算术说起 课件(共28张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
第二章 有理数及其运算
六年级上册
1 从小学算术说起
课前小测
A
2000+3=2003(m)
a×(b+c) =ab+ac
1.如图所示,竖式中圈起来的进位“1”表示( )
A.1个百 B.1个十 C.1个一
2.请你把2km加3m写成一个算式的形式:
如: 等。
3.请用字母表示乘法对加法的分配律:
。
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在小学,你还记得学习了哪些数学运算方面的知识?
整数的四则运算
小数的四则运算
分数的四则运算
约分,通分
运算律
……
新知初探
贰
合作探究
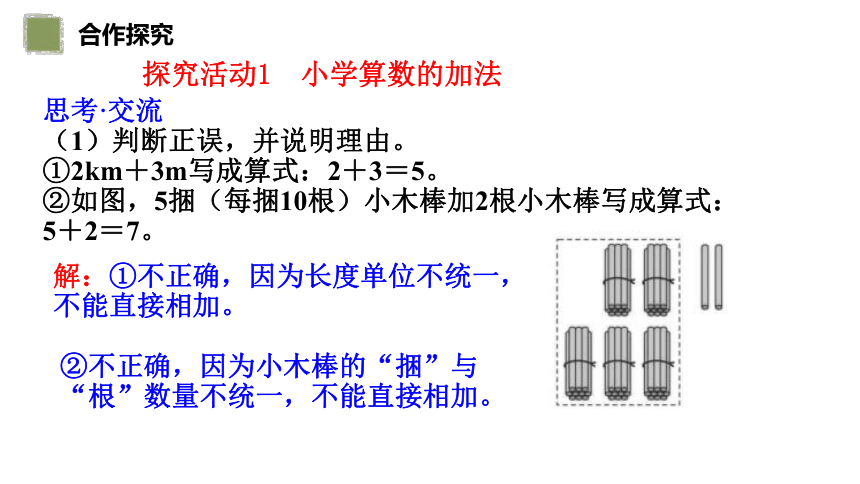
探究活动1 小学算数的加法
思考·交流
(1)判断正误,并说明理由。
①2km+3m写成算式:2+3=5。
②如图,5捆(每捆10根)小木棒加2根小木棒写成算式:5+2=7。
解:①不正确,因为长度单位不统一,不能直接相加。
②不正确,因为小木棒的“捆”与“根”数量不统一,不能直接相加。
合作探究
(2)如图,2.34+2.1写成竖式的形式,为什么要求“小数点对齐,相同数位上的数相加”?
不同数位上的数相加是错误的,只有计数单位相同的才能相加减。
不成立,同分母分数相加减,分母不变,把分子相加减。异分母分数相加减则要先通分化为同分母的分数后相加减,不能直接把分子相加作分子、分母相加作分母。
(3) 成立吗?两个分数相加,为什么不能用分子的和作为和的分子,分母的和作为和的分母?
归纳小结
1.加法的意义:把两个数合并成一个数的运算.
2.加法运算:
(1)整数、小数的加法:相同数位上的数字对齐(对于小数来说,要把小数点对齐),从低位算起,哪一位上的数相加满十,向前一位进一.
(2)分数的加法:①同分母分数相加,分母不变,分子相加;
②异分母分数相加,先通分,然后按照同分母分数相加的法则进行计算.
典例分析
例1 计算:
解:(1)8+11=19;
(2)0.618+3.14=3.758;
归纳小结
(1)对于加法运算,要记三条:①相同数位对齐;②从低位加起;③满十进一,三者缺一不可。
(2)对于涉及实际意义的加法,还要注意单位一致,如8g加11kg不能写成算式:8+11=19。
(3)对于带分数的加法,可先化成假分数再计算,也可通过拆分,把整数部分与分数部分分别相加。
合作探究
探究活动2 运算律
尝试·思考
怎样计算更简便?理论依据是什么?
合作探究
探究活动2 运算律
观察·思考
(1)把两个长方形拼成如图所示的一个长方形。
口答:75×9= 。
675
(2)如图是一个999×1000的长方形。
口答:999×999= 。
(3)把两个长方形拼成如图所示的一个长方形。若a=67,b=33,m=56,则
56×67+56×33= 。
998001
5600
75×9=(70+5)×9=70×9+5×9=630+45=675。
999×999=(1000-1)×999=999000-999=998001。
56×67+56×33=56×(67+33)=56×100=5600。
归纳小结
(1)加法交换律:a+b=b+a;
(2)加法结合律:(a+b)+c=a+(b+c);
(3)乘法交换律:a×b=b×a;
(4)乘法结合律:(a×b)×c=a×(b×c);
(5)乘法对加法的分配律:a×(b+c)=ab+ac.
尝试·思考
已知a与b都是自然数,a+b,a-b,a×b也都是自然数吗?
a+b,a×b也都是自然数,a-b,a÷b不一定是自然数。
典例分析
计算:
例2
归纳小结
(1)在进行运算之前,应考虑是把分数化为小数,还是把小数化为分数.如果分数能够化为有限小数,那么化为小数运算比较简便;如果分数不能化为有限小数,一般将小数化为分数运算。
(2)在计算之前,要考虑运算顺序,即先算什么,再算什么.
(3)计算时,要认真审题,看清运算符号和数的特点,灵活选择合理的计算方法,数学中的运算性质和运算律在这方面有较大的作用.通常在分数的计算中,两个分数相加、减时,能“凑整”的可以先算.可用分配律使分母简化的则用分配律计算.乘法中可用交换律的则先用交换律.总之,要根据题中具体数字来考虑如何使运算过程简便,要能运用各种运算律来进行计算.
合作探究
探究活动3 表达具有相反意义的量
( 1 )小丽从小养成了理财的习惯。上个月她卖了一次废品,并给自己
买了一本课外书。她在账本上记录: +56.2元,-27.5元。试说明“+56.2元”“-27.5元"的实际意义。
(2)生活中会发生可以写成算式“2-3” 的故事。例如,某地现在的气温是2 ℃,后下降了3℃。试讲一个“2-3”的故事。
尝试·交流
解:(1)“+56.2元”表示上个月小丽卖了一次废品收入56.2元;“-27.5元”表示小丽给自己买了一本课外书支出27.5元。
(2)答案不唯一,如张先生某月收入2万元,支出3万元,则他该月的收支情况可表示为“2-3”。
归纳小结
1.正数、负数的意义
像3,1.8%,3.5这样大于0的数叫作正数,像-3,-1.8%,-3.5这样在正数前加上符号“一”(负)的数叫作负数.为了明确表达意义,在正数前面也加上“+”(正)号.
2.表达具有相反意义的量
为了表示具有相反意义的量,我们可把其中一个量规定为正的,用正数来表示,而把与这个量意义相反的量规定为负的,用负数来表示。
典例分析
例3(1)若一个乒乓球超出标准质量5 mg记作+5 mg,则恰好为标准质量应记作 ,低于标准质量3 mg应记作 ;
(2)某中学举行了一次党史知识竞赛,规定答对一题记10分,不答记0分,则-10分表示 。
0 mg
-3 mg
答错一道题
温馨提示
注意相反意义的量与反义词的区别,如上升与下降虽然意义相反,但缺少数量,因此并不是相反意义的量。相反意义的量中的两个量必须是同类量,如节约3吨汽油与浪费1吨水就不是具有相反意义的量。
当堂达标
叁
当堂达标
C
A.乘法交换律及乘法结合律
B.乘法交换律及乘法对加法的分配律
C.乘法结合律及乘法对加法的分配律
D.乘法对加法的分配律及加法结合律
1.式子4×25×( )=100×( )=50-30+
40中用的运算律是( )
当堂达标
2. 纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京晚的时数):
当北京6月15日23时,悉尼、纽约的时间发别是( )
A.6月16日1时;6月15日10时 B.6月16日1时;6月14日10时
C.6月15日21时;6月15日10时 D.6月15日21时;6月16日12时
解析:悉尼的时间:6月15日23时+2小时=6月15日1时;
纽约的时间:6月15日23时-13小时=6月15日10时。
A
当堂达标
3.
当堂达标
4.判断下列计算是否正确,并说明理由。
原式乘分母2与3的最小公倍数6,再乘六分之一,这样不改变原算式结果的大小,然后就可利用乘法的结合律与分配律进行简便运算。
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
转化思想
数形结合思想
作业布置
详见教材习题
P30 T1-5
谢
谢
第二章 有理数及其运算
六年级上册
1 从小学算术说起
课前小测
A
2000+3=2003(m)
a×(b+c) =ab+ac
1.如图所示,竖式中圈起来的进位“1”表示( )
A.1个百 B.1个十 C.1个一
2.请你把2km加3m写成一个算式的形式:
如: 等。
3.请用字母表示乘法对加法的分配律:
。
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在小学,你还记得学习了哪些数学运算方面的知识?
整数的四则运算
小数的四则运算
分数的四则运算
约分,通分
运算律
……
新知初探
贰
合作探究
探究活动1 小学算数的加法
思考·交流
(1)判断正误,并说明理由。
①2km+3m写成算式:2+3=5。
②如图,5捆(每捆10根)小木棒加2根小木棒写成算式:5+2=7。
解:①不正确,因为长度单位不统一,不能直接相加。
②不正确,因为小木棒的“捆”与“根”数量不统一,不能直接相加。
合作探究
(2)如图,2.34+2.1写成竖式的形式,为什么要求“小数点对齐,相同数位上的数相加”?
不同数位上的数相加是错误的,只有计数单位相同的才能相加减。
不成立,同分母分数相加减,分母不变,把分子相加减。异分母分数相加减则要先通分化为同分母的分数后相加减,不能直接把分子相加作分子、分母相加作分母。
(3) 成立吗?两个分数相加,为什么不能用分子的和作为和的分子,分母的和作为和的分母?
归纳小结
1.加法的意义:把两个数合并成一个数的运算.
2.加法运算:
(1)整数、小数的加法:相同数位上的数字对齐(对于小数来说,要把小数点对齐),从低位算起,哪一位上的数相加满十,向前一位进一.
(2)分数的加法:①同分母分数相加,分母不变,分子相加;
②异分母分数相加,先通分,然后按照同分母分数相加的法则进行计算.
典例分析
例1 计算:
解:(1)8+11=19;
(2)0.618+3.14=3.758;
归纳小结
(1)对于加法运算,要记三条:①相同数位对齐;②从低位加起;③满十进一,三者缺一不可。
(2)对于涉及实际意义的加法,还要注意单位一致,如8g加11kg不能写成算式:8+11=19。
(3)对于带分数的加法,可先化成假分数再计算,也可通过拆分,把整数部分与分数部分分别相加。
合作探究
探究活动2 运算律
尝试·思考
怎样计算更简便?理论依据是什么?
合作探究
探究活动2 运算律
观察·思考
(1)把两个长方形拼成如图所示的一个长方形。
口答:75×9= 。
675
(2)如图是一个999×1000的长方形。
口答:999×999= 。
(3)把两个长方形拼成如图所示的一个长方形。若a=67,b=33,m=56,则
56×67+56×33= 。
998001
5600
75×9=(70+5)×9=70×9+5×9=630+45=675。
999×999=(1000-1)×999=999000-999=998001。
56×67+56×33=56×(67+33)=56×100=5600。
归纳小结
(1)加法交换律:a+b=b+a;
(2)加法结合律:(a+b)+c=a+(b+c);
(3)乘法交换律:a×b=b×a;
(4)乘法结合律:(a×b)×c=a×(b×c);
(5)乘法对加法的分配律:a×(b+c)=ab+ac.
尝试·思考
已知a与b都是自然数,a+b,a-b,a×b也都是自然数吗?
a+b,a×b也都是自然数,a-b,a÷b不一定是自然数。
典例分析
计算:
例2
归纳小结
(1)在进行运算之前,应考虑是把分数化为小数,还是把小数化为分数.如果分数能够化为有限小数,那么化为小数运算比较简便;如果分数不能化为有限小数,一般将小数化为分数运算。
(2)在计算之前,要考虑运算顺序,即先算什么,再算什么.
(3)计算时,要认真审题,看清运算符号和数的特点,灵活选择合理的计算方法,数学中的运算性质和运算律在这方面有较大的作用.通常在分数的计算中,两个分数相加、减时,能“凑整”的可以先算.可用分配律使分母简化的则用分配律计算.乘法中可用交换律的则先用交换律.总之,要根据题中具体数字来考虑如何使运算过程简便,要能运用各种运算律来进行计算.
合作探究
探究活动3 表达具有相反意义的量
( 1 )小丽从小养成了理财的习惯。上个月她卖了一次废品,并给自己
买了一本课外书。她在账本上记录: +56.2元,-27.5元。试说明“+56.2元”“-27.5元"的实际意义。
(2)生活中会发生可以写成算式“2-3” 的故事。例如,某地现在的气温是2 ℃,后下降了3℃。试讲一个“2-3”的故事。
尝试·交流
解:(1)“+56.2元”表示上个月小丽卖了一次废品收入56.2元;“-27.5元”表示小丽给自己买了一本课外书支出27.5元。
(2)答案不唯一,如张先生某月收入2万元,支出3万元,则他该月的收支情况可表示为“2-3”。
归纳小结
1.正数、负数的意义
像3,1.8%,3.5这样大于0的数叫作正数,像-3,-1.8%,-3.5这样在正数前加上符号“一”(负)的数叫作负数.为了明确表达意义,在正数前面也加上“+”(正)号.
2.表达具有相反意义的量
为了表示具有相反意义的量,我们可把其中一个量规定为正的,用正数来表示,而把与这个量意义相反的量规定为负的,用负数来表示。
典例分析
例3(1)若一个乒乓球超出标准质量5 mg记作+5 mg,则恰好为标准质量应记作 ,低于标准质量3 mg应记作 ;
(2)某中学举行了一次党史知识竞赛,规定答对一题记10分,不答记0分,则-10分表示 。
0 mg
-3 mg
答错一道题
温馨提示
注意相反意义的量与反义词的区别,如上升与下降虽然意义相反,但缺少数量,因此并不是相反意义的量。相反意义的量中的两个量必须是同类量,如节约3吨汽油与浪费1吨水就不是具有相反意义的量。
当堂达标
叁
当堂达标
C
A.乘法交换律及乘法结合律
B.乘法交换律及乘法对加法的分配律
C.乘法结合律及乘法对加法的分配律
D.乘法对加法的分配律及加法结合律
1.式子4×25×( )=100×( )=50-30+
40中用的运算律是( )
当堂达标
2. 纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京晚的时数):
当北京6月15日23时,悉尼、纽约的时间发别是( )
A.6月16日1时;6月15日10时 B.6月16日1时;6月14日10时
C.6月15日21时;6月15日10时 D.6月15日21时;6月16日12时
解析:悉尼的时间:6月15日23时+2小时=6月15日1时;
纽约的时间:6月15日23时-13小时=6月15日10时。
A
当堂达标
3.
当堂达标
4.判断下列计算是否正确,并说明理由。
原式乘分母2与3的最小公倍数6,再乘六分之一,这样不改变原算式结果的大小,然后就可利用乘法的结合律与分配律进行简便运算。
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
转化思想
数形结合思想
作业布置
详见教材习题
P30 T1-5
谢
谢
同课章节目录
