2.2第1课时 有理数 课件(共25张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册
文档属性
| 名称 | 2.2第1课时 有理数 课件(共25张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:06:36 | ||
图片预览








文档简介
(共25张PPT)
第二章 有理数及其运算
六年级上册
认识有理数
第1课时 有理数
2.下列四个数中,是自然数的是( )
A.﹣1 B.0 C. D.2.1
课前小测
B
1. 月球表面的白天平均温度零上126 ℃记作+126 ℃,夜间平均温度零下150 ℃应记作( )
A.+150 ℃ B.﹣150 ℃
C.+276 ℃ D.﹣276 ℃
B
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
同学们小学都学过哪些数
整数、小数、分数、奇数、偶数……
原始社会,从打猎记数开始,首先出现自然数,经过漫长岁月,人们用数“0”表示没有,随着人类的不断进步,在丈量土地进行分配时,又用小数使测量结果更加准确,小数也属于分数.那么小学学过的这些数能否满足社会生产生活及数学自身发展的需要呢
新知初探
贰
合作探究
探究活动1 正数与负数的意义
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分;每个参赛队的基本分均为0分。两个队答题情况如下表:
如果答对题所得的分数用正数表示,那么你能写出每个队答题得分的情况吗
合作探究
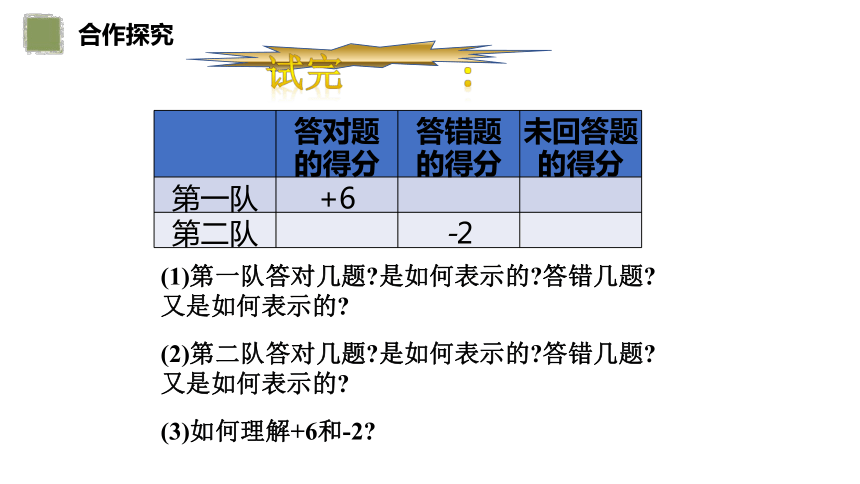
试完成下表:
答对题 的得分 答错题 的得分
未回答题
的得分
第一队 +6
第二队 -2
(1)第一队答对几题 是如何表示的 答错几题 又是如何表示的
(2)第二队答对几题 是如何表示的 答错几题 又是如何表示的
(3)如何理解+6和-2
合作探究
尝试·交流
(1)下表是某日四个城市的气温情况。你能说出表中各数的实际意义吗?
(2)珠穆朗玛峰的海拔大约是8 848.86 m,吐鲁番盆地最低处的海拔大约是-154.31 m。8 848.86 m, -154.31 m两数的实际意义分别是什么
(3)课本图2-7展示了2023年7月我国居民消费价格分类别同比涨跌情况。请你说一说-0.5%,2.4% 等数的实际意义,并与同伴进行交流。
归纳小结
(1)为了表示具有相反意义的量,我们可以把其中的一个量规定为正的,把与这个量意义相反的量规定为负的,并分别用“+”“-”来表示。
(2)像+3,+15,+2.4%,…都是正数,像-2,-8,-0.5%,…都是负数。0既不是正数,也不是负数。
“+”读作“正”,如“+3”读作“正3”,正号“+”通常省略不写“-”读作“负”, 如“-8”读作“负8”。
(3)负数与对应的正数在数量上相等,表示的意义相反。
温馨提示:(1)比0大的数为正数,比0小的数为负数。
(2)判断一个数是正数还是负数,不能简单地认为带有“+”号的数就是正数,带有“-”号的数就是负数.如+(-3)就不是正数,-(-3)也不是负数,在今后的学习中将进一步研究它们。
典例分析
例1 (1)某人转动转盘,如果用+5表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示
(2)在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02 g记作+0.02 g,那么-0.03 g表示什么
(3)某大米包装袋上标注着“净含量:10 kg±150 g”,这里的“10 kg±50 g”表示什么
解:(1)沿顺时针方向转了12圈记作-12圈;
(2)-0.03 g表示乒乓球的质量低于标准质量0.03g;
(3)每袋大米的标准质量应为10kg,但实际每袋大米可能有50g的误差,即每袋大米的净含量最多是10kg+50g,最少是10kg-50g。
归纳小结
正数和负数可以用来表示日常生活中具有相反意义的量,零则是正数与负数的分界,是“基准”,具有“初始位置”的含义,注意0的意义不仅仅是表示没有。在用正数和负数表示具有相反意义的量时,哪种意义为正,是可以任意选择的,我们习惯上把“前进、上升、收入”等规定为正,而把“后退、下降、支出”等规定为负。
合作探究
探究活动2 有理数的意义及分类
思考·交流
(1)选定一个身体高度作为标准,用正负数和0表示班内每名同学的身高与选定的身高标准的差。你是怎样表示的?从你的表示中能看出谁最高吗?
(2)你能将学过的数进行分类吗?与同伴进行交流。
归纳小结
1. 、 、 统称为整数;
、 统称为分数。
2. 和 统称为有理数。
正整数
0
负整数
正分数
负分数
整数
分数
3.有理数的分类
典例分析
正数集合{ …};
负数集合{ …};
正整数集合{ …};
负整数集合{ …};
分数集合{ …};
负分数集合{ …};
负有理数集合{ …};
有理数集合{ …}.
将下列各数填入到相应的数集中:
归纳小结
(1)解这类问题关键在于两点:一是明确各类数的含义与分类;二是按一定顺序认真查找,做到不重不漏.另外,正数与整数是两个不同的概念,分数与小数并不等同,注意不要混淆。
(2)有理数只包括整数和分数,同时结合小学时对数的认识,可知分数包括有限小数与无限循环小数,无限不循环小数不能化为分数,所以不是有理数,如圆周率的值π就不是有理数,特别注意,不要误认为 是分数。
当堂达标
叁
1.[跨学科—音乐]如图是某古筝调音器软件的界面,已知古筝是标准音时,界面指针指向0,指针指向40表示音调偏高,需放松琴弦。当古筝的音调低于标准音30时,该界面指针指向的数字是( )
当堂达标
B
A.-40 B.-30
C.0 D.30
当堂达标
2.在0,2,-7, ,3.14, ,-3,+0.75中,
负数共有 ( )
A.1个 B.2个 C.3个 D.4个
解析:在正数的前面加上“-”号的数即是负数,本题中的-7, , ,-3是负数.故选D.
D
当堂达标
3.下列说法:①-一个有理数不是正数就是负数;②一个有理数不是整数就是分数;③0既不是正数也不是负数;④0是最小的自然数;⑤0是最小的整数;⑥0既不是奇数,也不是偶数;⑦0是最小的非负数;⑧自然数就是正整数。其中正确的有( )
A.4个 B.5个 C.6个 D.7个
A
当堂达标
4.举一个能用正数、负数表示生活中的量的实例,并解释其中相关数量的含义.
解: 本题答案不唯一,只要满足题意即可,如:河道中第一天的水位是-0.2米,第二天的水位是+0.3米,其中-0.2米表示比正常水位低0.2米,+0.3米表示比正常水位高0.3米.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
作业布置
详见教材习题
P35 T1-6
谢
谢
第二章 有理数及其运算
六年级上册
认识有理数
第1课时 有理数
2.下列四个数中,是自然数的是( )
A.﹣1 B.0 C. D.2.1
课前小测
B
1. 月球表面的白天平均温度零上126 ℃记作+126 ℃,夜间平均温度零下150 ℃应记作( )
A.+150 ℃ B.﹣150 ℃
C.+276 ℃ D.﹣276 ℃
B
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
同学们小学都学过哪些数
整数、小数、分数、奇数、偶数……
原始社会,从打猎记数开始,首先出现自然数,经过漫长岁月,人们用数“0”表示没有,随着人类的不断进步,在丈量土地进行分配时,又用小数使测量结果更加准确,小数也属于分数.那么小学学过的这些数能否满足社会生产生活及数学自身发展的需要呢
新知初探
贰
合作探究
探究活动1 正数与负数的意义
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分;每个参赛队的基本分均为0分。两个队答题情况如下表:
如果答对题所得的分数用正数表示,那么你能写出每个队答题得分的情况吗
合作探究
试完成下表:
答对题 的得分 答错题 的得分
未回答题
的得分
第一队 +6
第二队 -2
(1)第一队答对几题 是如何表示的 答错几题 又是如何表示的
(2)第二队答对几题 是如何表示的 答错几题 又是如何表示的
(3)如何理解+6和-2
合作探究
尝试·交流
(1)下表是某日四个城市的气温情况。你能说出表中各数的实际意义吗?
(2)珠穆朗玛峰的海拔大约是8 848.86 m,吐鲁番盆地最低处的海拔大约是-154.31 m。8 848.86 m, -154.31 m两数的实际意义分别是什么
(3)课本图2-7展示了2023年7月我国居民消费价格分类别同比涨跌情况。请你说一说-0.5%,2.4% 等数的实际意义,并与同伴进行交流。
归纳小结
(1)为了表示具有相反意义的量,我们可以把其中的一个量规定为正的,把与这个量意义相反的量规定为负的,并分别用“+”“-”来表示。
(2)像+3,+15,+2.4%,…都是正数,像-2,-8,-0.5%,…都是负数。0既不是正数,也不是负数。
“+”读作“正”,如“+3”读作“正3”,正号“+”通常省略不写“-”读作“负”, 如“-8”读作“负8”。
(3)负数与对应的正数在数量上相等,表示的意义相反。
温馨提示:(1)比0大的数为正数,比0小的数为负数。
(2)判断一个数是正数还是负数,不能简单地认为带有“+”号的数就是正数,带有“-”号的数就是负数.如+(-3)就不是正数,-(-3)也不是负数,在今后的学习中将进一步研究它们。
典例分析
例1 (1)某人转动转盘,如果用+5表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示
(2)在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02 g记作+0.02 g,那么-0.03 g表示什么
(3)某大米包装袋上标注着“净含量:10 kg±150 g”,这里的“10 kg±50 g”表示什么
解:(1)沿顺时针方向转了12圈记作-12圈;
(2)-0.03 g表示乒乓球的质量低于标准质量0.03g;
(3)每袋大米的标准质量应为10kg,但实际每袋大米可能有50g的误差,即每袋大米的净含量最多是10kg+50g,最少是10kg-50g。
归纳小结
正数和负数可以用来表示日常生活中具有相反意义的量,零则是正数与负数的分界,是“基准”,具有“初始位置”的含义,注意0的意义不仅仅是表示没有。在用正数和负数表示具有相反意义的量时,哪种意义为正,是可以任意选择的,我们习惯上把“前进、上升、收入”等规定为正,而把“后退、下降、支出”等规定为负。
合作探究
探究活动2 有理数的意义及分类
思考·交流
(1)选定一个身体高度作为标准,用正负数和0表示班内每名同学的身高与选定的身高标准的差。你是怎样表示的?从你的表示中能看出谁最高吗?
(2)你能将学过的数进行分类吗?与同伴进行交流。
归纳小结
1. 、 、 统称为整数;
、 统称为分数。
2. 和 统称为有理数。
正整数
0
负整数
正分数
负分数
整数
分数
3.有理数的分类
典例分析
正数集合{ …};
负数集合{ …};
正整数集合{ …};
负整数集合{ …};
分数集合{ …};
负分数集合{ …};
负有理数集合{ …};
有理数集合{ …}.
将下列各数填入到相应的数集中:
归纳小结
(1)解这类问题关键在于两点:一是明确各类数的含义与分类;二是按一定顺序认真查找,做到不重不漏.另外,正数与整数是两个不同的概念,分数与小数并不等同,注意不要混淆。
(2)有理数只包括整数和分数,同时结合小学时对数的认识,可知分数包括有限小数与无限循环小数,无限不循环小数不能化为分数,所以不是有理数,如圆周率的值π就不是有理数,特别注意,不要误认为 是分数。
当堂达标
叁
1.[跨学科—音乐]如图是某古筝调音器软件的界面,已知古筝是标准音时,界面指针指向0,指针指向40表示音调偏高,需放松琴弦。当古筝的音调低于标准音30时,该界面指针指向的数字是( )
当堂达标
B
A.-40 B.-30
C.0 D.30
当堂达标
2.在0,2,-7, ,3.14, ,-3,+0.75中,
负数共有 ( )
A.1个 B.2个 C.3个 D.4个
解析:在正数的前面加上“-”号的数即是负数,本题中的-7, , ,-3是负数.故选D.
D
当堂达标
3.下列说法:①-一个有理数不是正数就是负数;②一个有理数不是整数就是分数;③0既不是正数也不是负数;④0是最小的自然数;⑤0是最小的整数;⑥0既不是奇数,也不是偶数;⑦0是最小的非负数;⑧自然数就是正整数。其中正确的有( )
A.4个 B.5个 C.6个 D.7个
A
当堂达标
4.举一个能用正数、负数表示生活中的量的实例,并解释其中相关数量的含义.
解: 本题答案不唯一,只要满足题意即可,如:河道中第一天的水位是-0.2米,第二天的水位是+0.3米,其中-0.2米表示比正常水位低0.2米,+0.3米表示比正常水位高0.3米.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
作业布置
详见教材习题
P35 T1-6
谢
谢
同课章节目录
