2.2第2课时 数轴 课件(共26张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册
文档属性
| 名称 | 2.2第2课时 数轴 课件(共26张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:07:44 | ||
图片预览








文档简介
(共26张PPT)
第二章 有理数及其运算
六年级上册
2 认识有理数
第2课时 数轴
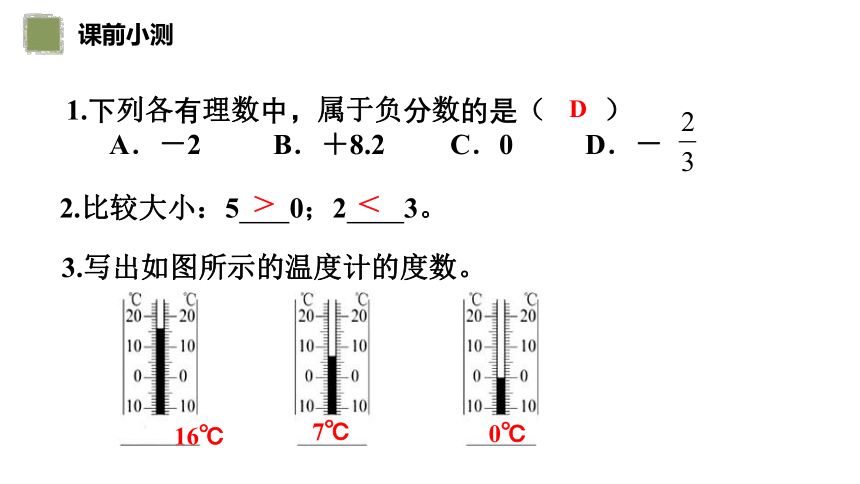
3.写出如图所示的温度计的度数。
课前小测
>
1.下列各有理数中,属于负分数的是( )
A.-2 B.+8.2 C.0 D.-
D
2.比较大小:5 0;2 3。
<
16℃
7℃
0℃
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在一条东西向的马路上,有一个汽车站,汽车站东3 m和7.5 m处分别有一棵柳树和一棵杨树,汽车站西3 m和4.8 m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
情境导入
(1)汽车站东3 m和西3 m分别表示什么意义
(2)汽车站处可以理解为温度计的什么点
请你尝试画图理解.
思考
新知初探
贰
合作探究
探究活动1 数轴的概念与画法
(1)图中温度计上显示的温度各是多少
(2)温度计上的刻度有什么特点
(3)如果把温度计看作是一条标有刻度的直线,那么你能用直线上的点表示有理数吗
合作探究
其实,一个平放的温度计可以看成一条数轴。
画数轴的步骤:
(1)画直线:画一条水平的直线;
(2)取原点:在直线上取一个适当的点作为原点,标上“0”;
(3)定方向:一般规定向右为正方向(画箭头表示);
(4)选长度:选取合适的长度作为单位长度;
(5)标读数:在原点右边标正数,在原点左边标负数。
归纳小结
1.规定了 、 和 的直线称为数轴。
温馨提示:数轴的定义包含三层含义:①数轴是一条直线,可以向两端无限延伸;②数轴有三要素:原点、正方向、单位长度,三者缺一不可;③原点位置的选定,单位长度的大小的确定,正方向的取向,都是根据实际需要“规定”的。同一数轴的单位长度要一致。
原点
单位长度
正方向
2.任何一个有理数都可以用数轴上的一个点来表示。
典例分析
例1 如图,数轴上点A,B,C分别表示什么数?
解: A点表示-2,B点表示2,C点表示0,D点表示-1。
典例分析
例2 画出数轴,并用数轴上的点表示下列各数: , -5, 0, 5, -4, 。
解:如图所示。
-5
0
-4
5
温馨提示:判断数轴画得是否正确,首先检查三要素是否齐全;其次还要注意检查单位长度是否一致,原点左右两边数的顺序是否正确。另外,注意数轴的两端都不能画点,防止把直线画成射线或线段。
合作探究
探究活动2 利用数轴比较有理数的大小
思考·交流
(2)①数轴上的两个点,右边点表示的数与左边点表示的数有怎样的大小关系
②正数、负数在数轴上的什么位置 判断它们的大小。
(1)我们把温度计按如图所示的方式放置,温度变化的规律是什么
归纳小结
有理数的大小比较方法:
(1)数轴上两个点表示的数,右边的总比左边的大。
(2)正数大于0,负数小于0,正数大于负数。
典例分析
例3 画出数轴,用数轴上的点表示下列各数,并用“<”将它们连接起来。
,﹣3.5,0,3,﹣4,﹣ 。
解:把各数表示在数轴上如图,
归纳小结
利用数轴比较有理数的大小的步骤:
(1)画数轴;
(2)表示点:在数轴上描出相应各点,确定各点在数轴上的左右顺序;
(3)定大小:根据“数轴上两个点表示的数,右边的总比左边的大”确定大小关系。
当堂达标
叁
当堂达标
1.若数轴规定了原点向右的方向为正方向,则原点表示的数为 ,表示负数的点在原点的 ,表示正数的点在原点的 .
0
右侧
左侧
2.在数轴上,表示有理数-3的点与原点的距离为 个单位长度.
3
当堂达标
3.如图所示的图形中,不是数轴的是 ( )
B
4.如图所示,在数轴上A,B 两点所表示的有理数分别为( )
A.3.5和3 B.3.5和-3 C.-3.5和3D.-3.5和-3
C
当堂达标
5.下列说法中,正确的是( )
A.数轴是一条规定了原点、正方向和单位长度的射线
B.离原点近的点所表示的有理数较小
C.数轴上的点可以表示任意有理数
D.原点在数轴的正中间
解析:选项A,数轴是一条规定了原点、正方向和单位长度的射线是错的;选项B,离原点近的点所表示的有理数较小是错的;选项C,数轴上的点可以表示任意有理数是对的;选项D,原点在数轴的正中间是错的.故选C.
C
当堂达标
6.有理数a,b,c 在数轴上的位置如图所示,则( )
A.a,b,c 均是正数
B.a,b,c 均是负数
C.a,b是正数,c 是负数
D.a,b是负数,c 是正数
解析:本题考查数形结合思想,a,b在数轴上原点的左侧,为负数,c在数轴上原点的右侧,为正数.故选D.
D
当堂达标
7.如图所示,在数轴上到原点的距离为3个单位长度的点是( )
A.点D B.点A
C.点A 和点D D.点B 和点C
解析:本题考查数形结合思想,在数轴上到原点的距离为3个单位长度的点有两个,为表示3和-3的点,所以点A和点D符合要求.故选C。
C
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
数形结合思想
分类讨论思想
转化思想
作业布置
详见教材习题
P38-39 T1-5
谢
谢
第二章 有理数及其运算
六年级上册
2 认识有理数
第2课时 数轴
3.写出如图所示的温度计的度数。
课前小测
>
1.下列各有理数中,属于负分数的是( )
A.-2 B.+8.2 C.0 D.-
D
2.比较大小:5 0;2 3。
<
16℃
7℃
0℃
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在一条东西向的马路上,有一个汽车站,汽车站东3 m和7.5 m处分别有一棵柳树和一棵杨树,汽车站西3 m和4.8 m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
情境导入
(1)汽车站东3 m和西3 m分别表示什么意义
(2)汽车站处可以理解为温度计的什么点
请你尝试画图理解.
思考
新知初探
贰
合作探究
探究活动1 数轴的概念与画法
(1)图中温度计上显示的温度各是多少
(2)温度计上的刻度有什么特点
(3)如果把温度计看作是一条标有刻度的直线,那么你能用直线上的点表示有理数吗
合作探究
其实,一个平放的温度计可以看成一条数轴。
画数轴的步骤:
(1)画直线:画一条水平的直线;
(2)取原点:在直线上取一个适当的点作为原点,标上“0”;
(3)定方向:一般规定向右为正方向(画箭头表示);
(4)选长度:选取合适的长度作为单位长度;
(5)标读数:在原点右边标正数,在原点左边标负数。
归纳小结
1.规定了 、 和 的直线称为数轴。
温馨提示:数轴的定义包含三层含义:①数轴是一条直线,可以向两端无限延伸;②数轴有三要素:原点、正方向、单位长度,三者缺一不可;③原点位置的选定,单位长度的大小的确定,正方向的取向,都是根据实际需要“规定”的。同一数轴的单位长度要一致。
原点
单位长度
正方向
2.任何一个有理数都可以用数轴上的一个点来表示。
典例分析
例1 如图,数轴上点A,B,C分别表示什么数?
解: A点表示-2,B点表示2,C点表示0,D点表示-1。
典例分析
例2 画出数轴,并用数轴上的点表示下列各数: , -5, 0, 5, -4, 。
解:如图所示。
-5
0
-4
5
温馨提示:判断数轴画得是否正确,首先检查三要素是否齐全;其次还要注意检查单位长度是否一致,原点左右两边数的顺序是否正确。另外,注意数轴的两端都不能画点,防止把直线画成射线或线段。
合作探究
探究活动2 利用数轴比较有理数的大小
思考·交流
(2)①数轴上的两个点,右边点表示的数与左边点表示的数有怎样的大小关系
②正数、负数在数轴上的什么位置 判断它们的大小。
(1)我们把温度计按如图所示的方式放置,温度变化的规律是什么
归纳小结
有理数的大小比较方法:
(1)数轴上两个点表示的数,右边的总比左边的大。
(2)正数大于0,负数小于0,正数大于负数。
典例分析
例3 画出数轴,用数轴上的点表示下列各数,并用“<”将它们连接起来。
,﹣3.5,0,3,﹣4,﹣ 。
解:把各数表示在数轴上如图,
归纳小结
利用数轴比较有理数的大小的步骤:
(1)画数轴;
(2)表示点:在数轴上描出相应各点,确定各点在数轴上的左右顺序;
(3)定大小:根据“数轴上两个点表示的数,右边的总比左边的大”确定大小关系。
当堂达标
叁
当堂达标
1.若数轴规定了原点向右的方向为正方向,则原点表示的数为 ,表示负数的点在原点的 ,表示正数的点在原点的 .
0
右侧
左侧
2.在数轴上,表示有理数-3的点与原点的距离为 个单位长度.
3
当堂达标
3.如图所示的图形中,不是数轴的是 ( )
B
4.如图所示,在数轴上A,B 两点所表示的有理数分别为( )
A.3.5和3 B.3.5和-3 C.-3.5和3D.-3.5和-3
C
当堂达标
5.下列说法中,正确的是( )
A.数轴是一条规定了原点、正方向和单位长度的射线
B.离原点近的点所表示的有理数较小
C.数轴上的点可以表示任意有理数
D.原点在数轴的正中间
解析:选项A,数轴是一条规定了原点、正方向和单位长度的射线是错的;选项B,离原点近的点所表示的有理数较小是错的;选项C,数轴上的点可以表示任意有理数是对的;选项D,原点在数轴的正中间是错的.故选C.
C
当堂达标
6.有理数a,b,c 在数轴上的位置如图所示,则( )
A.a,b,c 均是正数
B.a,b,c 均是负数
C.a,b是正数,c 是负数
D.a,b是负数,c 是正数
解析:本题考查数形结合思想,a,b在数轴上原点的左侧,为负数,c在数轴上原点的右侧,为正数.故选D.
D
当堂达标
7.如图所示,在数轴上到原点的距离为3个单位长度的点是( )
A.点D B.点A
C.点A 和点D D.点B 和点C
解析:本题考查数形结合思想,在数轴上到原点的距离为3个单位长度的点有两个,为表示3和-3的点,所以点A和点D符合要求.故选C。
C
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
数形结合思想
分类讨论思想
转化思想
作业布置
详见教材习题
P38-39 T1-5
谢
谢
同课章节目录
