2.2第3课时 绝对值与相反数 课件(共28张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册
文档属性
| 名称 | 2.2第3课时 绝对值与相反数 课件(共28张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:12:38 | ||
图片预览







文档简介
(共28张PPT)
第二章 有理数及其运算
六年级上册
2 认识有理数
第3课时 绝对值与相反数
3.写出如图所示的温度计的度数。
课前小测
>
1.下列各有理数中,属于负分数的是( )
A.-2 B.+8.2 C.0 D.-
D
2.比较大小:5 0;2 3。
<
16℃
7℃
0℃
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处。思考:它们行驶的路线相同吗?它们行驶路程的远近相同吗?
新知初探
贰
合作探究
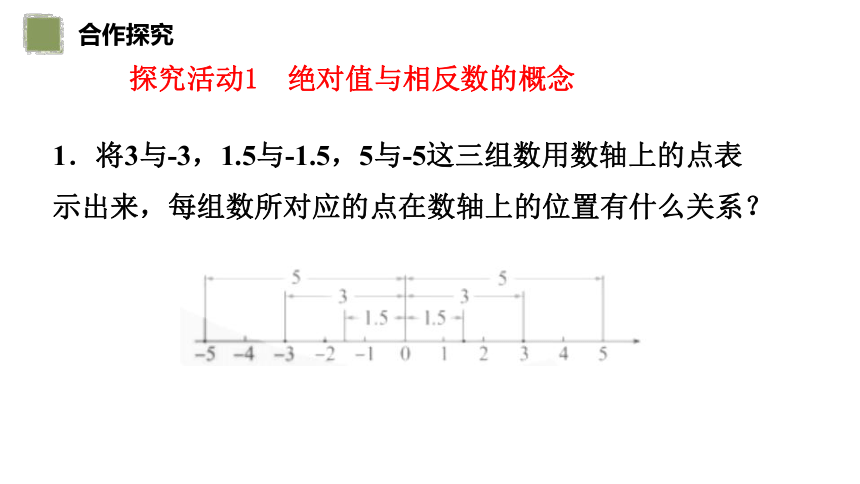
探究活动1 绝对值与相反数的概念
1.将3与-3,1.5与-1.5,5与-5这三组数用数轴上的点表示出来,每组数所对应的点在数轴上的位置有什么关系?
归纳小结
在数轴上,一个数所对应的点与原点之间的距离叫作这个数的绝对值.通常用|a|表示数a的绝对值。
如图,在数轴上,表示5的点与原点的距离是5,就是说,5的绝对值是5,记作|5|=5;表示-3的点与原点的距离是3,就是说,-3的绝对值是3,记作|-3|=3;表示0的点与原点的距离是0,就是说,0的绝对值是0,记作|0|=0。
合作探究
2.(1)3与-3,1.5与-1.5,5与-5这三组数,有何特点?每组数在数轴上所对应的两个点的位置关系有何特点?
答案:每组数中的两个数只有符号不同,它们所对应的两点分别在原点的两侧,到原点的距离相等。
(2)在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
答案:两个;分别表示2与-2
归纳小结
(1)符号不同、绝对值相同的两个数,我们称其中一个数为另一个数的相反数,也称这两个数互为相反数。特别地,0的相反数是0。
(2)在数轴上,表示互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
合作探究
思考·交流
(1)若a是一个任意数,那么-a一定是负数吗?
不是,如a=0时,-a=0;
(2)-(-5)表示什么意义?化简后结果是多少?
-5的相反数,5;
(3)你能借助数轴说明-(-1)=+1吗?
在数轴上,-1在原点左侧,并离原点1个单位长度,则它的相反数在原点左侧,并离原点1个单位长度,这个数是1,即有-(-1)=+1。
典例分析
例1 根据相反数的意义,化简下列各数。
归纳小结
(1)在一个数前面加上“-”号,就变为它的相反数,也就是说,数a的相反数是-a.
(2)若a是一个任意数,则当a>0时,-a<0;当a=0时,-a=0;当a<0时,-a>0.
(3)一般地,有+(+a)= a;-(-a)= a;+(-a)=-a;-(+a)=-a.
(4)多重符号的化简方法:“+”号可以省略不写,化简结果的符号取决于正数前“-”号的个数.若有偶数个“-”号,则把“-”号全部去掉;若有奇数个“-”号,则保留一个“-”号,可简记为“奇负偶正”.
合作探究
探究活动2 绝对值的性质与简单应用
1.绝对值的性质
填一填,从中发现什么规律
|+2|= ,|+8.2|= ;|0|= ;
|-3|= ,|-0.2|= ,|-8.2|= .
归纳小结
(1)正数的绝对值是它本身 ; 负数的绝对值
是它的相反数; 0的绝对值是0 .即
①若a>0,则|a|=a;
②若a<0,则|a|=-a;
③若a=0,则|a|=0.
(2)绝对值的非负性
由绝对值的定义可知:不论有理数a取何值,它的绝对值总是正数或0(通常也称非负数),绝对值具有非负性,即|a|≥0.
典例分析
例2 求下列各数的绝对值:-7,-4.75,10.5.
例3 计算:
(1)|0.32|+|0.3|; (2)|-4.2|-|4.2|.
解:|-7|=7;|-4|=4;|75|=75;|10.5|=10.5。
解:(1)原式=0.32+0.3=0.62;
(2)原式=4.2-4.2=0。
合作探究
思考·交流
2.利用绝对值比较两个负数的大小
(1)在数轴上表示下列各数,并比较它们的大小:
-1.5,-3,-1,-5.
(2)求出(1)中各数的绝对值,并比较它们的大小.
(3)我发现:两个负数比较大小, .
典例分析
例4 比较下列每组数的大小.
(1)-1和-5;
[分析]比较两个负数大小的步骤:
(1)先求它们的绝对值;
(2)比较它们的绝对值的大小;
(3)根据“两个负数比较大小,绝对值大的反而小”比较原数的大小.
解:(1)因为|-1|=1,|-5|=5,(首先求出两个负数的绝对值)1<5,(再比较两个绝对值的大小)
所以-1>-5.(“根据两个负数比较大小,绝对值大的反而小”下结论)
典例分析
(2)因为 ,|-2.7|=2.7,(首先求出两个负数的绝对值)
<2.7,(再比较两个绝对值的大小)
所以 >-2.7.(根据“两个负数比较大小,绝对值大的反而小”下结论)
归纳小结
比较两个负数的大小的步骤:
(1)分别求出两个负数的绝对值;
(2)比较两个绝对值的大小;
(3)根据“两个负数比较大小,绝对值大的反而小”作出正确的判定.
合作探究
3.绝对值的简单应用
某种食品包装袋上标注质量为450 g,对6袋该种食品的实际质量进行检测,检测结果如下( 用正号表示超过标注质量,用负号表示不足标注质量):
-25,+10,-20,+30,+15, -40。
哪袋食品的实际质量更接近标注质量 为什么
解:|-25|=25,|+10|=10,|-20|=20,|+30|=30,|+15|=15,|-40|=40,因为10<15<20<25<30<40,所以第二袋食品的实际质量更接近标准质量.
尝试·思考
当堂达标
叁
当堂达标
2.﹣1.5相反数的是( )
A. B. - C. - D.
A
1. ﹣ 相反数的是( )
A. - B. C. -4 D.4
B
当堂达标
3.绝对值最小的有理数是 .
0
4.若 ,则x的相反数是 .
解析:由绝对值的意义可知 ,再由相反数的意义可知 的相反数为 , 的相反数为 .故填 .
5.
>
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
数形结合思想
分类讨论思想
转化思想
作业布置
详见教材习题
P43 T1-5
谢
谢
第二章 有理数及其运算
六年级上册
2 认识有理数
第3课时 绝对值与相反数
3.写出如图所示的温度计的度数。
课前小测
>
1.下列各有理数中,属于负分数的是( )
A.-2 B.+8.2 C.0 D.-
D
2.比较大小:5 0;2 3。
<
16℃
7℃
0℃
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处。思考:它们行驶的路线相同吗?它们行驶路程的远近相同吗?
新知初探
贰
合作探究
探究活动1 绝对值与相反数的概念
1.将3与-3,1.5与-1.5,5与-5这三组数用数轴上的点表示出来,每组数所对应的点在数轴上的位置有什么关系?
归纳小结
在数轴上,一个数所对应的点与原点之间的距离叫作这个数的绝对值.通常用|a|表示数a的绝对值。
如图,在数轴上,表示5的点与原点的距离是5,就是说,5的绝对值是5,记作|5|=5;表示-3的点与原点的距离是3,就是说,-3的绝对值是3,记作|-3|=3;表示0的点与原点的距离是0,就是说,0的绝对值是0,记作|0|=0。
合作探究
2.(1)3与-3,1.5与-1.5,5与-5这三组数,有何特点?每组数在数轴上所对应的两个点的位置关系有何特点?
答案:每组数中的两个数只有符号不同,它们所对应的两点分别在原点的两侧,到原点的距离相等。
(2)在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
答案:两个;分别表示2与-2
归纳小结
(1)符号不同、绝对值相同的两个数,我们称其中一个数为另一个数的相反数,也称这两个数互为相反数。特别地,0的相反数是0。
(2)在数轴上,表示互为相反数的两个点,位于原点的两侧,且与原点的距离相等。
合作探究
思考·交流
(1)若a是一个任意数,那么-a一定是负数吗?
不是,如a=0时,-a=0;
(2)-(-5)表示什么意义?化简后结果是多少?
-5的相反数,5;
(3)你能借助数轴说明-(-1)=+1吗?
在数轴上,-1在原点左侧,并离原点1个单位长度,则它的相反数在原点左侧,并离原点1个单位长度,这个数是1,即有-(-1)=+1。
典例分析
例1 根据相反数的意义,化简下列各数。
归纳小结
(1)在一个数前面加上“-”号,就变为它的相反数,也就是说,数a的相反数是-a.
(2)若a是一个任意数,则当a>0时,-a<0;当a=0时,-a=0;当a<0时,-a>0.
(3)一般地,有+(+a)= a;-(-a)= a;+(-a)=-a;-(+a)=-a.
(4)多重符号的化简方法:“+”号可以省略不写,化简结果的符号取决于正数前“-”号的个数.若有偶数个“-”号,则把“-”号全部去掉;若有奇数个“-”号,则保留一个“-”号,可简记为“奇负偶正”.
合作探究
探究活动2 绝对值的性质与简单应用
1.绝对值的性质
填一填,从中发现什么规律
|+2|= ,|+8.2|= ;|0|= ;
|-3|= ,|-0.2|= ,|-8.2|= .
归纳小结
(1)正数的绝对值是它本身 ; 负数的绝对值
是它的相反数; 0的绝对值是0 .即
①若a>0,则|a|=a;
②若a<0,则|a|=-a;
③若a=0,则|a|=0.
(2)绝对值的非负性
由绝对值的定义可知:不论有理数a取何值,它的绝对值总是正数或0(通常也称非负数),绝对值具有非负性,即|a|≥0.
典例分析
例2 求下列各数的绝对值:-7,-4.75,10.5.
例3 计算:
(1)|0.32|+|0.3|; (2)|-4.2|-|4.2|.
解:|-7|=7;|-4|=4;|75|=75;|10.5|=10.5。
解:(1)原式=0.32+0.3=0.62;
(2)原式=4.2-4.2=0。
合作探究
思考·交流
2.利用绝对值比较两个负数的大小
(1)在数轴上表示下列各数,并比较它们的大小:
-1.5,-3,-1,-5.
(2)求出(1)中各数的绝对值,并比较它们的大小.
(3)我发现:两个负数比较大小, .
典例分析
例4 比较下列每组数的大小.
(1)-1和-5;
[分析]比较两个负数大小的步骤:
(1)先求它们的绝对值;
(2)比较它们的绝对值的大小;
(3)根据“两个负数比较大小,绝对值大的反而小”比较原数的大小.
解:(1)因为|-1|=1,|-5|=5,(首先求出两个负数的绝对值)1<5,(再比较两个绝对值的大小)
所以-1>-5.(“根据两个负数比较大小,绝对值大的反而小”下结论)
典例分析
(2)因为 ,|-2.7|=2.7,(首先求出两个负数的绝对值)
<2.7,(再比较两个绝对值的大小)
所以 >-2.7.(根据“两个负数比较大小,绝对值大的反而小”下结论)
归纳小结
比较两个负数的大小的步骤:
(1)分别求出两个负数的绝对值;
(2)比较两个绝对值的大小;
(3)根据“两个负数比较大小,绝对值大的反而小”作出正确的判定.
合作探究
3.绝对值的简单应用
某种食品包装袋上标注质量为450 g,对6袋该种食品的实际质量进行检测,检测结果如下( 用正号表示超过标注质量,用负号表示不足标注质量):
-25,+10,-20,+30,+15, -40。
哪袋食品的实际质量更接近标注质量 为什么
解:|-25|=25,|+10|=10,|-20|=20,|+30|=30,|+15|=15,|-40|=40,因为10<15<20<25<30<40,所以第二袋食品的实际质量更接近标准质量.
尝试·思考
当堂达标
叁
当堂达标
2.﹣1.5相反数的是( )
A. B. - C. - D.
A
1. ﹣ 相反数的是( )
A. - B. C. -4 D.4
B
当堂达标
3.绝对值最小的有理数是 .
0
4.若 ,则x的相反数是 .
解析:由绝对值的意义可知 ,再由相反数的意义可知 的相反数为 , 的相反数为 .故填 .
5.
>
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
数形结合思想
分类讨论思想
转化思想
作业布置
详见教材习题
P43 T1-5
谢
谢
同课章节目录
