2.4 第3课时 有理数的除法 课件(共31张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册
文档属性
| 名称 | 2.4 第3课时 有理数的除法 课件(共31张PPT) 2025-2026学年数学鲁教版(五四制)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:22:09 | ||
图片预览











文档简介
(共31张PPT)
第二章 有理数及其运算
六年级上册
4 有理数的乘除运算
第3课时 有理数的除法
课前小测
3.计算: 。
2.计算:18÷9= ;1÷ = 。
A
2
3
1. 计算(-1)×(-3)的结果为( )
A.3 B. C.-3 D.-4
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
小林说:小佳由3×2=6知道6÷3=2,那么(-3)×(﹣2)=6,类似地有6÷(﹣3)=﹣2,6÷(﹣2)=﹣3,对吗?
小佳:由以前学过的乘法与除法的关系,感觉这应是正确的,但怎样计算这样的除法更简便呢?
被除数、除数、商之间的关系.
思考
被除数=除数×商
新知初探
贰
合作探究
探究活动1 有理数的除法运算律法则一
活动一 根据“除法是乘法的逆运算”填空:
(–2)×3=–6;(–6)÷3= ;
2×(–3)=–6;(–6)÷(–3)= ;
(–2)×(–3)=6;6÷(–3)= ;
0×(-3)=0;0÷(-3)= .
交流:观察上面的算式及计算结果,你有什么发现?换一些算式再试一试.
2
-2
-2
0
合作探究
猜想
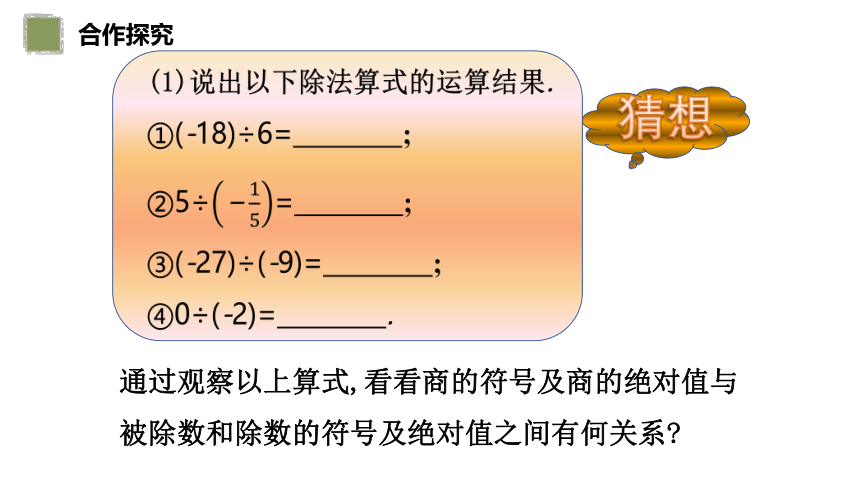
(1)说出以下除法算式的运算结果.
①(-18)÷6= ;
②5÷= ;
③(-27)÷(-9)= ;
④0÷(-2)= .
通过观察以上算式,看看商的符号及商的绝对值与被除数和除数的符号及绝对值之间有何关系
归纳小结
有理数的除法法则:
两数相除,同号得正,异号得负,并把 绝对值相除。
0除以任何非0的数都得0。
注意:0不能作除数。
(1)(-15)÷(-3); (2)(-15)÷(- );
(3)(-0.75)÷0.25; (4)(-12)÷(- )÷(-100).
典例分析
例1 计算:
解:(1)(-15)÷(-3)=+(15÷3)=5;
(2)(-15)÷(- )=+(15÷ )=48;
(3)(-0.75)÷0.25=-(0.75÷0.25)=-3;
(4)(-12)÷(- )÷(-100)=+(12÷ )÷(-100)
=144÷(-100)=-(144÷100)=-1.44.
归纳小结
首先确定商的符号,然后再把绝对值相除.第(4)小题要按顺序从左到右进行计算.
另外注意:负数在有理数运算中一定要加上括号.
合作探究
尝试·思考
比较下列各组数的计算结果,你能得到什么结论?换一些算式再试一试。
探究活动2 有理数的除法运算律法则二
(1)1÷与1×.
(2)0.8÷与0.8×.
(3)÷与×(-4).
归纳小结
有理数的除法法则:
除以一个数等于乘这个数的倒数。
这个法则也可表示成a÷b=a× (b≠0)。
温馨提示:利用该法则可以将有理数的除法转化为乘法,所以可以利用乘法的运算律简化运算.
典例分析
例2 计算:
(1)(-18)÷(- ); (2)16÷(- )÷(- ).
解:(1)(-18)÷(- )=(-18)×(- )=18× =27;
(2)16÷(- )÷(- )=16×(- )×(- )
=16×(- )×(- )= .
思考:(1)上述计算过程,还可以怎样写?
典例分析
解:(1)(-18)÷(- )=18÷ =18× =27;
(2)16÷(- )÷(- )=16÷ ÷ =16× ×
=16× × = .
追问:(1)将除法转化为乘法有什么好处?
(2)有理数的乘除法与小学数学中的乘除法相比较,有哪些相同点和不同点?
归纳小结
对于除法的两个法则,在计算时根据具体情况,灵活选用,一般在能整除的情况下,应用法则一比较方便,在不能整除的情况下应选用法则二进行计算,且运用法则二可适当选取运算律简化运算.注意,除法的混合运算,要按从左往右的顺序进行,切记看清运算,不要混淆了乘除运算.
典例分析
例3(补充) 计算:72×(-8)÷(-12).
〔解析〕乘除法是同级运算,进行乘除混合运算时,可从左至右逐步运算,还可以将式子中的除法变为乘法,直接进行乘法运算.
典例分析
72×(-8)÷(-12)=-(72×8)÷(-12)
=-576÷(-12)
=48.
72×(-8)÷(-12)
=+
=48.
解法1
解法2
典例分析
例4 (补充)计算:(-5)÷(-7)÷(-15).
解: (-5)÷(-7)÷(-15)=-=- .
〔解析〕 三个数连除,先确定商的符号,再将除法转化为乘法,最后利用乘法法则进行计算.
归纳小结
解题技巧:
(1)有理数乘除法法则遵循“符号优先”原则,即先确定符号,再把绝对值相乘除.
(2)对于多个有理数相乘除,运算时可以从左到右进行,也可把除法转化成乘法后再进行计算.
(3)要正确使用符号法则,确定各步运算结果的符号.
当堂达标
叁
当堂达标
1.当a 时,=1,当a 时,= -1.
解析: 由=1得|a|=a,因为a不能为零,所以a为正数,即a>0;当=-1时,a为负数,即a<0.
>0
<0
当堂达标
2.当m= 时,2÷(3m+1)没有意义;
当n= 时,(1-2n) ÷11=0.
解析: 当除数等于0时无意义,所以3m+1=0,所以m=- .当(1-2n) ÷11=0时,分子应等于0,即1-2n=0,所以n=.
-
当堂达标
3.两数的积是-1,其中一个数是-1,那么
另一个数是 .
解析: 另一个数应等于-1除以-1.
(-1)÷=(-1)÷=1×=.故填.
当堂达标
4.计算:÷.
解:÷=×(-7)=- .
当堂达标
5.计算:(-3)×÷.
解: (-3)×÷
=(-3)××(-4)
=-30.
当堂达标
6.计算:(-3)÷.
解: (-3)÷
=(-3)÷
=- .
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
转化思想
作业布置
详见教材习题
P71-72 T1-5
谢
谢
第二章 有理数及其运算
六年级上册
4 有理数的乘除运算
第3课时 有理数的除法
课前小测
3.计算: 。
2.计算:18÷9= ;1÷ = 。
A
2
3
1. 计算(-1)×(-3)的结果为( )
A.3 B. C.-3 D.-4
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
小林说:小佳由3×2=6知道6÷3=2,那么(-3)×(﹣2)=6,类似地有6÷(﹣3)=﹣2,6÷(﹣2)=﹣3,对吗?
小佳:由以前学过的乘法与除法的关系,感觉这应是正确的,但怎样计算这样的除法更简便呢?
被除数、除数、商之间的关系.
思考
被除数=除数×商
新知初探
贰
合作探究
探究活动1 有理数的除法运算律法则一
活动一 根据“除法是乘法的逆运算”填空:
(–2)×3=–6;(–6)÷3= ;
2×(–3)=–6;(–6)÷(–3)= ;
(–2)×(–3)=6;6÷(–3)= ;
0×(-3)=0;0÷(-3)= .
交流:观察上面的算式及计算结果,你有什么发现?换一些算式再试一试.
2
-2
-2
0
合作探究
猜想
(1)说出以下除法算式的运算结果.
①(-18)÷6= ;
②5÷= ;
③(-27)÷(-9)= ;
④0÷(-2)= .
通过观察以上算式,看看商的符号及商的绝对值与被除数和除数的符号及绝对值之间有何关系
归纳小结
有理数的除法法则:
两数相除,同号得正,异号得负,并把 绝对值相除。
0除以任何非0的数都得0。
注意:0不能作除数。
(1)(-15)÷(-3); (2)(-15)÷(- );
(3)(-0.75)÷0.25; (4)(-12)÷(- )÷(-100).
典例分析
例1 计算:
解:(1)(-15)÷(-3)=+(15÷3)=5;
(2)(-15)÷(- )=+(15÷ )=48;
(3)(-0.75)÷0.25=-(0.75÷0.25)=-3;
(4)(-12)÷(- )÷(-100)=+(12÷ )÷(-100)
=144÷(-100)=-(144÷100)=-1.44.
归纳小结
首先确定商的符号,然后再把绝对值相除.第(4)小题要按顺序从左到右进行计算.
另外注意:负数在有理数运算中一定要加上括号.
合作探究
尝试·思考
比较下列各组数的计算结果,你能得到什么结论?换一些算式再试一试。
探究活动2 有理数的除法运算律法则二
(1)1÷与1×.
(2)0.8÷与0.8×.
(3)÷与×(-4).
归纳小结
有理数的除法法则:
除以一个数等于乘这个数的倒数。
这个法则也可表示成a÷b=a× (b≠0)。
温馨提示:利用该法则可以将有理数的除法转化为乘法,所以可以利用乘法的运算律简化运算.
典例分析
例2 计算:
(1)(-18)÷(- ); (2)16÷(- )÷(- ).
解:(1)(-18)÷(- )=(-18)×(- )=18× =27;
(2)16÷(- )÷(- )=16×(- )×(- )
=16×(- )×(- )= .
思考:(1)上述计算过程,还可以怎样写?
典例分析
解:(1)(-18)÷(- )=18÷ =18× =27;
(2)16÷(- )÷(- )=16÷ ÷ =16× ×
=16× × = .
追问:(1)将除法转化为乘法有什么好处?
(2)有理数的乘除法与小学数学中的乘除法相比较,有哪些相同点和不同点?
归纳小结
对于除法的两个法则,在计算时根据具体情况,灵活选用,一般在能整除的情况下,应用法则一比较方便,在不能整除的情况下应选用法则二进行计算,且运用法则二可适当选取运算律简化运算.注意,除法的混合运算,要按从左往右的顺序进行,切记看清运算,不要混淆了乘除运算.
典例分析
例3(补充) 计算:72×(-8)÷(-12).
〔解析〕乘除法是同级运算,进行乘除混合运算时,可从左至右逐步运算,还可以将式子中的除法变为乘法,直接进行乘法运算.
典例分析
72×(-8)÷(-12)=-(72×8)÷(-12)
=-576÷(-12)
=48.
72×(-8)÷(-12)
=+
=48.
解法1
解法2
典例分析
例4 (补充)计算:(-5)÷(-7)÷(-15).
解: (-5)÷(-7)÷(-15)=-=- .
〔解析〕 三个数连除,先确定商的符号,再将除法转化为乘法,最后利用乘法法则进行计算.
归纳小结
解题技巧:
(1)有理数乘除法法则遵循“符号优先”原则,即先确定符号,再把绝对值相乘除.
(2)对于多个有理数相乘除,运算时可以从左到右进行,也可把除法转化成乘法后再进行计算.
(3)要正确使用符号法则,确定各步运算结果的符号.
当堂达标
叁
当堂达标
1.当a 时,=1,当a 时,= -1.
解析: 由=1得|a|=a,因为a不能为零,所以a为正数,即a>0;当=-1时,a为负数,即a<0.
>0
<0
当堂达标
2.当m= 时,2÷(3m+1)没有意义;
当n= 时,(1-2n) ÷11=0.
解析: 当除数等于0时无意义,所以3m+1=0,所以m=- .当(1-2n) ÷11=0时,分子应等于0,即1-2n=0,所以n=.
-
当堂达标
3.两数的积是-1,其中一个数是-1,那么
另一个数是 .
解析: 另一个数应等于-1除以-1.
(-1)÷=(-1)÷=1×=.故填.
当堂达标
4.计算:÷.
解:÷=×(-7)=- .
当堂达标
5.计算:(-3)×÷.
解: (-3)×÷
=(-3)××(-4)
=-30.
当堂达标
6.计算:(-3)÷.
解: (-3)÷
=(-3)÷
=- .
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
转化思想
作业布置
详见教材习题
P71-72 T1-5
谢
谢
同课章节目录
