2.5 有理数的乘方 第1课时 有理数的乘方 课件(共25张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册
文档属性
| 名称 | 2.5 有理数的乘方 第1课时 有理数的乘方 课件(共25张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 14:54:07 | ||
图片预览








文档简介
(共25张PPT)
第二章 有理数及其运算
六年级上册
5 有理数的乘方
第1课时 有理数的乘方
课前小测
D
22=4
23=8
1.正方形的边长为2,其面积是多少
2.棱长为2的正方体的体积为多少
3.若a2=16,|b|=5有意义,则a+b所有的可能值是( )
A.-1 B.-1或-9 C.1或9 D.±1或±9
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.大臣说:“就在这个棋盘上放些米粒吧.第一格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒,…,直到第64格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣却说:“就怕您的国库里没有这么多米!”
聪明的同学们,你估计国王有这么多米吗?
(友情提示:100粒米粒约重2.5克)
新知初探
贰
合作探究
探究活动1 乘方的意义
讨论分析情境导入中的问题:
解析:根据大臣的要求,第一个放1粒米,第二格放21=2粒米,第三格放2×2=22=4粒米,第四格放2×2×2=23=8粒米,…,仅第64格(即最后一格)放米2×2×2×…×2=263粒,其重量为263÷100×2.5÷1000000≈2250亿吨,显然,国王的国库里没有这么多粒米!
一般地,n个相同因数a相乘,记作an,即
这种求n个相同因数a的积的运算叫作乘方,乘方的结果叫作幂,a叫作底数,n叫作指数,an读作“a的n次幂”(或“a的n次方”).
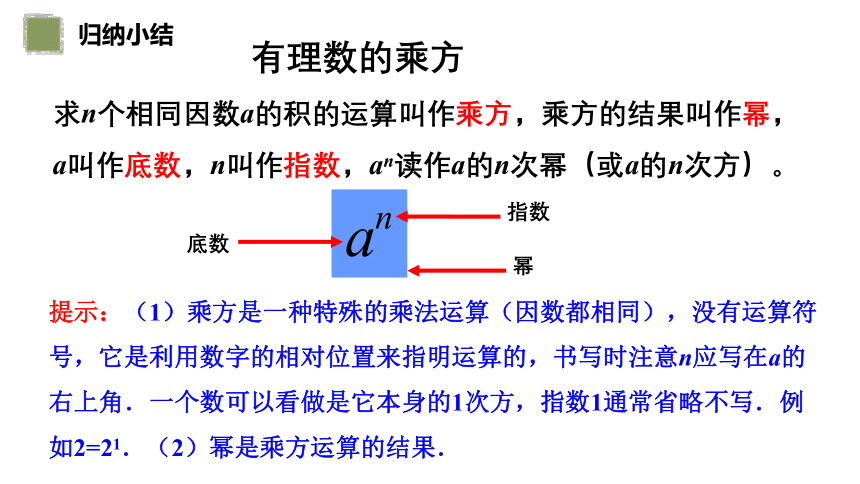
归纳小结
有理数的乘方
求n个相同因数a的积的运算叫作乘方,乘方的结果叫作幂,a叫作底数,n叫作指数,an读作a的n次幂(或a的n次方)。
底数
指数
幂
提示:(1)乘方是一种特殊的乘法运算(因数都相同),没有运算符号,它是利用数字的相对位置来指明运算的,书写时注意n应写在a的右上角.一个数可以看做是它本身的1次方,指数1通常省略不写.例如2=21.(2)幂是乘方运算的结果.
例1 的4次幂应记为( )
A. B. C. D.
例题分析
思考:该幂的底数是什么?指数是什么?如何写成幂的形式?
解析:A选项中底数为2,B选项中底数为 ,D选项中表示 的4次幂的相反数,也不符合题意,根据幂的意义,可知应选C.
C
练习:
(1)(-5)×(-5)×(-5)×(-5)×(-5)写成乘方的式子是 .
(2)在210中,2是 数,10是 数,读作 ,表示 个 相乘.
归纳小结
(1)乘方具有双重意义,一是它是一种运算——求相同因数的积的运算;二是它表示乘方运算的结果——幂.
(2)在书写幂时注意底数,当底数是负数、分数或式子时,应加上括号,再写指数.
(3)负数的乘方与乘方的相反数不同.例如:
(-2)4=(-2)×(-2)×(-2)×(-2)=16,
而-24=-2×2×2×2=-16.
(4)平方等于它本身的数是0和1,立方等于它本身的数是0、1和-1.
合作探究
活动 请填写下表:
探究活动2 有理数的乘方运算
议一议:根据上表,你能总结出哪些规律?
归纳小结
负数的奇次幂是 数,负数的偶次幂是 数.
正数的任何次幂都是 数,0的任何正整数次幂都是 .
温馨提示:在计算中,可以把乘方运算转化成乘法运算.
负
正
0
正
(1)(-5)4;(2)-54;(3)(- )3;(4)- .
典例分析
例2 计算:
思考:(1)算式(1)与(2)、(3)与(4)计算结果相同吗?为什么?
(2)各算式中幂的符号如何确定?绝对值如何确定?
解:(1)(-5)4=54=5×5×5×5=625;
(2)-54=-5×5×5×5=-625;
(3)(- )3=- × × =- ;
(4)- =- = .
归纳小结
有理数乘方运算的一般步骤
(1)定符号:幂的符号是由底数和指数决定的,通常是“先看底数,再看指数”.
(2)定绝对值:即计算底数绝对值的幂.
(2)运算中出现符号错误,如(-5)4=-625.如按乘方的定义,将乘方运算先转为乘法运算再进行计算,并注意乘方运算符号法则的运用.
提醒
(1)混淆乘方与乘法的概念,如把54当作5×4来计算;
(3)10的n次幂的特点是1后面有n个0.两个数互为相反数,偶次方相等,奇次方互为相反数.
合作探究
探究活动3 有理数的乘方运算应用
计算:(1)102,103,104,105; (2)(-10)2,(-10)3,(-10)4,(-10)5.
观察·交流
观察计算结果,你能发现什么规律?与同伴进行交流.
观察·思考
有一张厚度是0.1 mm的纸,将它对折1次后,厚度为2×0.1 mm.
(1)将这张纸对折2次后,厚度为多少毫米
(2)假设可以将这张纸对折20次,那么对折20次后厚度为多少米
(3)如果每层楼的平均高度为3 m,那么这张纸对折20次后大约有多少层楼高
解:(1)22×0.1=0.4(mm);
(2)220×0.1=104857.6(mm);
(3)104857.6÷1000÷3≈35.即约等于35层楼高.
典例分析
尝试·思考
你见过拉面师傅拉面条吗 拉面师傅将一根粗面条拉长、两头捏合,再拉长、捏合,重复这样,就拉成许多根细面条了.据报道,在一次比赛中,某拉面师傅用1 kg面粉拉出约209万根面条,你认为该报道是怎样得出“209万根”这个结果的
解析:210=1024≈103,则220≈106,即约为100万,所以221约为200万,约拉21次.
第一次
第二次
第三次
…
当指数不断增加时,底数为2的幂的增长速度相当快.
当堂达标
叁
当堂达标
1.下面各式计算结果正确的是 ( )
A.-22=-4 B.-(-2)2=4
C.(-3)2=6 D.(-3)3=27
A
解析: 在计算乘方时,要注意底数和符号,B选项,-(-2)2=-4,C选项,(-3)2=9,D选项,(-3)3=-27.故选A.
当堂达标
2.填空.
(1)(-4)×(-4)×(-4)×(-4)×(-4)写成乘方的式子是 ;
(2)中,底数是 ,指数是 ;
(3)一个数的5次幂是负数,则这个数的7次幂是 数,4次幂是 数.
(- 4)5
当堂达标
3.计算.
(1)(-1)258; (2)-12024; (3)(-0.2)2;
(4)-(-14)2; (5)-.
解:(1)(-1)258=1. (2)-12024=-1.
(3)(-0.2)2=0.04. (4)-(-14)2=-196.
(5)-=.
当堂达标
4.如图是某种细胞分裂示意图,这种细胞每过30min便由1个分裂成2个.根据此规律回答:
(1)这样的一个细胞经过第四个30min后可分裂成多少个细胞?
(2)这样的一个细胞经过3h后可分裂成多少个细胞?
解:(1)第四个30min后可以分裂成24=16(个)细胞;
(2)因为30h=180min,180÷30=6,即这样的一个细胞经过3h后可分裂成26=64(个)细胞.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
数学思想:
转化思想
作业布置
详见教材习题
P76 T1-3
谢
谢
第二章 有理数及其运算
六年级上册
5 有理数的乘方
第1课时 有理数的乘方
课前小测
D
22=4
23=8
1.正方形的边长为2,其面积是多少
2.棱长为2的正方体的体积为多少
3.若a2=16,|b|=5有意义,则a+b所有的可能值是( )
A.-1 B.-1或-9 C.1或9 D.±1或±9
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.大臣说:“就在这个棋盘上放些米粒吧.第一格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒,…,直到第64格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣却说:“就怕您的国库里没有这么多米!”
聪明的同学们,你估计国王有这么多米吗?
(友情提示:100粒米粒约重2.5克)
新知初探
贰
合作探究
探究活动1 乘方的意义
讨论分析情境导入中的问题:
解析:根据大臣的要求,第一个放1粒米,第二格放21=2粒米,第三格放2×2=22=4粒米,第四格放2×2×2=23=8粒米,…,仅第64格(即最后一格)放米2×2×2×…×2=263粒,其重量为263÷100×2.5÷1000000≈2250亿吨,显然,国王的国库里没有这么多粒米!
一般地,n个相同因数a相乘,记作an,即
这种求n个相同因数a的积的运算叫作乘方,乘方的结果叫作幂,a叫作底数,n叫作指数,an读作“a的n次幂”(或“a的n次方”).
归纳小结
有理数的乘方
求n个相同因数a的积的运算叫作乘方,乘方的结果叫作幂,a叫作底数,n叫作指数,an读作a的n次幂(或a的n次方)。
底数
指数
幂
提示:(1)乘方是一种特殊的乘法运算(因数都相同),没有运算符号,它是利用数字的相对位置来指明运算的,书写时注意n应写在a的右上角.一个数可以看做是它本身的1次方,指数1通常省略不写.例如2=21.(2)幂是乘方运算的结果.
例1 的4次幂应记为( )
A. B. C. D.
例题分析
思考:该幂的底数是什么?指数是什么?如何写成幂的形式?
解析:A选项中底数为2,B选项中底数为 ,D选项中表示 的4次幂的相反数,也不符合题意,根据幂的意义,可知应选C.
C
练习:
(1)(-5)×(-5)×(-5)×(-5)×(-5)写成乘方的式子是 .
(2)在210中,2是 数,10是 数,读作 ,表示 个 相乘.
归纳小结
(1)乘方具有双重意义,一是它是一种运算——求相同因数的积的运算;二是它表示乘方运算的结果——幂.
(2)在书写幂时注意底数,当底数是负数、分数或式子时,应加上括号,再写指数.
(3)负数的乘方与乘方的相反数不同.例如:
(-2)4=(-2)×(-2)×(-2)×(-2)=16,
而-24=-2×2×2×2=-16.
(4)平方等于它本身的数是0和1,立方等于它本身的数是0、1和-1.
合作探究
活动 请填写下表:
探究活动2 有理数的乘方运算
议一议:根据上表,你能总结出哪些规律?
归纳小结
负数的奇次幂是 数,负数的偶次幂是 数.
正数的任何次幂都是 数,0的任何正整数次幂都是 .
温馨提示:在计算中,可以把乘方运算转化成乘法运算.
负
正
0
正
(1)(-5)4;(2)-54;(3)(- )3;(4)- .
典例分析
例2 计算:
思考:(1)算式(1)与(2)、(3)与(4)计算结果相同吗?为什么?
(2)各算式中幂的符号如何确定?绝对值如何确定?
解:(1)(-5)4=54=5×5×5×5=625;
(2)-54=-5×5×5×5=-625;
(3)(- )3=- × × =- ;
(4)- =- = .
归纳小结
有理数乘方运算的一般步骤
(1)定符号:幂的符号是由底数和指数决定的,通常是“先看底数,再看指数”.
(2)定绝对值:即计算底数绝对值的幂.
(2)运算中出现符号错误,如(-5)4=-625.如按乘方的定义,将乘方运算先转为乘法运算再进行计算,并注意乘方运算符号法则的运用.
提醒
(1)混淆乘方与乘法的概念,如把54当作5×4来计算;
(3)10的n次幂的特点是1后面有n个0.两个数互为相反数,偶次方相等,奇次方互为相反数.
合作探究
探究活动3 有理数的乘方运算应用
计算:(1)102,103,104,105; (2)(-10)2,(-10)3,(-10)4,(-10)5.
观察·交流
观察计算结果,你能发现什么规律?与同伴进行交流.
观察·思考
有一张厚度是0.1 mm的纸,将它对折1次后,厚度为2×0.1 mm.
(1)将这张纸对折2次后,厚度为多少毫米
(2)假设可以将这张纸对折20次,那么对折20次后厚度为多少米
(3)如果每层楼的平均高度为3 m,那么这张纸对折20次后大约有多少层楼高
解:(1)22×0.1=0.4(mm);
(2)220×0.1=104857.6(mm);
(3)104857.6÷1000÷3≈35.即约等于35层楼高.
典例分析
尝试·思考
你见过拉面师傅拉面条吗 拉面师傅将一根粗面条拉长、两头捏合,再拉长、捏合,重复这样,就拉成许多根细面条了.据报道,在一次比赛中,某拉面师傅用1 kg面粉拉出约209万根面条,你认为该报道是怎样得出“209万根”这个结果的
解析:210=1024≈103,则220≈106,即约为100万,所以221约为200万,约拉21次.
第一次
第二次
第三次
…
当指数不断增加时,底数为2的幂的增长速度相当快.
当堂达标
叁
当堂达标
1.下面各式计算结果正确的是 ( )
A.-22=-4 B.-(-2)2=4
C.(-3)2=6 D.(-3)3=27
A
解析: 在计算乘方时,要注意底数和符号,B选项,-(-2)2=-4,C选项,(-3)2=9,D选项,(-3)3=-27.故选A.
当堂达标
2.填空.
(1)(-4)×(-4)×(-4)×(-4)×(-4)写成乘方的式子是 ;
(2)中,底数是 ,指数是 ;
(3)一个数的5次幂是负数,则这个数的7次幂是 数,4次幂是 数.
(- 4)5
当堂达标
3.计算.
(1)(-1)258; (2)-12024; (3)(-0.2)2;
(4)-(-14)2; (5)-.
解:(1)(-1)258=1. (2)-12024=-1.
(3)(-0.2)2=0.04. (4)-(-14)2=-196.
(5)-=.
当堂达标
4.如图是某种细胞分裂示意图,这种细胞每过30min便由1个分裂成2个.根据此规律回答:
(1)这样的一个细胞经过第四个30min后可分裂成多少个细胞?
(2)这样的一个细胞经过3h后可分裂成多少个细胞?
解:(1)第四个30min后可以分裂成24=16(个)细胞;
(2)因为30h=180min,180÷30=6,即这样的一个细胞经过3h后可分裂成26=64(个)细胞.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
数学思想:
转化思想
作业布置
详见教材习题
P76 T1-3
谢
谢
同课章节目录
