3.1 认识代数式 第2课时 代数式 课件(共23张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册
文档属性
| 名称 | 3.1 认识代数式 第2课时 代数式 课件(共23张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 15:02:37 | ||
图片预览








文档简介
(共23张PPT)
第三章 整式及其加减
六年级上册
1 认识代数式
第2课时 代数式
课前小测
4a
a2
(2m+0.5n)
(1)边长为a cm的正方形的周长是 cm,面积是 cm2;
(2)钢笔每支2元,铅笔每支0.5元,m支钢笔和n支铅笔共 元;
(3)温度由2 ℃下降t ℃后是 ℃。
(2-t)
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
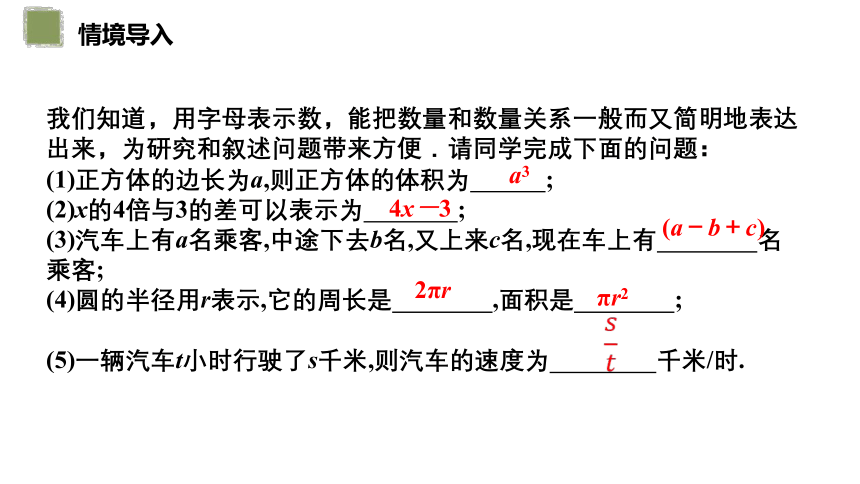
我们知道,用字母表示数,能把数量和数量关系一般而又简明地表达出来,为研究和叙述问题带来方便.请同学完成下面的问题:
(1)正方体的边长为a,则正方体的体积为 ;
(2)x的4倍与3的差可以表示为 ;
(3)汽车上有a名乘客,中途下去b名,又上来c名,现在车上有 名乘客;
(4)圆的半径用r表示,它的周长是 ,面积是 ;
(5)一辆汽车t小时行驶了s千米,则汽车的速度为 千米/时.
a3
4x-3
(a-b+c)
2πr
πr2
新知初探
贰
合作探究
探究活动1 代数式的意义
观察 思考
上面各问题中得到的含有字母的式子,你发现它们包含哪些运算?与同伴交流.
a3
4x-3
(a-b+c)
2πr
πr2
归纳小结
像上面这些式子,除了含有数字或表示数的字母之外,通常还含有运算符号(加、减、乘、除、乘方、开方),这样的式子都是代数式.
单独一个数或一个字母也是代数式.
温馨提示:(1)代数式中不含“=”“>”“<”“≠”等符号.
(2)代数式可以简明地描述许多实际问题中的数量关系.
典例分析
阅读·思考:教材第100页“代数”的由来.
例1 设字母a表示甲数,字母b表示乙数,用代数式表示:
(1)甲、乙两数的差的2倍;
(2)甲数的 与乙数的 的差;
(3)甲、乙两数的差的立方;
(4)甲、乙两数的平方和.
解:(1)2(a-b); (2) a- b;
(3)(a-b)3; (4)a2+b2.
归纳小结
1.在把文字叙述的语句“翻译”成代数式时,首先要正确理解这一语句的数学含义;同时,要正确判断语句中所给出的各种运算的顺序.
2.代数式的书写格式要求:
(1)字母与字母相乘,乘号通常写作“ ”或省略不写,如v×t写成v t或vt,而数字与数字相乘仍用“×”号;
(2)数字与字母相乘,数字应写在字母前面,如a×3=3a;
(3)带分数与字母相乘时,应先把带分数化成假分数后再与字母相乘,如 2 ×a= a;
(4)除法运算一般写成分数形式,如s÷v应写为 ;
(5)在一些实际问题中,所列式子是积或商的形式,把单位名称直接写在后面,若是和或差的形式则必须把式子用括号括起来,再将单位名称写在式子的后面,如ab厘米、(a+b)千克等.
合作探究
针对训练:教材第99页随堂练习第1,2题.
例2 与文字语言叙述下列代数式:
(1)x+y;(2) (x-y);(3)(x+y)2;(4)x3+y3.
解:(1)x与y两数的和;(2)x与y两数差的 ;
(3)x与y两数和的平方;(4)x与y两数的立方和.
归纳小结:用语言表达代数式的意义,一定要正确判断代数式中含有的各种运算及其顺序,要以不引起误解为前提,灵活运用和、差、积、商、倍、倒数等词语.
合作探究
探究活动2 代数式的实际背景或几何意义
例3 甲、乙两地相距150km,一辆汽车的行驶速度为a km/h,用代数式表示:
(1)这辆汽车从甲地到乙地需要行驶多长时间?
(2)若速度增加2km/h,则需要多长时间?加速后可以早到多长时间?
解:(1)这辆汽车从甲地到乙地需要行驶 h.
(2)如果速度增加2km/h,那么行驶速度就是(a+2)km/h,所以从
甲地到乙地需要行驶 h.加速后可以早到( - )h.
合作探究
思考·交流:
代数式10x+5y可以表示哪些生活中的问题?与同伴交流.
如果用x(单位:m/s)表示小明跑步的速度,用y(单位:m/s)表示小明走路的速度,那么10x+5y表示他跑步10 s和走路5 s所经过的路程;如果用x和y分别表示1元和5角硬币的枚数,那么10x+5y就表示x枚1元硬币和y枚5角硬币共是多少角钱.
针对练习:教材第102页随堂练习第1,4题;教材第103页
习题第3题.
归纳小结
解决这类问题的关键是熟知常见问题如行程、工程、销售等问题中的数量关系,以及一些面积、体积公式,在书写代数式时,若是和或差的形式必须把式子用括号括起来,将单位名称写在式子的后面.
当堂达标
叁
当堂达标
1.下列各式:
(1)a+b=5; (2)5a-3y ; (3)2;
(4)n ; (5)2(a+b)+7; (6) ;
(7)2+7-6; (8)23; (9)x+5>3.
其中哪些是代数式,哪些不是代数式
解析:代数式是用运算符号(加、减、乘、除、乘方等)把数和字母连接而成的式子,而用“=”“≠”“<”“>”“≤”“≥”等关系符号连接而成的式子都不是代数式.
解:(2)(3)(4)(5)(6)(7)(8)是代数式,而(1)(9)不是代数式.
当堂达标
解析: 根据代数式的书写要求,不能出现带分数,故①不符合;数字与字母相乘时,乘号省略或用“ ”表示,并且数字在前,故②不符合;含有字母的除法中,一般应写成分数的形式,故③不符合.故选D.
D
2.下列各式中符合代数式书写要求的个数为 ( )
① x2y; ②y×3; ③ab÷2; ④ .
A.4 B.3 C.2 D.1
当堂达标
3.对于代数式2x-3y,下列读法不正确的有 ( )
A.2x 减去3y
B.2x与3y 的差
C.x的2倍与y 的3倍的差
D.2乘x 减去3乘y
解析: 代数式的读法有两种,一种是按运算关系读,另一种是按运算结果来读.无论哪一种,都要注意运算顺序.A,B,C的读法都可以与代数式相对应,D有可能误理解为(2x-3)y.故选D.
D
当堂达标
4.下列选项中的量不能用“8m”表示的是( )
A.长为m厘米,宽为8厘米的长方形的面积
B.8件单价为m元的同款外衣的总价
C.一台每天能生产m个零件的机器,工作8天生产的零件总量
D.十位数字为8,个位数字为m的两位数
D
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
作业布置
详见教材习题
P100 T1-4
P103 T1-4
谢
谢
第三章 整式及其加减
六年级上册
1 认识代数式
第2课时 代数式
课前小测
4a
a2
(2m+0.5n)
(1)边长为a cm的正方形的周长是 cm,面积是 cm2;
(2)钢笔每支2元,铅笔每支0.5元,m支钢笔和n支铅笔共 元;
(3)温度由2 ℃下降t ℃后是 ℃。
(2-t)
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
我们知道,用字母表示数,能把数量和数量关系一般而又简明地表达出来,为研究和叙述问题带来方便.请同学完成下面的问题:
(1)正方体的边长为a,则正方体的体积为 ;
(2)x的4倍与3的差可以表示为 ;
(3)汽车上有a名乘客,中途下去b名,又上来c名,现在车上有 名乘客;
(4)圆的半径用r表示,它的周长是 ,面积是 ;
(5)一辆汽车t小时行驶了s千米,则汽车的速度为 千米/时.
a3
4x-3
(a-b+c)
2πr
πr2
新知初探
贰
合作探究
探究活动1 代数式的意义
观察 思考
上面各问题中得到的含有字母的式子,你发现它们包含哪些运算?与同伴交流.
a3
4x-3
(a-b+c)
2πr
πr2
归纳小结
像上面这些式子,除了含有数字或表示数的字母之外,通常还含有运算符号(加、减、乘、除、乘方、开方),这样的式子都是代数式.
单独一个数或一个字母也是代数式.
温馨提示:(1)代数式中不含“=”“>”“<”“≠”等符号.
(2)代数式可以简明地描述许多实际问题中的数量关系.
典例分析
阅读·思考:教材第100页“代数”的由来.
例1 设字母a表示甲数,字母b表示乙数,用代数式表示:
(1)甲、乙两数的差的2倍;
(2)甲数的 与乙数的 的差;
(3)甲、乙两数的差的立方;
(4)甲、乙两数的平方和.
解:(1)2(a-b); (2) a- b;
(3)(a-b)3; (4)a2+b2.
归纳小结
1.在把文字叙述的语句“翻译”成代数式时,首先要正确理解这一语句的数学含义;同时,要正确判断语句中所给出的各种运算的顺序.
2.代数式的书写格式要求:
(1)字母与字母相乘,乘号通常写作“ ”或省略不写,如v×t写成v t或vt,而数字与数字相乘仍用“×”号;
(2)数字与字母相乘,数字应写在字母前面,如a×3=3a;
(3)带分数与字母相乘时,应先把带分数化成假分数后再与字母相乘,如 2 ×a= a;
(4)除法运算一般写成分数形式,如s÷v应写为 ;
(5)在一些实际问题中,所列式子是积或商的形式,把单位名称直接写在后面,若是和或差的形式则必须把式子用括号括起来,再将单位名称写在式子的后面,如ab厘米、(a+b)千克等.
合作探究
针对训练:教材第99页随堂练习第1,2题.
例2 与文字语言叙述下列代数式:
(1)x+y;(2) (x-y);(3)(x+y)2;(4)x3+y3.
解:(1)x与y两数的和;(2)x与y两数差的 ;
(3)x与y两数和的平方;(4)x与y两数的立方和.
归纳小结:用语言表达代数式的意义,一定要正确判断代数式中含有的各种运算及其顺序,要以不引起误解为前提,灵活运用和、差、积、商、倍、倒数等词语.
合作探究
探究活动2 代数式的实际背景或几何意义
例3 甲、乙两地相距150km,一辆汽车的行驶速度为a km/h,用代数式表示:
(1)这辆汽车从甲地到乙地需要行驶多长时间?
(2)若速度增加2km/h,则需要多长时间?加速后可以早到多长时间?
解:(1)这辆汽车从甲地到乙地需要行驶 h.
(2)如果速度增加2km/h,那么行驶速度就是(a+2)km/h,所以从
甲地到乙地需要行驶 h.加速后可以早到( - )h.
合作探究
思考·交流:
代数式10x+5y可以表示哪些生活中的问题?与同伴交流.
如果用x(单位:m/s)表示小明跑步的速度,用y(单位:m/s)表示小明走路的速度,那么10x+5y表示他跑步10 s和走路5 s所经过的路程;如果用x和y分别表示1元和5角硬币的枚数,那么10x+5y就表示x枚1元硬币和y枚5角硬币共是多少角钱.
针对练习:教材第102页随堂练习第1,4题;教材第103页
习题第3题.
归纳小结
解决这类问题的关键是熟知常见问题如行程、工程、销售等问题中的数量关系,以及一些面积、体积公式,在书写代数式时,若是和或差的形式必须把式子用括号括起来,将单位名称写在式子的后面.
当堂达标
叁
当堂达标
1.下列各式:
(1)a+b=5; (2)5a-3y ; (3)2;
(4)n ; (5)2(a+b)+7; (6) ;
(7)2+7-6; (8)23; (9)x+5>3.
其中哪些是代数式,哪些不是代数式
解析:代数式是用运算符号(加、减、乘、除、乘方等)把数和字母连接而成的式子,而用“=”“≠”“<”“>”“≤”“≥”等关系符号连接而成的式子都不是代数式.
解:(2)(3)(4)(5)(6)(7)(8)是代数式,而(1)(9)不是代数式.
当堂达标
解析: 根据代数式的书写要求,不能出现带分数,故①不符合;数字与字母相乘时,乘号省略或用“ ”表示,并且数字在前,故②不符合;含有字母的除法中,一般应写成分数的形式,故③不符合.故选D.
D
2.下列各式中符合代数式书写要求的个数为 ( )
① x2y; ②y×3; ③ab÷2; ④ .
A.4 B.3 C.2 D.1
当堂达标
3.对于代数式2x-3y,下列读法不正确的有 ( )
A.2x 减去3y
B.2x与3y 的差
C.x的2倍与y 的3倍的差
D.2乘x 减去3乘y
解析: 代数式的读法有两种,一种是按运算关系读,另一种是按运算结果来读.无论哪一种,都要注意运算顺序.A,B,C的读法都可以与代数式相对应,D有可能误理解为(2x-3)y.故选D.
D
当堂达标
4.下列选项中的量不能用“8m”表示的是( )
A.长为m厘米,宽为8厘米的长方形的面积
B.8件单价为m元的同款外衣的总价
C.一台每天能生产m个零件的机器,工作8天生产的零件总量
D.十位数字为8,个位数字为m的两位数
D
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
作业布置
详见教材习题
P100 T1-4
P103 T1-4
谢
谢
同课章节目录
