3.1 认识代数式 第3课时 代数式的值 课件(共25张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册
文档属性
| 名称 | 3.1 认识代数式 第3课时 代数式的值 课件(共25张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 15:03:41 | ||
图片预览







文档简介
(共25张PPT)
第三章 整式及其加减
六年级上册
1 认识代数式
第3课时 代数式的值
1. 设x是用字母表示的有理数,则下面各式中必大于零的是( )
A.x+2 B.2x C.|x| D.x2+2
课前小测
D
C
2. 下列选项中,能用2a+6表示的是( )
A.整条线段的长度
B.整条线段的长度
C.这个长方形的周长
D.这个图形的面积
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
(1)遗传是影响一个人身高的因素之一。国外有学者总结出由父母身高预测子女身高的公式:儿子成年后的身高= ,女儿成年后的身高= ,其中a是父亲的身高,b是母亲的身高,单位是:m。现在你可以预测一下自己的身高了。
(2)你们用同一个公式计算的结果相同吗?为什么?
新知初探
贰
合作探究
探究活动1 代数式的值
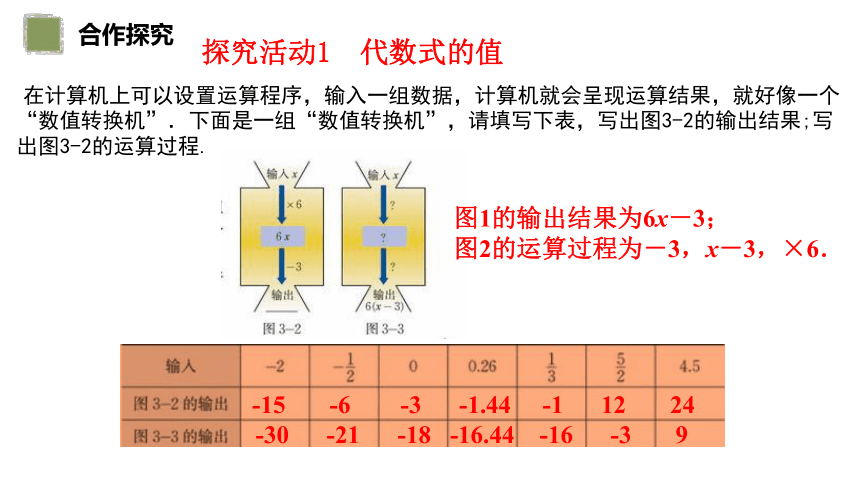
在计算机上可以设置运算程序,输入一组数据,计算机就会呈现运算结果,就好像一个“数值转换机”.下面是一组“数值转换机”,请填写下表,写出图3-2的输出结果;写出图3-2的运算过程.
图1的输出结果为6x-3;
图2的运算过程为-3,x-3,×6.
-15 -6 -3 -1.44 -1 12 24
-30 -21 -18 -16.44 -16 -3 9
归纳小结
观察 思考
在上面问题中,不管是6x-3还是6(x-3),当x取某个确定的值时,代数式的结果是否只有一个?可能是两个吗?
小结:当x的值取某个确定的数值时,利用“数值转换机”所设定的程序,就可以计算出代数式6x-3的一个结果.
一般地,用代数式代替代数式中的字母,计算所得的结果叫作代数式的值.
典例分析
[例1]当x=3,y=-2时,求代数式2x2-xy-y2的值.
针对练习:
(1)教材第105随堂练习第1,2题;
(2)教材第104页习题第3题.
解:当x=3,y=-2时,
2x2-xy-y2=2×32-3×(-2)-(-2)2=18+6-4=20.
典例分析
[例2]营养学家通常用身体质量指数(简称BMI)衡量人体胖瘦程度,这个指数等于人体体重(单位:kg)与人体身高(单位:m)平方的商.对于成年人来说,BMI在18.5与24之间,体重适中;BMI低于18.5,体重过轻;BMI高于24,体重超重.
(1)设一个人的体重为wg,身高为hm,请用含w,h的代数式表示BMI的值.
(2)张老师的身高为1.75m,体重为65g,他的体重是否适中?
(3)BMI值对未成年人的胖瘦程度也有一定参考意义,请用上面的代数式计算你的BMI值,判断自己的体重是否适中.
解:(1) ;
(2)把h=1.75,w=65代入,得 = ≈21.22.
而18.5<21.22<24,因此他的身体适中.
(3)根据自己的身高与体重计算即可.
归纳小结
代数式求值的三种类型:
(1)直接代入求值
用具体数值代替代数式中的字母,按照代数式中的运算顺序计算.
(2)整体代入求值
根据代数式的特点,整体代入求得代数式的值,一般分直接整体代入与变形后整体代入.
(3)数值转化机求值
按指定程序代入计算.
合作探究
探究活动2 利用代数式的值推断一些代数 式所反映的规律
观察 思考
填写下表,并观察5n+6和n2这两个代数式的值的变化情况.
n 1 2 3 4 5 6 7 8
5n+6
n2
(1)随着n的值逐渐变大,5n+6和n2这两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100?
11 16 21 26 31 36 41 46
1 4 9 16 25 36 49 64
随着n的值逐渐变大,5n+6和n2这两个代数式的值逐渐增大.
n2的值先超过100.
典例分析
[例3] 物体自由下落的高度h m和下落的时间t s的关系,在地球上大约是h=4.9t2,在月球上大约是h=0.8t2.
(1)填写下表:
t 0 2 4 6 8
10
h=4.9t2
h=0.8t2
(3)当h=20 m时,比较物体在地球上和月球上自由下落所需的时间.
(2)物体在哪儿下落得快
归纳小结
(1)代数式的值是按代数式的运算关系得到的具体数值,随字母取值的不同而不同,字母的值确定了,代数式的值也就确定了,但字母的取值必须确保代数式有意义.
(2)代数式中原来省略乘号时,代入具体数值后出现数与数相乘时,必须恢复乘号.
(3)若做乘方运算,字母给出的数值是负数或分数时,代入时要加括号.
(4)一个代数式的值由它所含字母的值决定,具有不唯一性.
当堂达标
叁
当堂达标
1.当x=2时,下列代数式中与代数式2x+1的值相等的是 ( )
A.1-x2 B.3x+1
C.3x-x2 D.x2+1
D
解析: 将x=2代入各代数式,得2x+1=5,
1-x2=-3,3x+1=7,3x-x2=2,x2+1=5.故选D.
当堂达标
2.如图所示的图形的面积用代数式表示
是 ( )
A.ab+bc
B.c[b-d+d(a-c)]
C.ad+c(b-d)
D.ab-cd
解析:把图形看成一个大的长方形,面积为ab,再减去长为d,宽为c的长方形的面积,剩下的就是所求图形的面积,即ab-cd.故选D.
D
当堂达标
3.当m=3,n=-2时,代数式m2-2n2的值是 .
解析: 将m=3,n=-2代入m2-2n2得9-2×(-2)2=1.故填1.
1
当堂达标
4.代数式x2+x+3的值为7,则代数式
2x2+2x-3的值为 .
解析: 由x2+x+3=7可知x2+x=4,所以2x2+2x-3=2(x2+x)-3
=2×4-3=5.故填5.
当堂达标
5.有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2024次输出的结果是 .
输入x
x为奇数
x为偶数
x+3
输出
当堂达标
解析:首先由数值转换器发现第二次输出的结果是4,为偶数,所以第三次输出的结果为2,第四次为1,第五次为4,第六次为2,…,可得出规律:从第二次开始,每三次一个循环.因为(2024-1)÷3=674……1,所以第2024次输出的结果是4.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
1.代数式求值步骤:
求代数式的值时,先确定是直接代入还是整体代入,然后按照运算顺序进行计算.
2.如何列代数式
列代数式时,要善于抓住关键性的词语,如“大、小、多、少、增加、减少、和、差、积、商”等,还要注意已知量和未知量之间的关系.
作业布置
详见教材习题
P106-107 T1-7
谢
谢
第三章 整式及其加减
六年级上册
1 认识代数式
第3课时 代数式的值
1. 设x是用字母表示的有理数,则下面各式中必大于零的是( )
A.x+2 B.2x C.|x| D.x2+2
课前小测
D
C
2. 下列选项中,能用2a+6表示的是( )
A.整条线段的长度
B.整条线段的长度
C.这个长方形的周长
D.这个图形的面积
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
(1)遗传是影响一个人身高的因素之一。国外有学者总结出由父母身高预测子女身高的公式:儿子成年后的身高= ,女儿成年后的身高= ,其中a是父亲的身高,b是母亲的身高,单位是:m。现在你可以预测一下自己的身高了。
(2)你们用同一个公式计算的结果相同吗?为什么?
新知初探
贰
合作探究
探究活动1 代数式的值
在计算机上可以设置运算程序,输入一组数据,计算机就会呈现运算结果,就好像一个“数值转换机”.下面是一组“数值转换机”,请填写下表,写出图3-2的输出结果;写出图3-2的运算过程.
图1的输出结果为6x-3;
图2的运算过程为-3,x-3,×6.
-15 -6 -3 -1.44 -1 12 24
-30 -21 -18 -16.44 -16 -3 9
归纳小结
观察 思考
在上面问题中,不管是6x-3还是6(x-3),当x取某个确定的值时,代数式的结果是否只有一个?可能是两个吗?
小结:当x的值取某个确定的数值时,利用“数值转换机”所设定的程序,就可以计算出代数式6x-3的一个结果.
一般地,用代数式代替代数式中的字母,计算所得的结果叫作代数式的值.
典例分析
[例1]当x=3,y=-2时,求代数式2x2-xy-y2的值.
针对练习:
(1)教材第105随堂练习第1,2题;
(2)教材第104页习题第3题.
解:当x=3,y=-2时,
2x2-xy-y2=2×32-3×(-2)-(-2)2=18+6-4=20.
典例分析
[例2]营养学家通常用身体质量指数(简称BMI)衡量人体胖瘦程度,这个指数等于人体体重(单位:kg)与人体身高(单位:m)平方的商.对于成年人来说,BMI在18.5与24之间,体重适中;BMI低于18.5,体重过轻;BMI高于24,体重超重.
(1)设一个人的体重为wg,身高为hm,请用含w,h的代数式表示BMI的值.
(2)张老师的身高为1.75m,体重为65g,他的体重是否适中?
(3)BMI值对未成年人的胖瘦程度也有一定参考意义,请用上面的代数式计算你的BMI值,判断自己的体重是否适中.
解:(1) ;
(2)把h=1.75,w=65代入,得 = ≈21.22.
而18.5<21.22<24,因此他的身体适中.
(3)根据自己的身高与体重计算即可.
归纳小结
代数式求值的三种类型:
(1)直接代入求值
用具体数值代替代数式中的字母,按照代数式中的运算顺序计算.
(2)整体代入求值
根据代数式的特点,整体代入求得代数式的值,一般分直接整体代入与变形后整体代入.
(3)数值转化机求值
按指定程序代入计算.
合作探究
探究活动2 利用代数式的值推断一些代数 式所反映的规律
观察 思考
填写下表,并观察5n+6和n2这两个代数式的值的变化情况.
n 1 2 3 4 5 6 7 8
5n+6
n2
(1)随着n的值逐渐变大,5n+6和n2这两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100?
11 16 21 26 31 36 41 46
1 4 9 16 25 36 49 64
随着n的值逐渐变大,5n+6和n2这两个代数式的值逐渐增大.
n2的值先超过100.
典例分析
[例3] 物体自由下落的高度h m和下落的时间t s的关系,在地球上大约是h=4.9t2,在月球上大约是h=0.8t2.
(1)填写下表:
t 0 2 4 6 8
10
h=4.9t2
h=0.8t2
(3)当h=20 m时,比较物体在地球上和月球上自由下落所需的时间.
(2)物体在哪儿下落得快
归纳小结
(1)代数式的值是按代数式的运算关系得到的具体数值,随字母取值的不同而不同,字母的值确定了,代数式的值也就确定了,但字母的取值必须确保代数式有意义.
(2)代数式中原来省略乘号时,代入具体数值后出现数与数相乘时,必须恢复乘号.
(3)若做乘方运算,字母给出的数值是负数或分数时,代入时要加括号.
(4)一个代数式的值由它所含字母的值决定,具有不唯一性.
当堂达标
叁
当堂达标
1.当x=2时,下列代数式中与代数式2x+1的值相等的是 ( )
A.1-x2 B.3x+1
C.3x-x2 D.x2+1
D
解析: 将x=2代入各代数式,得2x+1=5,
1-x2=-3,3x+1=7,3x-x2=2,x2+1=5.故选D.
当堂达标
2.如图所示的图形的面积用代数式表示
是 ( )
A.ab+bc
B.c[b-d+d(a-c)]
C.ad+c(b-d)
D.ab-cd
解析:把图形看成一个大的长方形,面积为ab,再减去长为d,宽为c的长方形的面积,剩下的就是所求图形的面积,即ab-cd.故选D.
D
当堂达标
3.当m=3,n=-2时,代数式m2-2n2的值是 .
解析: 将m=3,n=-2代入m2-2n2得9-2×(-2)2=1.故填1.
1
当堂达标
4.代数式x2+x+3的值为7,则代数式
2x2+2x-3的值为 .
解析: 由x2+x+3=7可知x2+x=4,所以2x2+2x-3=2(x2+x)-3
=2×4-3=5.故填5.
当堂达标
5.有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2024次输出的结果是 .
输入x
x为奇数
x为偶数
x+3
输出
当堂达标
解析:首先由数值转换器发现第二次输出的结果是4,为偶数,所以第三次输出的结果为2,第四次为1,第五次为4,第六次为2,…,可得出规律:从第二次开始,每三次一个循环.因为(2024-1)÷3=674……1,所以第2024次输出的结果是4.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
1.代数式求值步骤:
求代数式的值时,先确定是直接代入还是整体代入,然后按照运算顺序进行计算.
2.如何列代数式
列代数式时,要善于抓住关键性的词语,如“大、小、多、少、增加、减少、和、差、积、商”等,还要注意已知量和未知量之间的关系.
作业布置
详见教材习题
P106-107 T1-7
谢
谢
同课章节目录
