3.3 探索与表达规律 课件(共36张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册
文档属性
| 名称 | 3.3 探索与表达规律 课件(共36张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 15:08:33 | ||
图片预览





文档简介
(共36张PPT)
第三章 整式及其加减
六年级上册
3 探索与表达规律
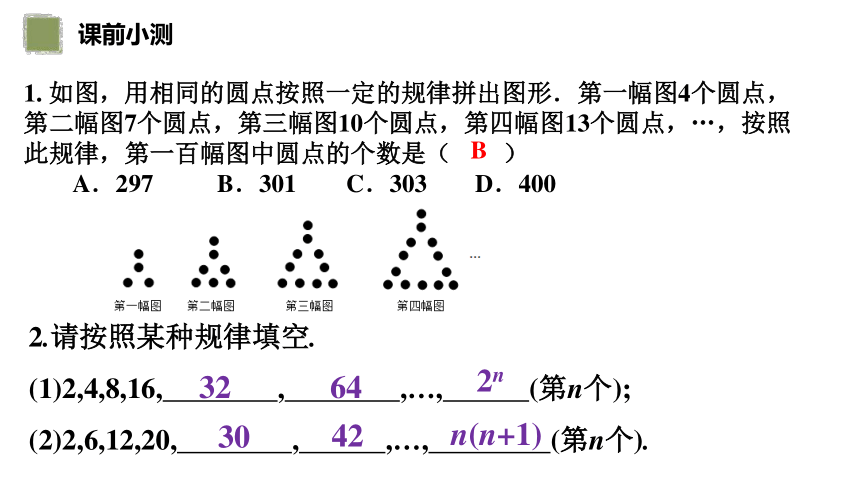
1. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点,…,按照此规律,第一百幅图中圆点的个数是( )
A.297 B.301 C.303 D.400
课前小测
B
2.请按照某种规律填空.
(1)2,4,8,16, , ,…, (第n个);
(2)2,6,12,20, , ,…, (第n个).
32
2n
64
30
n(n+1)
42
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
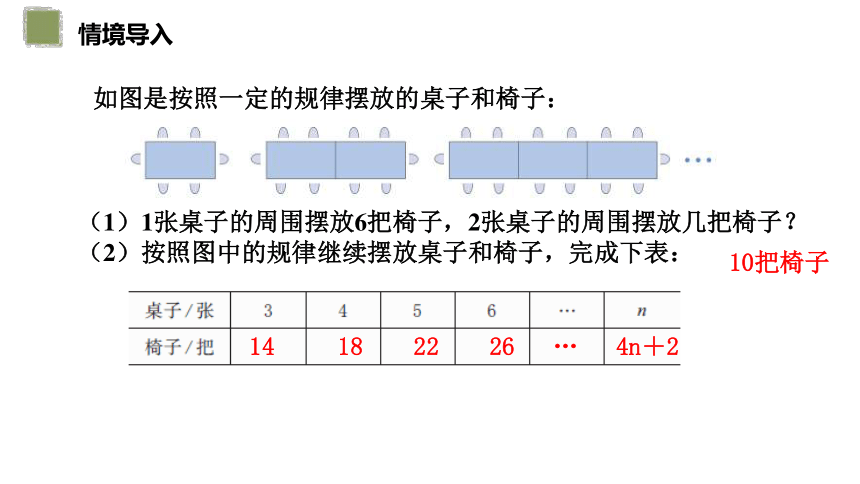
如图是按照一定的规律摆放的桌子和椅子:
(1)1张桌子的周围摆放6把椅子,2张桌子的周围摆放几把椅子?
(2)按照图中的规律继续摆放桌子和椅子,完成下表:
10把椅子
14 18 22 26 … 4n+2
新知初探
贰
合作探究
探究活动1 图形规律探索
尝试·交流
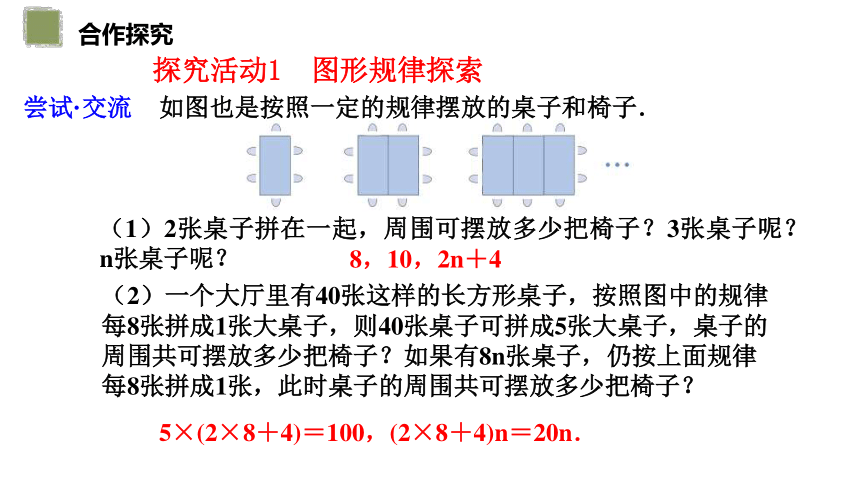
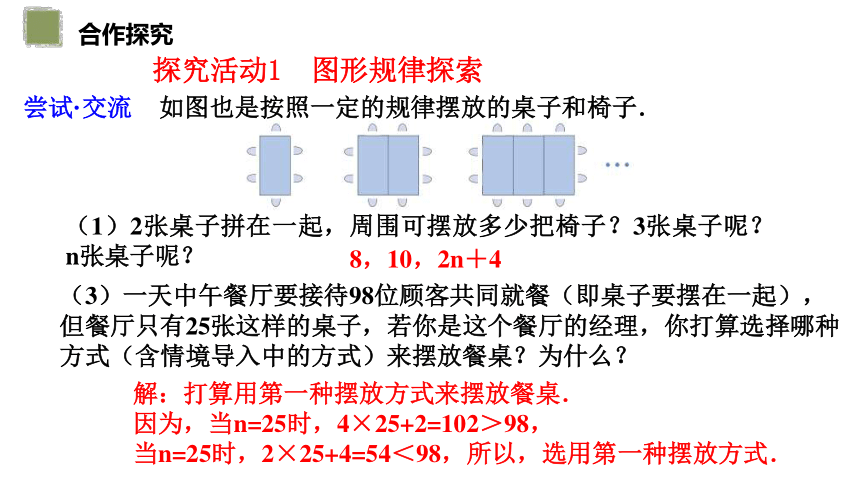
如图也是按照一定的规律摆放的桌子和椅子.
(1)2张桌子拼在一起,周围可摆放多少把椅子?3张桌子呢?n张桌子呢?
8,10,2n+4
(2)一个大厅里有40张这样的长方形桌子,按照图中的规律每8张拼成1张大桌子,则40张桌子可拼成5张大桌子,桌子的周围共可摆放多少把椅子?如果有8n张桌子,仍按上面规律每8张拼成1张,此时桌子的周围共可摆放多少把椅子?
5×(2×8+4)=100,(2×8+4)n=20n.
合作探究
探究活动1 图形规律探索
尝试·交流
如图也是按照一定的规律摆放的桌子和椅子.
(1)2张桌子拼在一起,周围可摆放多少把椅子?3张桌子呢?n张桌子呢?
8,10,2n+4
(3)一天中午餐厅要接待98位顾客共同就餐(即桌子要摆在一起),但餐厅只有25张这样的桌子,若你是这个餐厅的经理,你打算选择哪种方式(含情境导入中的方式)来摆放餐桌?为什么?
解:打算用第一种摆放方式来摆放餐桌.
因为,当n=25时,4×25+2=102>98,
当n=25时,2×25+4=54<98,所以,选用第一种摆放方式.
合作探究
(1)小明也用上面的8张桌子拼成1张大桌子,但8n张桌子的周围只能摆放16n把椅子,你能说出他的桌子是怎么摆放的吗
(2)若仍用上面的桌子,每8张桌子拼成1张大桌子,你还有其他摆放桌子的方法吗?按照你的摆放方法,8n张桌子的周围共可摆放多少把椅子?
(3)在食堂就餐的高峰时段,需要同时能坐下300人,选择上面哪种方式需要的餐桌数较少?
解:(1)如图所示;
尝试·思考
(2)如图所示;
(3)第(2)种方式.
归纳小结
1.探索规律是从具体的、特殊的、简单的问题出发,观察各个数量的特点以及相互之间的变化规律.
2.探索规律一般要经历以下的一些过程:
(1)观察它前后几项的和、差、积、商和乘方等特点,注意数的大小、结构的变化、图形位置的变换,进行多角度的观察与调整;
(2)从已知的有限个数据或图形中去寻找数量关系和图形之间的关系,并进行归纳;
(3)从归纳出的数量关系或图形关系进行大胆的猜测,得出他们共同的规律;
(4)列举符合条件的数据和图形,验证猜想的规律的正确性,得出结论.
合作探究
探究活动2 日历中的规律
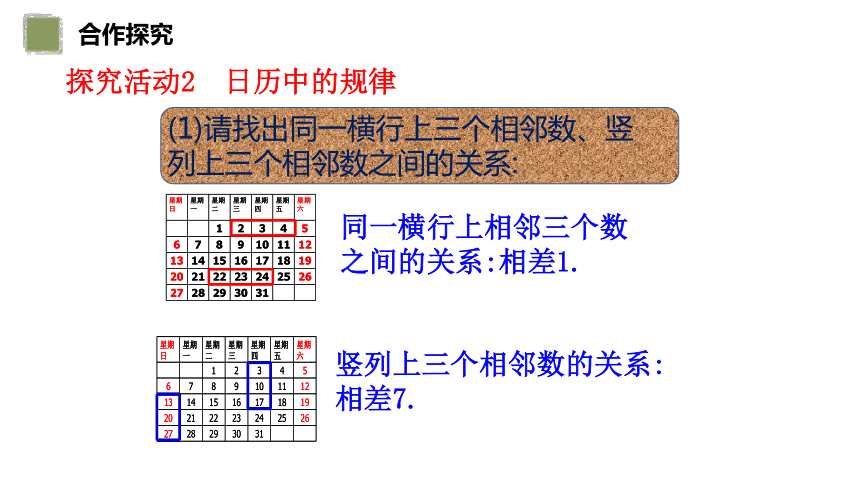
(1)请找出同一横行上三个相邻数、竖
列上三个相邻数之间的关系:
同一横行上相邻三个数之间的关系:相差1.
竖列上三个相邻数的关系:相差7.
合作探究
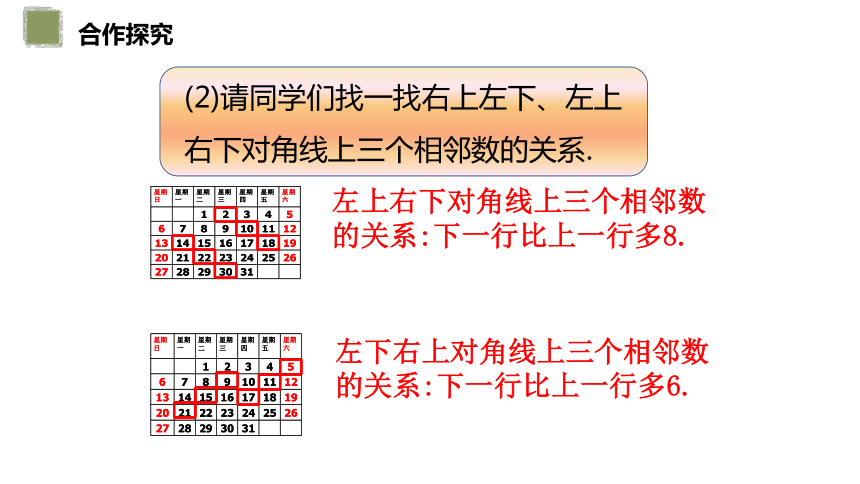
(2)请同学们找一找右上左下、左上右下对角线上三个相邻数的关系.
左上右下对角线上三个相邻数的关系:下一行比上一行多8.
左下右上对角线上三个相邻数的关系:下一行比上一行多6.
合作探究
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系
(2)这个关系对其他这样的方框成立吗 你能用代数式表示这个关系吗
思考
合作探究
(3)这个关系对任何一个月的日历都成立吗 为什么
(4)你还能发现这样的方框中9个数之间的其他关系吗 用代数式表示.
合作探究
通过表格可以很快地解决方框中9个数之间的关系:9个数的和是中间这个数的9倍.
a-8 a-7
a-6
a-1 a
a+1
a+6 a+7
a+8
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+
(a+7)+(a+8)=9a.
合作探究
尝试·思考
(1)上面的日历图中,能否使框中9个数的和为144?180呢?
解:144÷9=16,所以上面日历图中能使框中9个数的和为144,中间的数为16;
180÷9=20,但上面日历图中20在最左边,所以不能使框中9个数的和为180.
合作探究
尝试·思考
(2)在某个月的日历中,恰好有五个星期日位于同一列且日期数的和为80,这个月的第一个星期日是几号?
解:设中间一个星期日为a号,则a-14+a-7+a+a+7+a+14=5a=80,所以a=16,16-14=2(号),即这个月的第一个星期日是2号.
合作探究
(1)如果将方框改为十字形框,你能发现哪些规律 如果改为H形框呢
(2)你还能设计其他形状的包含数字规律的数框吗
“十”字形:5个数的和是中间这个数的5倍;
“H” 形:7个数的和是中间这个数的7倍;
设计的其他形状的方框为“M”形框,而“M”形与“H”形一样,7个数的和是中间这个数的7倍.
思考·交流
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a-14
a-7
a
a+7
a+14
还有其他规律吗?
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a a+1
a+7 a+8
还有其他规律吗?
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a a+1 a+2 a+3
a+7 a+8 a+9 a+10
a+14 a+15 a+16 a+17
a+21 a+22 a+23 a+24
还有其他规律吗?
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a a+3
a+8 a+9
a+15 a+16
a+21 a+24
还有其他规律吗?
归纳小结
在日历图中,每一行上相邻两个数字间相差1,每一列上相邻两个数字间相差7,解答该类问题一般设中间的数字是a,然后列代数式表示其他数字,解决问题,注意所求中间的数字不能在上下左右四条边上.
合作探究
探究活动3 数字规律探索
合作·交流
小亮和小丽在玩一个数字游戏.
你知道小亮是怎样算出来的吗?
归纳小结
解答:设小亮想好的两位数个位数字和十位数字分别是a和b,按照运算步骤,最后结果为10b+15+a,因此只要把计算结果减去15,得到的数就是小亮想好的两位数.
文字语言
符号语言
用代数式表示
代数式的意义
1.探索规律的基本方法:
分析数量关系 列代数式表示 验证结论
2.探索规律的基本思想:特殊 一般.
典例分析
例(1)一个三位数能否被3整除,只要看这个数的各数位上的数字之和能否被3整除.你能说明其中的道理吗?
解析:设这个三位数为100a+10b+c,则100a+10b+c=99a+9b+(a+b+c),因为99a和9b都能被3整除,若a+b+c也能被3整除,则100a+10b+c就是3的倍数,即该三位数可以被3整除,所以一个三位数能不能被3整除,只要看这个数的各位上数字之和能不能被3整除即可.
(2)一个四位数能否被3整除是否也有这样的规律?请说明理由.
解析:设这个三位数为1000a+100b+10c+d,则1000a+100b+10c+d=999a+99b+9c+(a+b+c+d),因为999a,99b和9c都能被3整除,若a+b+c+d也能被3整除,则1000a+100b+10c+d就是3的倍数,即该四位数可以被3整除,所以一个四位数能不能被3整除,只要看这个数的各位上数字之和能不能被3整除即可.
合作探究
自主设计游戏
预设:小组1:我们由1号学生随便想一个两位数,将十位数字加上5,然后乘10,再减去50,再加上个位数字,最后将结果告诉我们,我们就知道1号学生心里想的两位数了,结果还是原数.
原理:用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为10a+b,则10(a+5)-50+b=10a+50-50+b=10a+b.
合作探究
小组2:我们是由1号学生随便想一个数,并将此数字乘2加3,然后乘5减5,再除以10,最后告诉我们结果,我们很轻松就知道同伴所想的数了,结果比原数大1.
原理: 用a表示这个数,则
[5(2a+3)-5]÷10=(10a+15-5)÷10
=(10a+10)÷10=a+1.
合作探究
小组3:我们设计的是猜电话号码游戏,1,2位的数字所形成的两位数比3的4倍多1;3,4位的数字所形成的两位数比9的4倍多1;5,6,7位的数字依次是6,3,7;8位的数字是最小的自然数;9,10,11位的数字所形成的三位数比600多26.结果大家很容易猜出来是13376370626.
原理: 1,2位的数字所形成的两位数是3×4+1=13;3,4位的数字所形成的两位数是9×4+1=37;5,6,7位的数字依次是6,3,7;8位的数字是最小的自然数0;9,10,11位的数字所形成的三位数是600+26=626.故结果是13376370626.
当堂达标
叁
当堂达标
1. 如图是用黑色棋子摆放而成的图案,其中第①个图中有3枚棋子,第②个图中有6枚棋子,第③个图中有11枚棋子,第④个图中有18枚棋子……按此规律,第⑦个图案黑色棋子的个数为( )
A.36 B.49 C.51 D.65
2. 如图,填在下面每个正方形中的四个数之间都有相同的规律,按照这种规律排列,最后一个正方形中m的值是 .
158
C
当堂达标
3.在如图所示的日历中,任意圈起右斜对的4个数.
(1)你发现这4个数之间有什么关系?
(2)若设最小的一个数是a,则其余3个数如何表示?它们的和是多少?它们的和能被4整除吗?
(3)若任意圈起左斜对的4个数,你发现这4个数之间又有什么关系?若设最小的一个数是b,其余3个数如何表示?
解:(1)发现相邻两数相差8.
(2)设最小的一个数是a,则其他数为:a+8、a+16、a+24.
a+(a+8)+(a+16)+(a+24)=4a+48
对4a+48提取公因数可得4(a+12),所以这4个数的和能被4整除.
(3)若任意圈起左斜对的4个数,通过观察圈起来的4个数,可发现相邻两数相差6,若设最小的一个数是b,则其余3个数分别为:b+6、b+12、b+18.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
探索规律的一般步骤
观察特例寻找数量关系
大胆猜想规律
用代数式表示规律
验证规律是否成立
得出结论
成立
不
成
立
作业布置
详见教材习题
P128 T1-3
P131 T1-4
谢
谢
第三章 整式及其加减
六年级上册
3 探索与表达规律
1. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点,…,按照此规律,第一百幅图中圆点的个数是( )
A.297 B.301 C.303 D.400
课前小测
B
2.请按照某种规律填空.
(1)2,4,8,16, , ,…, (第n个);
(2)2,6,12,20, , ,…, (第n个).
32
2n
64
30
n(n+1)
42
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
如图是按照一定的规律摆放的桌子和椅子:
(1)1张桌子的周围摆放6把椅子,2张桌子的周围摆放几把椅子?
(2)按照图中的规律继续摆放桌子和椅子,完成下表:
10把椅子
14 18 22 26 … 4n+2
新知初探
贰
合作探究
探究活动1 图形规律探索
尝试·交流
如图也是按照一定的规律摆放的桌子和椅子.
(1)2张桌子拼在一起,周围可摆放多少把椅子?3张桌子呢?n张桌子呢?
8,10,2n+4
(2)一个大厅里有40张这样的长方形桌子,按照图中的规律每8张拼成1张大桌子,则40张桌子可拼成5张大桌子,桌子的周围共可摆放多少把椅子?如果有8n张桌子,仍按上面规律每8张拼成1张,此时桌子的周围共可摆放多少把椅子?
5×(2×8+4)=100,(2×8+4)n=20n.
合作探究
探究活动1 图形规律探索
尝试·交流
如图也是按照一定的规律摆放的桌子和椅子.
(1)2张桌子拼在一起,周围可摆放多少把椅子?3张桌子呢?n张桌子呢?
8,10,2n+4
(3)一天中午餐厅要接待98位顾客共同就餐(即桌子要摆在一起),但餐厅只有25张这样的桌子,若你是这个餐厅的经理,你打算选择哪种方式(含情境导入中的方式)来摆放餐桌?为什么?
解:打算用第一种摆放方式来摆放餐桌.
因为,当n=25时,4×25+2=102>98,
当n=25时,2×25+4=54<98,所以,选用第一种摆放方式.
合作探究
(1)小明也用上面的8张桌子拼成1张大桌子,但8n张桌子的周围只能摆放16n把椅子,你能说出他的桌子是怎么摆放的吗
(2)若仍用上面的桌子,每8张桌子拼成1张大桌子,你还有其他摆放桌子的方法吗?按照你的摆放方法,8n张桌子的周围共可摆放多少把椅子?
(3)在食堂就餐的高峰时段,需要同时能坐下300人,选择上面哪种方式需要的餐桌数较少?
解:(1)如图所示;
尝试·思考
(2)如图所示;
(3)第(2)种方式.
归纳小结
1.探索规律是从具体的、特殊的、简单的问题出发,观察各个数量的特点以及相互之间的变化规律.
2.探索规律一般要经历以下的一些过程:
(1)观察它前后几项的和、差、积、商和乘方等特点,注意数的大小、结构的变化、图形位置的变换,进行多角度的观察与调整;
(2)从已知的有限个数据或图形中去寻找数量关系和图形之间的关系,并进行归纳;
(3)从归纳出的数量关系或图形关系进行大胆的猜测,得出他们共同的规律;
(4)列举符合条件的数据和图形,验证猜想的规律的正确性,得出结论.
合作探究
探究活动2 日历中的规律
(1)请找出同一横行上三个相邻数、竖
列上三个相邻数之间的关系:
同一横行上相邻三个数之间的关系:相差1.
竖列上三个相邻数的关系:相差7.
合作探究
(2)请同学们找一找右上左下、左上右下对角线上三个相邻数的关系.
左上右下对角线上三个相邻数的关系:下一行比上一行多8.
左下右上对角线上三个相邻数的关系:下一行比上一行多6.
合作探究
(1)日历图的套色方框中的9个数之和与该方框正中间的数有什么关系
(2)这个关系对其他这样的方框成立吗 你能用代数式表示这个关系吗
思考
合作探究
(3)这个关系对任何一个月的日历都成立吗 为什么
(4)你还能发现这样的方框中9个数之间的其他关系吗 用代数式表示.
合作探究
通过表格可以很快地解决方框中9个数之间的关系:9个数的和是中间这个数的9倍.
a-8 a-7
a-6
a-1 a
a+1
a+6 a+7
a+8
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+
(a+7)+(a+8)=9a.
合作探究
尝试·思考
(1)上面的日历图中,能否使框中9个数的和为144?180呢?
解:144÷9=16,所以上面日历图中能使框中9个数的和为144,中间的数为16;
180÷9=20,但上面日历图中20在最左边,所以不能使框中9个数的和为180.
合作探究
尝试·思考
(2)在某个月的日历中,恰好有五个星期日位于同一列且日期数的和为80,这个月的第一个星期日是几号?
解:设中间一个星期日为a号,则a-14+a-7+a+a+7+a+14=5a=80,所以a=16,16-14=2(号),即这个月的第一个星期日是2号.
合作探究
(1)如果将方框改为十字形框,你能发现哪些规律 如果改为H形框呢
(2)你还能设计其他形状的包含数字规律的数框吗
“十”字形:5个数的和是中间这个数的5倍;
“H” 形:7个数的和是中间这个数的7倍;
设计的其他形状的方框为“M”形框,而“M”形与“H”形一样,7个数的和是中间这个数的7倍.
思考·交流
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a-14
a-7
a
a+7
a+14
还有其他规律吗?
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a a+1
a+7 a+8
还有其他规律吗?
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a a+1 a+2 a+3
a+7 a+8 a+9 a+10
a+14 a+15 a+16 a+17
a+21 a+22 a+23 a+24
还有其他规律吗?
合作探究
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
a a+3
a+8 a+9
a+15 a+16
a+21 a+24
还有其他规律吗?
归纳小结
在日历图中,每一行上相邻两个数字间相差1,每一列上相邻两个数字间相差7,解答该类问题一般设中间的数字是a,然后列代数式表示其他数字,解决问题,注意所求中间的数字不能在上下左右四条边上.
合作探究
探究活动3 数字规律探索
合作·交流
小亮和小丽在玩一个数字游戏.
你知道小亮是怎样算出来的吗?
归纳小结
解答:设小亮想好的两位数个位数字和十位数字分别是a和b,按照运算步骤,最后结果为10b+15+a,因此只要把计算结果减去15,得到的数就是小亮想好的两位数.
文字语言
符号语言
用代数式表示
代数式的意义
1.探索规律的基本方法:
分析数量关系 列代数式表示 验证结论
2.探索规律的基本思想:特殊 一般.
典例分析
例(1)一个三位数能否被3整除,只要看这个数的各数位上的数字之和能否被3整除.你能说明其中的道理吗?
解析:设这个三位数为100a+10b+c,则100a+10b+c=99a+9b+(a+b+c),因为99a和9b都能被3整除,若a+b+c也能被3整除,则100a+10b+c就是3的倍数,即该三位数可以被3整除,所以一个三位数能不能被3整除,只要看这个数的各位上数字之和能不能被3整除即可.
(2)一个四位数能否被3整除是否也有这样的规律?请说明理由.
解析:设这个三位数为1000a+100b+10c+d,则1000a+100b+10c+d=999a+99b+9c+(a+b+c+d),因为999a,99b和9c都能被3整除,若a+b+c+d也能被3整除,则1000a+100b+10c+d就是3的倍数,即该四位数可以被3整除,所以一个四位数能不能被3整除,只要看这个数的各位上数字之和能不能被3整除即可.
合作探究
自主设计游戏
预设:小组1:我们由1号学生随便想一个两位数,将十位数字加上5,然后乘10,再减去50,再加上个位数字,最后将结果告诉我们,我们就知道1号学生心里想的两位数了,结果还是原数.
原理:用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为10a+b,则10(a+5)-50+b=10a+50-50+b=10a+b.
合作探究
小组2:我们是由1号学生随便想一个数,并将此数字乘2加3,然后乘5减5,再除以10,最后告诉我们结果,我们很轻松就知道同伴所想的数了,结果比原数大1.
原理: 用a表示这个数,则
[5(2a+3)-5]÷10=(10a+15-5)÷10
=(10a+10)÷10=a+1.
合作探究
小组3:我们设计的是猜电话号码游戏,1,2位的数字所形成的两位数比3的4倍多1;3,4位的数字所形成的两位数比9的4倍多1;5,6,7位的数字依次是6,3,7;8位的数字是最小的自然数;9,10,11位的数字所形成的三位数比600多26.结果大家很容易猜出来是13376370626.
原理: 1,2位的数字所形成的两位数是3×4+1=13;3,4位的数字所形成的两位数是9×4+1=37;5,6,7位的数字依次是6,3,7;8位的数字是最小的自然数0;9,10,11位的数字所形成的三位数是600+26=626.故结果是13376370626.
当堂达标
叁
当堂达标
1. 如图是用黑色棋子摆放而成的图案,其中第①个图中有3枚棋子,第②个图中有6枚棋子,第③个图中有11枚棋子,第④个图中有18枚棋子……按此规律,第⑦个图案黑色棋子的个数为( )
A.36 B.49 C.51 D.65
2. 如图,填在下面每个正方形中的四个数之间都有相同的规律,按照这种规律排列,最后一个正方形中m的值是 .
158
C
当堂达标
3.在如图所示的日历中,任意圈起右斜对的4个数.
(1)你发现这4个数之间有什么关系?
(2)若设最小的一个数是a,则其余3个数如何表示?它们的和是多少?它们的和能被4整除吗?
(3)若任意圈起左斜对的4个数,你发现这4个数之间又有什么关系?若设最小的一个数是b,其余3个数如何表示?
解:(1)发现相邻两数相差8.
(2)设最小的一个数是a,则其他数为:a+8、a+16、a+24.
a+(a+8)+(a+16)+(a+24)=4a+48
对4a+48提取公因数可得4(a+12),所以这4个数的和能被4整除.
(3)若任意圈起左斜对的4个数,通过观察圈起来的4个数,可发现相邻两数相差6,若设最小的一个数是b,则其余3个数分别为:b+6、b+12、b+18.
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
探索规律的一般步骤
观察特例寻找数量关系
大胆猜想规律
用代数式表示规律
验证规律是否成立
得出结论
成立
不
成
立
作业布置
详见教材习题
P128 T1-3
P131 T1-4
谢
谢
同课章节目录
