第三章 整式及其加减:问题解决策略:归纳 课件 (21张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册
文档属性
| 名称 | 第三章 整式及其加减:问题解决策略:归纳 课件 (21张PPT)2025-2026学年数学鲁教版(五四制)(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 21:20:08 | ||
图片预览






文档简介
(共21张PPT)
第三章 整式及其加减
六年级上册
问题解决策略:归纳
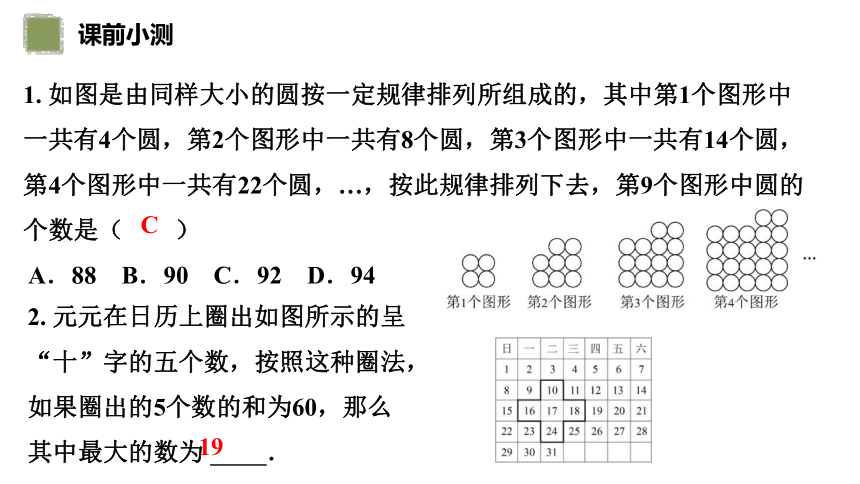
1. 如图是由同样大小的圆按一定规律排列所组成的,其中第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆,…,按此规律排列下去,第9个图形中圆的个数是( )
A.88 B.90 C.92 D.94
课前小测
19
2. 元元在日历上圈出如图所示的呈“十”字的五个数,按照这种圈法,如果圈出的5个数的和为60,那么其中最大的数为 .
C
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
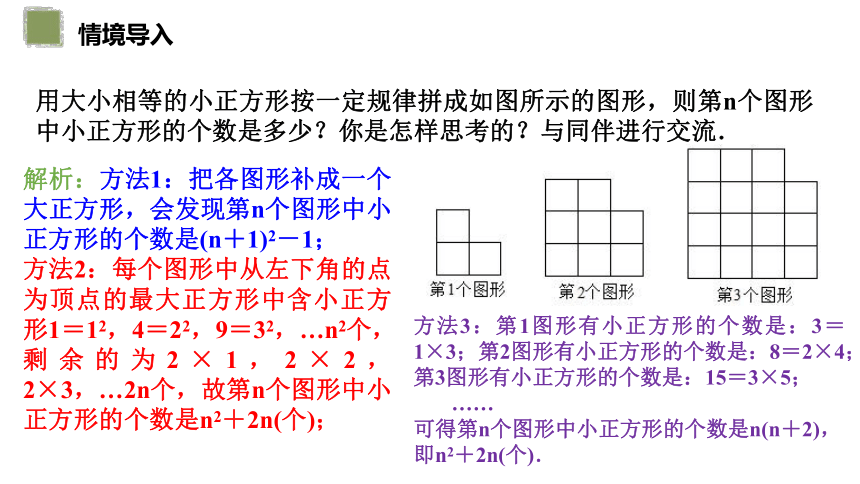
用大小相等的小正方形按一定规律拼成如图所示的图形,则第n个图形中小正方形的个数是多少?你是怎样思考的?与同伴进行交流.
解析:方法1:把各图形补成一个大正方形,会发现第n个图形中小正方形的个数是(n+1)2-1;
方法2:每个图形中从左下角的点为顶点的最大正方形中含小正方形1=12,4=22,9=32,…n2个,剩余的为2×1,2×2,2×3,…2n个,故第n个图形中小正方形的个数是n2+2n(个);
方法3:第1图形有小正方形的个数是:3=1×3;第2图形有小正方形的个数是:8=2×4;第3图形有小正方形的个数是:15=3×5;
……
可得第n个图形中小正方形的个数是n(n+2),即n2+2n(个).
新知初探
贰
合作探究
探究活动 用归纳的策略解决问题
问题 “低多边形风格”是一种数字艺术设计风格.它将整个区域分割为若干三角形,通过把相邻三角形涂上不同颜色,产生立体及光影的效果.随着三角形数量增加,效果更为斑斓绚丽(如图).
合作探究
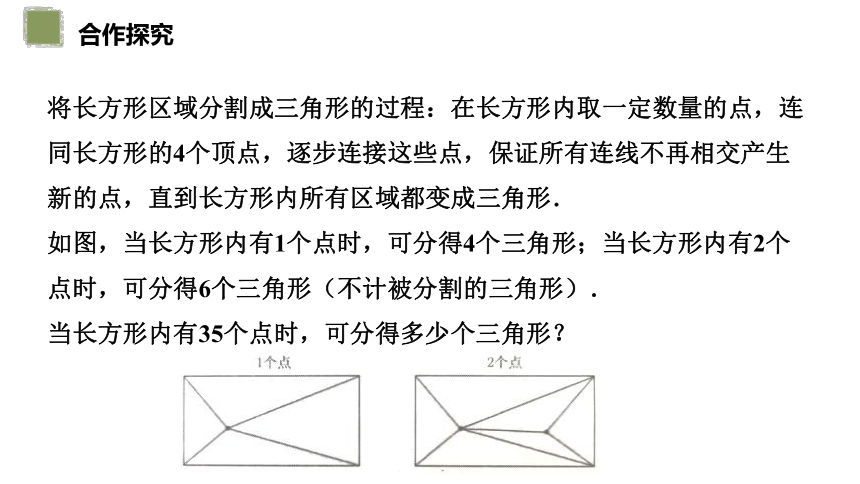
将长方形区域分割成三角形的过程:在长方形内取一定数量的点,连同长方形的4个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到长方形内所有区域都变成三角形.
如图,当长方形内有1个点时,可分得4个三角形;当长方形内有2个点时,可分得6个三角形(不计被分割的三角形).
当长方形内有35个点时,可分得多少个三角形?
合作探究
理解问题
(1)先动手画一画,感受分割得到三角形的过程.
答案不唯一,如图.
(2)已知条件是什么?目标是什么?
已知条件是在一个长方形内有一定数量的点,以及长方形的顶点,逐步连接这些点(保持所连线不再相交产生新的点)能分得一定数量的三角形.
目标是求当长方形内有35个点时,可分得三角形的个数.
合作探究
拟定计划
(1)直接研究“长方形内有35个点”的情形,你遇到了什么困难?
画出“长方形内有35个点”分三角形的情形比较繁琐、复杂,不太可行!(答案不唯一)
(2)哪些情形容易研究?从中你能发现什么规律?
长方形内有1个点、2个点、3个点、4个点等较简单的情形易研究.发现了长方形内点的个数每增加1,三角形的个数就增加2.
(3)你发现的规律正确吗?你能给出合理的解释吗?
正确.理由:每增加一个点且保证所有连线不再相交产生新的点,相当于在其中一个三角形内增加一个点,并与该三角形的三个顶点相连,分得3个三角形,此时比上一情形增加了2个三角形.
合作探究
实施计划
写出你的解决方案,并说明其中的道理.
小明是这样思考的:
(1)先研究长方形内有3个点、4个点的情形(如图).
(2)几种简单情形的数据如下表,发现规律:长方形内点的个数增加1,三角形的个数增加2.
合作探究
(3)猜想是合理的.在长方形内已经有n个点的情况下,新增的一个点要么在某个三角形内部,要么在某条线段上.当新增的这个点在某个三角形内部时,连接该点和三角形的顶点,原来的1个三角形分成3个小三角形,三角形的个数增加2;当新增的这个点在某条线段上时,连接该点和它所在两个三角形的顶点,三角形的个数同样增加2.
因此,当长方形内有35个点时,分得的三角形的个数是4+2×34=72.
合作探究
回顾反思
(1)当长方形内有100个点呢?一般地,如果长方形内有n个点呢?
当长方形内有1个点,所有连线不再产生新的点时,分得4个三角形,如果长方形内有100个点,那么分得的三角形的个数为4+(100-1)×2=202.当长方形内有n个点,所有连线不再产生新的点时,分得的三角形的个数为4+2(n-1),即2n+2.
(2)你还能提出并解决什么问题?
答案不唯一,例如:如果长方形内有50个点,所有连线不再产生新的点,那么分得的三角形的个数是多少?
(3)从简单的情形开始思考有什么好处?通过简单情形归纳一般性结论,你有哪些经验?
易寻找相应规律.经验:答案不唯一,如先发现规律,然后用符号语言表达出来.
归纳小结
1.归纳:即从几种特殊情形出发,进而找到一般规律的过程.
2.运用归纳策略寻找规律
在运用归纳策略寻找规律时,要先在若干简单情形中寻找相应的规律.初步发现规律后,可以通过更多的情形验证,再考虑 一般情况.最后,试着给出合理的解释,并用数学语言简洁地表达规律.
当堂达标
叁
当堂达标
1.观察下列多项式:a+b,a2+b3,a3+b5,a4+b7, ,则第n个多项式为( )
A.an﹣b2n﹣1B.an﹣b2 n C.an+b2n﹣1 D.an+b2 n
C
A
2.数据,□,,,,,…是按照一定规律有序排列的,则“□”里应填的数是( )
A. B. C.
当堂达标
3. 将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A.98 B.100 C.102 D.10
解析:由三角形的数阵知,第n行有n个偶数,
则得出前9行有1+2+3+4+5+6+7+8+9=45个偶数,
∴第9行最后一个数为90,
∴第10行第5个数是90+2×5=100.
B
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
1.归纳
即从几种特殊情形出发,进而找到一般规律的过程.
2.运用归纳策略寻找规律
在运用归纳策略寻找规律时,要先在若干简单情形中寻找相应的规律.初步发现规律后,可以通过更多的情形验证,再考虑一般情况.最后,试着给出合理的解释,并用数学语言简洁地表达规律.
作业布置
详见教材习题
P135-136 T1-5
谢
谢
第三章 整式及其加减
六年级上册
问题解决策略:归纳
1. 如图是由同样大小的圆按一定规律排列所组成的,其中第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆,…,按此规律排列下去,第9个图形中圆的个数是( )
A.88 B.90 C.92 D.94
课前小测
19
2. 元元在日历上圈出如图所示的呈“十”字的五个数,按照这种圈法,如果圈出的5个数的和为60,那么其中最大的数为 .
C
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
用大小相等的小正方形按一定规律拼成如图所示的图形,则第n个图形中小正方形的个数是多少?你是怎样思考的?与同伴进行交流.
解析:方法1:把各图形补成一个大正方形,会发现第n个图形中小正方形的个数是(n+1)2-1;
方法2:每个图形中从左下角的点为顶点的最大正方形中含小正方形1=12,4=22,9=32,…n2个,剩余的为2×1,2×2,2×3,…2n个,故第n个图形中小正方形的个数是n2+2n(个);
方法3:第1图形有小正方形的个数是:3=1×3;第2图形有小正方形的个数是:8=2×4;第3图形有小正方形的个数是:15=3×5;
……
可得第n个图形中小正方形的个数是n(n+2),即n2+2n(个).
新知初探
贰
合作探究
探究活动 用归纳的策略解决问题
问题 “低多边形风格”是一种数字艺术设计风格.它将整个区域分割为若干三角形,通过把相邻三角形涂上不同颜色,产生立体及光影的效果.随着三角形数量增加,效果更为斑斓绚丽(如图).
合作探究
将长方形区域分割成三角形的过程:在长方形内取一定数量的点,连同长方形的4个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到长方形内所有区域都变成三角形.
如图,当长方形内有1个点时,可分得4个三角形;当长方形内有2个点时,可分得6个三角形(不计被分割的三角形).
当长方形内有35个点时,可分得多少个三角形?
合作探究
理解问题
(1)先动手画一画,感受分割得到三角形的过程.
答案不唯一,如图.
(2)已知条件是什么?目标是什么?
已知条件是在一个长方形内有一定数量的点,以及长方形的顶点,逐步连接这些点(保持所连线不再相交产生新的点)能分得一定数量的三角形.
目标是求当长方形内有35个点时,可分得三角形的个数.
合作探究
拟定计划
(1)直接研究“长方形内有35个点”的情形,你遇到了什么困难?
画出“长方形内有35个点”分三角形的情形比较繁琐、复杂,不太可行!(答案不唯一)
(2)哪些情形容易研究?从中你能发现什么规律?
长方形内有1个点、2个点、3个点、4个点等较简单的情形易研究.发现了长方形内点的个数每增加1,三角形的个数就增加2.
(3)你发现的规律正确吗?你能给出合理的解释吗?
正确.理由:每增加一个点且保证所有连线不再相交产生新的点,相当于在其中一个三角形内增加一个点,并与该三角形的三个顶点相连,分得3个三角形,此时比上一情形增加了2个三角形.
合作探究
实施计划
写出你的解决方案,并说明其中的道理.
小明是这样思考的:
(1)先研究长方形内有3个点、4个点的情形(如图).
(2)几种简单情形的数据如下表,发现规律:长方形内点的个数增加1,三角形的个数增加2.
合作探究
(3)猜想是合理的.在长方形内已经有n个点的情况下,新增的一个点要么在某个三角形内部,要么在某条线段上.当新增的这个点在某个三角形内部时,连接该点和三角形的顶点,原来的1个三角形分成3个小三角形,三角形的个数增加2;当新增的这个点在某条线段上时,连接该点和它所在两个三角形的顶点,三角形的个数同样增加2.
因此,当长方形内有35个点时,分得的三角形的个数是4+2×34=72.
合作探究
回顾反思
(1)当长方形内有100个点呢?一般地,如果长方形内有n个点呢?
当长方形内有1个点,所有连线不再产生新的点时,分得4个三角形,如果长方形内有100个点,那么分得的三角形的个数为4+(100-1)×2=202.当长方形内有n个点,所有连线不再产生新的点时,分得的三角形的个数为4+2(n-1),即2n+2.
(2)你还能提出并解决什么问题?
答案不唯一,例如:如果长方形内有50个点,所有连线不再产生新的点,那么分得的三角形的个数是多少?
(3)从简单的情形开始思考有什么好处?通过简单情形归纳一般性结论,你有哪些经验?
易寻找相应规律.经验:答案不唯一,如先发现规律,然后用符号语言表达出来.
归纳小结
1.归纳:即从几种特殊情形出发,进而找到一般规律的过程.
2.运用归纳策略寻找规律
在运用归纳策略寻找规律时,要先在若干简单情形中寻找相应的规律.初步发现规律后,可以通过更多的情形验证,再考虑 一般情况.最后,试着给出合理的解释,并用数学语言简洁地表达规律.
当堂达标
叁
当堂达标
1.观察下列多项式:a+b,a2+b3,a3+b5,a4+b7, ,则第n个多项式为( )
A.an﹣b2n﹣1B.an﹣b2 n C.an+b2n﹣1 D.an+b2 n
C
A
2.数据,□,,,,,…是按照一定规律有序排列的,则“□”里应填的数是( )
A. B. C.
当堂达标
3. 将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A.98 B.100 C.102 D.10
解析:由三角形的数阵知,第n行有n个偶数,
则得出前9行有1+2+3+4+5+6+7+8+9=45个偶数,
∴第9行最后一个数为90,
∴第10行第5个数是90+2×5=100.
B
课堂小结
肆
课堂小结
通过本节课的学习,你有哪些收获与困惑?
1.归纳
即从几种特殊情形出发,进而找到一般规律的过程.
2.运用归纳策略寻找规律
在运用归纳策略寻找规律时,要先在若干简单情形中寻找相应的规律.初步发现规律后,可以通过更多的情形验证,再考虑一般情况.最后,试着给出合理的解释,并用数学语言简洁地表达规律.
作业布置
详见教材习题
P135-136 T1-5
谢
谢
同课章节目录
