21.6 综合与实践 获取最大利润 课件(共25张PPT) 2025-2026学年数学沪科版九年级上册
文档属性
| 名称 | 21.6 综合与实践 获取最大利润 课件(共25张PPT) 2025-2026学年数学沪科版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 510.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:24:59 | ||
图片预览






文档简介
(共25张PPT)
沪科版九年级上册 第二十一章
课程讲授
课程导入
习题解析
课堂总结
21.6 综合与实践 获取最大利润
前 言
1. 对销售中最大利润问题的理解并建立二次函数模型;(重点)
2. 从实际问题中抽象出二次函数模型.(难点)
学习目标及重难点
课程导入
顶点式、对称轴和顶点坐标公式:
回顾:二次函数
直线
课程导入
一个制造商制造一种产品,它的成本可以分为固定成本和可变成本两个部分,其中固定成本包括设计产品、建造厂房、购置设备、培训工人等费用,如果没有更换产品,我们将它看为常数;可变成本与该产品生产的件数有关,而每件产品的成本包括劳动力、材料、包装、运输等费用.例如,生产某种收音机的成本(单位:元)可以近似的表述为
其中C表示生产 t台收音机的总成本,当t=0时,
C=120t+1000 ①
C成本=120×0+1000=1000
1000元是固定成本,由此可知①式中120t表示可变成本.
制造商出售产品得到的年总收入等于出售产品的年销售量 t 和产品的销售单价 x 的乘积,设R表示年总收入,则
R年总收入=t ·x ②
制造商的年利润是出售产品的年总收入和生产这些产品的总成本之间的差额,设为 P 表示年利润,则
P利润=R年总收入-C成本
∴ P利润=R-C=t·x-c ③
课程导入
问题①
当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路,一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降.假设某市场分析专家提供了下列数据:
设生产t件该产品的成本为 C=50t+1000
课程讲授
新课推进
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
课程讲授
新课推进
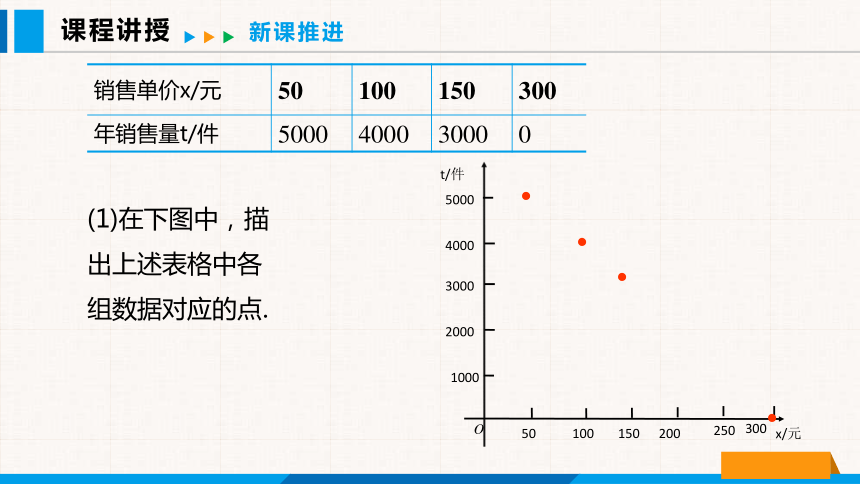
(1)在下图中,描出上述表格中各组数据对应的点.
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
O
·
·
·
·
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
课程讲授
新课推进
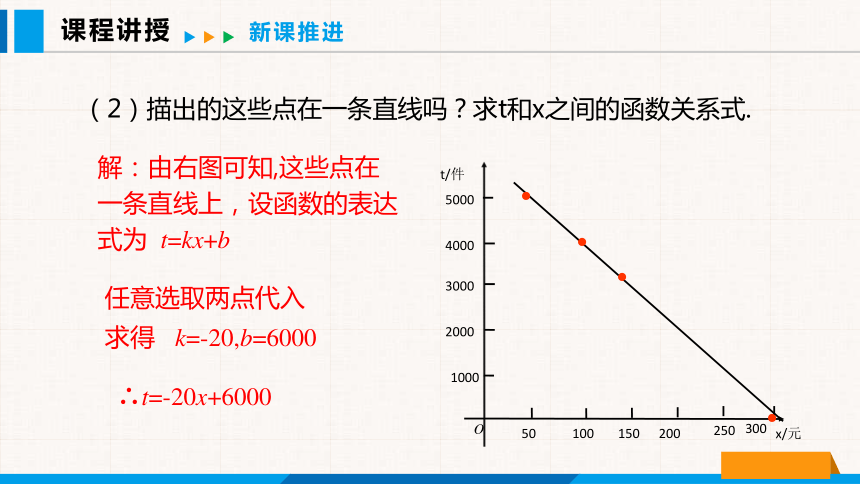
(2)描出的这些点在一条直线吗?求t和x之间的函数关系式.
解:由右图可知,这些点在一条直线上,设函数的表达式为 t=kx+b
任意选取两点代入
求得 k=-20,b=6000
∴t=-20x+6000
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
O
·
·
·
·
课程讲授
新课推进
(3)销售单价x和年销售量t各为多少时,年利润P最大?
=(-20x+6000)x-50(-20x+6000)-1000
解:∵R年总收入=t ·x
∴R年总收入=(-20x+6000) ·x
∴P利润=R年总收入-C成本=t·x-c
∴P利润=t ·x -(50t+1000)
=-20x +7000x-301000
由公式可得, 当 x= 时, 即x=175,∴t=-20x+6000=2500,
P最大 = =311500元.
课程讲授
新课推进
制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据;
问题②
设生产t件某种电子产品的成本(单位:元)可以近似的表示为
C=1000t+2 000 000
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
课程讲授
新课推进
(1)在图中,描出上述表格中各组数据对应的点;
3500
2000
2500
3000
4000
1000
2000
3000
4000
7000
8000
t/件
x/元
0
5000
6000
9000
10000
·
·
·
·
·
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
课程讲授
新课推进
(2)请你帮助制造商分析,当年销售量t和销售单价 x 分别是多少时,年利润 P 最大?并说说你有几种求解方法?与同学进行交流.
课程讲授
新课推进
解:通过图象可以观察,这些点几乎在一条直线上,不妨设表达式为 x=kt+b
将点(3000,3400)和点(8500,2300)代入x=kt+b中可得
∵R年总收入= x·t
∴P利润=R年总收入-C成本=x·t-c
课程讲授
新课推进
∴ x=2500
当 t= 时,即t =7500时,年利润P最大.
记当年销量是7500件,销售单价x是2500元时,年利润P最大.
某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元. (1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得,当40≤x≤50时, Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
课程讲授
新课推进
问题③
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵ 线段过(50,60)和(70,20).
∴
∴ y =-2x +160(50≤x≤70)
解得
课程讲授
新课推进
∴y =-2x +160(50≤x≤70)
∴Q=(x-30)y
=(x-30)(-2x + 160)
=-2x2 + 220x- 4800
=-2(x-55)2 +1250 (50≤x≤70)
∵a = -2<0,图象开口向下,
∴当x = 55时,Q最大= 1250
∴当售价在50~70元时,售价x是55元时,获利最大,
最大利润是1250元.
课程讲授
新课推进
解:∵ 当40≤x≤50时, Q最大= 1200<1218
当50≤x≤70时, Q最大= 1250>1218 . ∴ 售价x应在50~70元之间.
∴令-2(x-55)2 +1250=1218, 解得 x1=51,x2=59
当x1=51时,y1=-2x+160=-2×51+160= 58(件)
当x2=59时,y2=-2x+160= -2×59+160= 42(件)
∴ 若4月份该商品销售后的总利润为1218元,则该商品售价为51元或59元,当月的销售量分别为58件或42件.
(3)若4月份该商品销售后的总利润为1218元,则该商品售价与当月的销售量各是多少?
课程讲授
新课推进
进价为80元的某衬衣定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
习题解析
习题1
若日销售量 y 是销售价 x 的一次函数.
(1)求出日销售量 y(件)与销售价 x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下:
习题解析
习题2
x(元) 15 20 30 …
y(件) 25 20 10 …
习题解析
(2)设每件产品的销售价应定为 x 元,所获销售利润为 w 元.则
产品的销售价应定为25元,此时每日获得最大销售利润为225元.
则
解得 k =-1,b=40,
解:(1)设此一次函数表达式为 .
所以一次函数表达为 .
习题3
习题解析
一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) … 50 60 70 80 …
销售量y(千克) … 100 90 80 70 …
习题解析
(1)求y与x的函数表达式;
(2)该批发商若想获得4 000元的利润,应将售价定为多少?
(3)该产品每千克售价为多少元时,批发商获得的利润W(元)最大?此时的最大利润为多少元?
解:(1)设y与x的函数表达式为y=kx+b(k≠0),
根据题意得 ,解得
故y与x的函数表达式为y=-x+150;
习题解析
(2)根据题意得(-x+150)(x-20)=4 000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4 000元的利润,应将售价定为70元;
(3)W与x的函数表达式为
W=(-x+150)(x-20)=-x2+170x-3 000=-(x-85)2+4 225,
∵-1<0,∴当x=85时,W值最大,W最大值是4 225.
∴该产品每千克售价为85元时,批发商获得的利润W(元)最大,此时的最大利润为4 225元.
小结
课堂总结
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价: 要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
求最大值利用配方法或公式也可利用函数简图和性质求出.
最大利润问题
沪科版九年级上册 第二十一章
课程讲授
课程导入
习题解析
课堂总结
21.6 综合与实践 获取最大利润
前 言
1. 对销售中最大利润问题的理解并建立二次函数模型;(重点)
2. 从实际问题中抽象出二次函数模型.(难点)
学习目标及重难点
课程导入
顶点式、对称轴和顶点坐标公式:
回顾:二次函数
直线
课程导入
一个制造商制造一种产品,它的成本可以分为固定成本和可变成本两个部分,其中固定成本包括设计产品、建造厂房、购置设备、培训工人等费用,如果没有更换产品,我们将它看为常数;可变成本与该产品生产的件数有关,而每件产品的成本包括劳动力、材料、包装、运输等费用.例如,生产某种收音机的成本(单位:元)可以近似的表述为
其中C表示生产 t台收音机的总成本,当t=0时,
C=120t+1000 ①
C成本=120×0+1000=1000
1000元是固定成本,由此可知①式中120t表示可变成本.
制造商出售产品得到的年总收入等于出售产品的年销售量 t 和产品的销售单价 x 的乘积,设R表示年总收入,则
R年总收入=t ·x ②
制造商的年利润是出售产品的年总收入和生产这些产品的总成本之间的差额,设为 P 表示年利润,则
P利润=R年总收入-C成本
∴ P利润=R-C=t·x-c ③
课程导入
问题①
当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路,一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降.假设某市场分析专家提供了下列数据:
设生产t件该产品的成本为 C=50t+1000
课程讲授
新课推进
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
课程讲授
新课推进
(1)在下图中,描出上述表格中各组数据对应的点.
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
O
·
·
·
·
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
课程讲授
新课推进
(2)描出的这些点在一条直线吗?求t和x之间的函数关系式.
解:由右图可知,这些点在一条直线上,设函数的表达式为 t=kx+b
任意选取两点代入
求得 k=-20,b=6000
∴t=-20x+6000
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
O
·
·
·
·
课程讲授
新课推进
(3)销售单价x和年销售量t各为多少时,年利润P最大?
=(-20x+6000)x-50(-20x+6000)-1000
解:∵R年总收入=t ·x
∴R年总收入=(-20x+6000) ·x
∴P利润=R年总收入-C成本=t·x-c
∴P利润=t ·x -(50t+1000)
=-20x +7000x-301000
由公式可得, 当 x= 时, 即x=175,∴t=-20x+6000=2500,
P最大 = =311500元.
课程讲授
新课推进
制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据;
问题②
设生产t件某种电子产品的成本(单位:元)可以近似的表示为
C=1000t+2 000 000
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
课程讲授
新课推进
(1)在图中,描出上述表格中各组数据对应的点;
3500
2000
2500
3000
4000
1000
2000
3000
4000
7000
8000
t/件
x/元
0
5000
6000
9000
10000
·
·
·
·
·
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
课程讲授
新课推进
(2)请你帮助制造商分析,当年销售量t和销售单价 x 分别是多少时,年利润 P 最大?并说说你有几种求解方法?与同学进行交流.
课程讲授
新课推进
解:通过图象可以观察,这些点几乎在一条直线上,不妨设表达式为 x=kt+b
将点(3000,3400)和点(8500,2300)代入x=kt+b中可得
∵R年总收入= x·t
∴P利润=R年总收入-C成本=x·t-c
课程讲授
新课推进
∴ x=2500
当 t= 时,即t =7500时,年利润P最大.
记当年销量是7500件,销售单价x是2500元时,年利润P最大.
某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元. (1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得,当40≤x≤50时, Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
课程讲授
新课推进
问题③
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵ 线段过(50,60)和(70,20).
∴
∴ y =-2x +160(50≤x≤70)
解得
课程讲授
新课推进
∴y =-2x +160(50≤x≤70)
∴Q=(x-30)y
=(x-30)(-2x + 160)
=-2x2 + 220x- 4800
=-2(x-55)2 +1250 (50≤x≤70)
∵a = -2<0,图象开口向下,
∴当x = 55时,Q最大= 1250
∴当售价在50~70元时,售价x是55元时,获利最大,
最大利润是1250元.
课程讲授
新课推进
解:∵ 当40≤x≤50时, Q最大= 1200<1218
当50≤x≤70时, Q最大= 1250>1218 . ∴ 售价x应在50~70元之间.
∴令-2(x-55)2 +1250=1218, 解得 x1=51,x2=59
当x1=51时,y1=-2x+160=-2×51+160= 58(件)
当x2=59时,y2=-2x+160= -2×59+160= 42(件)
∴ 若4月份该商品销售后的总利润为1218元,则该商品售价为51元或59元,当月的销售量分别为58件或42件.
(3)若4月份该商品销售后的总利润为1218元,则该商品售价与当月的销售量各是多少?
课程讲授
新课推进
进价为80元的某衬衣定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
习题解析
习题1
若日销售量 y 是销售价 x 的一次函数.
(1)求出日销售量 y(件)与销售价 x(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下:
习题解析
习题2
x(元) 15 20 30 …
y(件) 25 20 10 …
习题解析
(2)设每件产品的销售价应定为 x 元,所获销售利润为 w 元.则
产品的销售价应定为25元,此时每日获得最大销售利润为225元.
则
解得 k =-1,b=40,
解:(1)设此一次函数表达式为 .
所以一次函数表达为 .
习题3
习题解析
一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的销售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) … 50 60 70 80 …
销售量y(千克) … 100 90 80 70 …
习题解析
(1)求y与x的函数表达式;
(2)该批发商若想获得4 000元的利润,应将售价定为多少?
(3)该产品每千克售价为多少元时,批发商获得的利润W(元)最大?此时的最大利润为多少元?
解:(1)设y与x的函数表达式为y=kx+b(k≠0),
根据题意得 ,解得
故y与x的函数表达式为y=-x+150;
习题解析
(2)根据题意得(-x+150)(x-20)=4 000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4 000元的利润,应将售价定为70元;
(3)W与x的函数表达式为
W=(-x+150)(x-20)=-x2+170x-3 000=-(x-85)2+4 225,
∵-1<0,∴当x=85时,W值最大,W最大值是4 225.
∴该产品每千克售价为85元时,批发商获得的利润W(元)最大,此时的最大利润为4 225元.
小结
课堂总结
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价: 要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
求最大值利用配方法或公式也可利用函数简图和性质求出.
最大利润问题
