22.1 第4课时 平行线分线段成比例定理及推论 课件(共25张PPT) 2025-2026学年数学沪科版(2024)九年级上册
文档属性
| 名称 | 22.1 第4课时 平行线分线段成比例定理及推论 课件(共25张PPT) 2025-2026学年数学沪科版(2024)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 422.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 21:51:03 | ||
图片预览





文档简介
(共25张PPT)
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.1 比例线段
第四课时 平行线分线段成比例定理及推论
前 言
1. 平行线分线段成比例定理和推论及其应用;(重点)
2. 会用平行线分线段成比例及其推论解决相关问题.(难点)
学习目标及重难点
课程导入
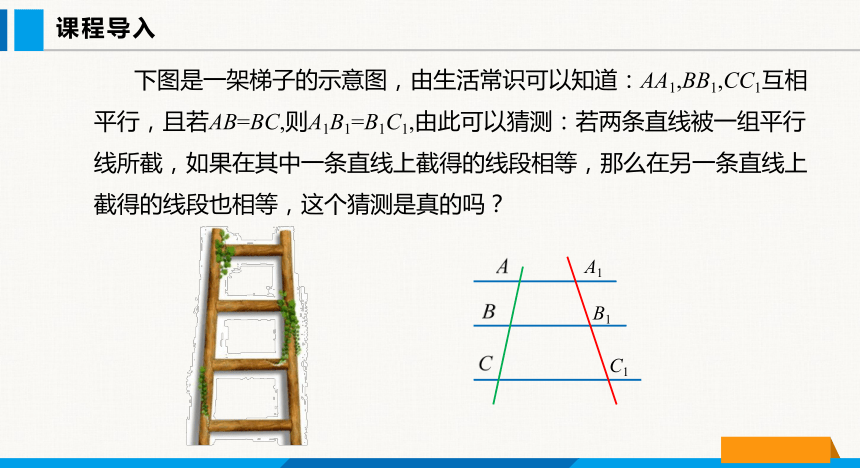
下图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1互相平行,且若AB=BC,则A1B1=B1C1,由此可以猜测:若两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等,这个猜测是真的吗?
A1
C1
B1
已知,直线 l1、l2、l3 互相平行,直线AC和直线A1C1分别交直线 l1、l2、l3 于点 A、B、C 和点 A1、B1、C1,且 AB=BC .求证:A1B1=B1C1.
l1
l2
l3
A
B
C
A1
B1
C1
E
F
证明:
过点B1作EF∥ AC,
分别交直线 l1、l3 于点 E、F.
∴ 四边形ABB1E和四边形BCFB1都是平行四边形
∵ AB=BC
∴ EB1=B1F
∵ l1∥ l3
∴∠A1EB1=∠C1FB1
∴ AB=EB1,
BC=B1F
在△A1B1E和△C1B1F中
∵
∠A1B1E=∠C1B1F
EB1=FB1
∠A1EB1=∠B1FC1
∴ △A1B1E≌△C1B1F
∴ A1B1=B1C1
(ASA)
课程导入
课程导入
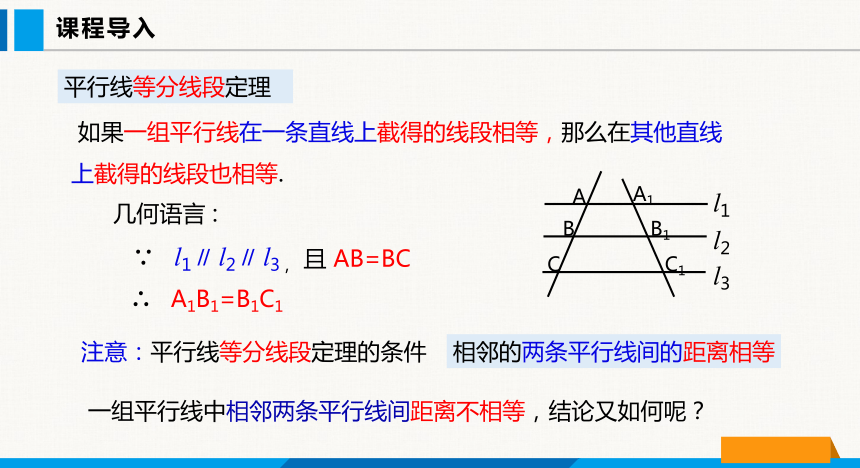
由此得到如下结论:
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
平行线等分线段定理
l1
l2
l3
A
B
C
A1
B1
C1
几何语言 :
∵ l1∥ l2∥ l3 ,
∴ A1B1=B1C1
且 AB=BC
注意:平行线等分线段定理的条件
相邻的两条平行线间的距离相等
一组平行线中相邻两条平行线间距离不相等,结论又如何呢?
课程导入
如图,有一组平行线:l1∥ l2∥ l3 ··· lk∥ ··· ln-1∥ ln,另外,直线 A1An与直线 B1Bn 被这一组平行直线分别截于点 A1,A2,A3,···,Ak,···,An-1,An 和点 B1,B2,B3,···,Bk,···,Bn-1,Bn .根据已学定理,可以得到:如果 A1A2=A2A3=···=An-1An,那么 B1B2=B2B3=···=Bn-1Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
Bk
Bn-1
Bn
l1
l2
l3
lk
ln
ln-1
思考:
A1Ak
AkAn
与 相等吗?
B1Bk
BkBn
这时,如设
A1A2=A2A3=···=An-1An=a,
B1B2=B2B3=···=Bn-1Bn=b,
容易推得:
A1Ak
AkAn
=
(k-1)a
(n-k)a
=
k-1
n-k
B1Bk
BkBn
=
(k-1)b
(n-k)b
=
k-1
n-k
∴
A1Ak
AkAn
B1Bk
BkBn
=
,
A1Ak
A1An
B1Bk
B1Bn
AkAn
A1An
BkBn
B1Bn
,
,
A1Ak
A1An
B1Bk
B1Bn
=
AkAn
A1An
BkBn
B1Bn
=
是指同一条直线上的两条线段的比,
3、对应线段的比相等
两条直线被
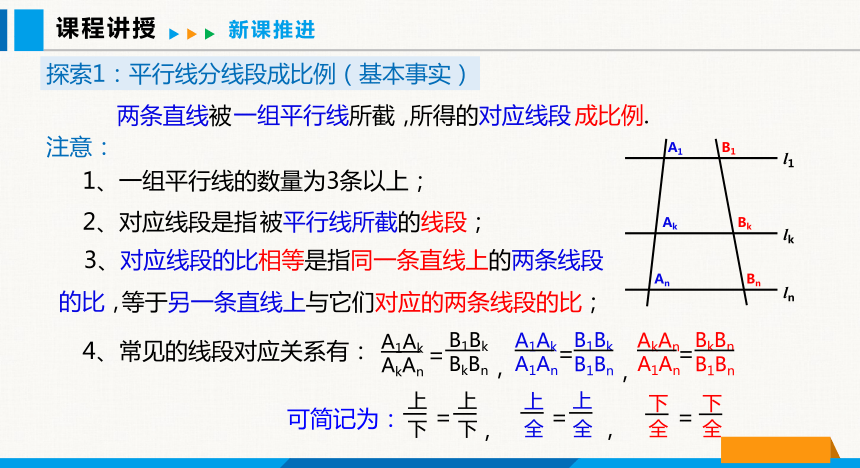
探索1:平行线分线段成比例(基本事实)
注意:
1、一组平行线的数量为3条以上;
4、常见的线段对应关系有:
2、对应线段是指
A1
Ak
An
B1
Bk
Bn
l1
lk
ln
A1Ak
AkAn
B1Bk
BkBn
=
A1Ak
A1An
B1Bk
B1Bn
AkAn
A1An
BkBn
B1Bn
,
,
=
=
可简记为:
上
下
=
上
全
下
全
,
,
=
=
上
下
上
全
下
全
所得的对应线段
一组平行线所截,
成比例.
被平行线所截的线段;
等于另一条直线上与它们对应的两条线段的比;
课程讲授
新课推进
课程讲授
新课推进
平行线分线段成比例定理
A
B
C
D
E
F
l1
l2
l3
几何语言 :
∵ l1∥ l2∥ l3
AB
AC
DE
DF
BC
AC
EF
DF
∴
AB
BC
DE
EF
=
,
,
=
=
可简记为:
上
下
=
上
全
下
全
,
,
=
=
上
下
上
全
下
全
两条直线被
所得的对应线段
一组平行线所截,
成比例.
课程讲授
新课推进
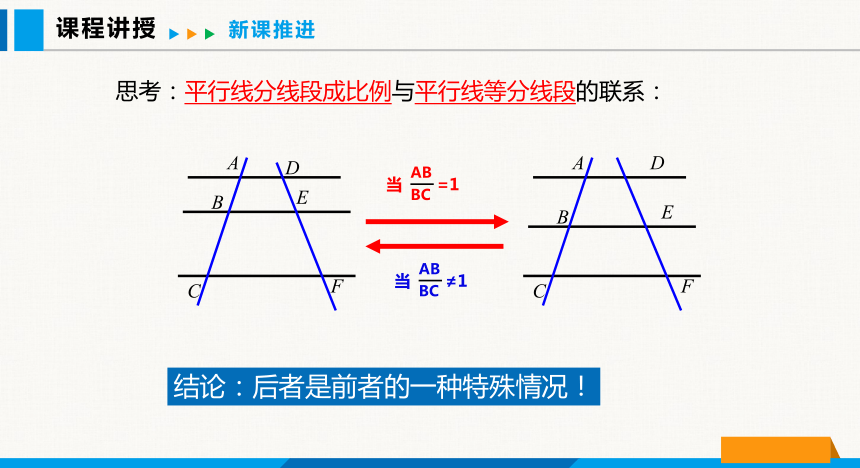
思考:平行线分线段成比例与平行线等分线段的联系:
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
AB
BC
当 =1
AB
BC
当 ≠1
如图,直线a∥b∥ c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段.
A1
A2
A3
B1
B2
B3
b
c
m
n
a
把直线 n 向左或向右任意平移,这些线段依然成比例.
课程讲授
新课推进
探索2:平行线分线段成比例定理的推论
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B1 与A1 重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
课程讲授
新课推进
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B2 与A2 重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
( )
课程讲授
新课推进
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳:
课程讲授
新课推进
运用平行线分线段成比例定理的三种基本图形:
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
(1) 两条截线无交点
(2) 两条截线的交点在三条平行线的外面
(3)两条截线的交点在三条平行线的内部
课程讲授
新课推进
C
B
如图,直线DE平行于△ABC的一边BC,并分别交另两边AB,AC与点D,E. 则
A
E
D
M
N
AD
DB
=
AE
EC
,
AD
AB
=
AE
AC
和
BD
AB
=
EC
AC
成立吗?
为什么?
过点A作直线MN∥ DE
∵ DE∥ BC
又∵ AB,AC被一组平行线MN,DE,BC所截
∴ MN∥ DE∥ BC
解:
AD
DB
=
AE
EC
,
AD
AB
=
AE
AC
和
DB
AB
=
EC
AC
∴
( 平行线分线段成比例定理 )
由此得到以下结论:
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
课程讲授
新课推进
如图,直线DE平行于△ABC的一边BC,并分别交另两边AB,AC的延长线于点D,E. 对应线段还成比例吗?
由此可以得到以下结论:
C
B
A
D
E
M
N
C
B
A
N
M
E
D
(1) DE在三角形的顺向延长线上;
(2) DE在三角形的反向延长线上;
平行于三角形一边的直线截其他两边的延长线,所得的对应线段成比例.
思考:
AB
BD
=
AC
CE
,
AB
AD
=
AC
AE
和
BD
AD
=
CE
AE
AD
AB
=
AE
AC
,
AD
BD
=
AE
EC
和
AB
BD
=
AC
EC
课程讲授
新课推进
C
B
A
D
E
C
B
A
E
D
① 截线在三角形的内部;
② 截线在三角形的顺向延长线上;
③ 截线在三角形的反向延长线上.
C
B
A
E
D
几何语言 :
AD
AB
=
AE
AC
和
DB
AB
=
EC
AC
AD
DB
=
AE
EC
,
∴
②
∵ DE∥ BC
①
∵ DE∥ BC
∴
AB
BD
=
AC
CE
,
AB
AD
=
AC
AE
和
BD
AD
=
CE
AE
③
∵ DE∥ BC
∴
AD
AB
=
AE
AC
,
AD
BD
=
AE
EC
和
AB
BD
=
AC
EC
A 字形图
X 字形图
小结
课程讲授
推论:平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
习题1
如图,已知AB∥ CD∥ EF,AF交BE于点H,下列结论中错误的是( )
A.
B.
C.
D.
在题目中如遇到与直线平行相关的问题时,可从两个方面获取信息:
一是位置角之间的关系( 同位角相等、内错角相等、同旁内角互补 );
二是线段之间的关系,即平行线分线段成比例.
习题解析
C
习题解析
习题2
如图,直线 l1∥ l2∥ l3,直线AC分别交这三条直线于点A,B,C,直线DF分别交这三条直线于点D,E,F,若 AB=3,DE= ,EF=4,求BC的长.
7
2
A
B
C
D
E
l1
l2
l3
F
3
7
2
4
?
规律总结:
∵ 直线 l1∥ l2∥ l3,
解:
AB
BC
=
DE
EF
∴
又∵ AB=3,DE= ,EF=4
7
2
3
BC
=
4
∴
7
2
解得
BC=
24
7
利用平行线分线段成比例的定理及推论求线段长时,先确定图中的平行线,由此联想到平行线截得的线段间的比例关系,结合待求线段和已知线段写出一个含有它们的比例式,构造方程,解方程求出待求线段长.
习题解析
习题3
如图,已知直线 a∥ b∥ c,直线 m,n 与直线 a,b,c 分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,求BF的长.
A
B
C
a
b
4
D
F
c
m
n
6
3
E
又∵ AC=4,CE=6,BD=3
∵ a∥ b∥ c
解:
AC
CE
=
BD
DF
∴
∴
4
6
=
3
DF
解得
DF=
9
2
∴ BF=
BD+DF
=3+
9
2
=
15
2
习题4
习题解析
已知:EG∥ BC,GF∥ CD
求证:
D
F
A
B
C
E
G
AE
AB
=
AF
AD
∵ EG∥ BC
解:
∴
AE
AB
=
AG
AC
∵ GF∥ CD
∴
AG
AC
=
AF
AD
∴
AE
AB
=
AF
AD
注意:
若不能直接证明两组比相等,则可以证明这两组比分别与另一组比相等,从而通过等量代换证明这两组比相等.
习题5
习题解析
【中考·临沂】如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥ BC,EF∥ AB.若AB=8,BD=3,BF=4,求 FC 的长.
利用平行线分线段成比例的定理及推论求线段长时,先根据已知的平行线写出比例式,利用中间比进行等量代换,建立起已知线段和未知线段的桥梁.
∵ DE∥ BC
解:
∴
AD
BD
=
AE
EC
∵ EF∥ AB
∴
AE
EC
=
BF
FC
∴
AD
BD
=
BF
FC
∵ AB=8,BD=3,BF=4
∴
5
3
=
4
FC
解得
FC=
12
5
∴ AD=AB-BD=5
规律总结:
习题6
习题解析
如图,E 为 ABCD的边CD的延长线上的一点,连接BE,交AC于点O,交AD于点F. 求证:BO2=OF·OE.
∵ 四边形ABCD是平行四边形
解:
∴ AD∥ BC,AB∥ CD
∴ ,
OF
BO
=
OA
OC
OA
OC
BO
OE
=
∴
OF
BO
=
BO
OE
∴ BO2=OF·OE
课程总结
小结
平行线分线段成比例定理
两条直线被一组平行线所截,所得的对应线段成比例.
A
B
C
D
E
F
l1
l2
l3
注意:
1、一组平行线的数量为3条以上;
2、对应线段是指被平行线所截的线段;
3、对应线段的比相等是指同一条直线上的两条线段的比,等于另一条直线上与它们对应的两条线段的比;
几何语言 :
∵ l1∥ l2∥ l3
BC
AC
EF
DF
=
可简记为:
上
下
=
上
全
下
全
,
,
=
=
上
下
上
全
下
全
AB
AC
DE
DF
,
=
∴
AB
BC
DE
EF
=
,
课程总结
小结
基本事实
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
平行线分线段成比例
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.1 比例线段
第四课时 平行线分线段成比例定理及推论
前 言
1. 平行线分线段成比例定理和推论及其应用;(重点)
2. 会用平行线分线段成比例及其推论解决相关问题.(难点)
学习目标及重难点
课程导入
下图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1互相平行,且若AB=BC,则A1B1=B1C1,由此可以猜测:若两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等,这个猜测是真的吗?
A1
C1
B1
已知,直线 l1、l2、l3 互相平行,直线AC和直线A1C1分别交直线 l1、l2、l3 于点 A、B、C 和点 A1、B1、C1,且 AB=BC .求证:A1B1=B1C1.
l1
l2
l3
A
B
C
A1
B1
C1
E
F
证明:
过点B1作EF∥ AC,
分别交直线 l1、l3 于点 E、F.
∴ 四边形ABB1E和四边形BCFB1都是平行四边形
∵ AB=BC
∴ EB1=B1F
∵ l1∥ l3
∴∠A1EB1=∠C1FB1
∴ AB=EB1,
BC=B1F
在△A1B1E和△C1B1F中
∵
∠A1B1E=∠C1B1F
EB1=FB1
∠A1EB1=∠B1FC1
∴ △A1B1E≌△C1B1F
∴ A1B1=B1C1
(ASA)
课程导入
课程导入
由此得到如下结论:
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.
平行线等分线段定理
l1
l2
l3
A
B
C
A1
B1
C1
几何语言 :
∵ l1∥ l2∥ l3 ,
∴ A1B1=B1C1
且 AB=BC
注意:平行线等分线段定理的条件
相邻的两条平行线间的距离相等
一组平行线中相邻两条平行线间距离不相等,结论又如何呢?
课程导入
如图,有一组平行线:l1∥ l2∥ l3 ··· lk∥ ··· ln-1∥ ln,另外,直线 A1An与直线 B1Bn 被这一组平行直线分别截于点 A1,A2,A3,···,Ak,···,An-1,An 和点 B1,B2,B3,···,Bk,···,Bn-1,Bn .根据已学定理,可以得到:如果 A1A2=A2A3=···=An-1An,那么 B1B2=B2B3=···=Bn-1Bn .
A1
A2
A3
Ak
An-1
An
B1
B2
B3
Bk
Bn-1
Bn
l1
l2
l3
lk
ln
ln-1
思考:
A1Ak
AkAn
与 相等吗?
B1Bk
BkBn
这时,如设
A1A2=A2A3=···=An-1An=a,
B1B2=B2B3=···=Bn-1Bn=b,
容易推得:
A1Ak
AkAn
=
(k-1)a
(n-k)a
=
k-1
n-k
B1Bk
BkBn
=
(k-1)b
(n-k)b
=
k-1
n-k
∴
A1Ak
AkAn
B1Bk
BkBn
=
,
A1Ak
A1An
B1Bk
B1Bn
AkAn
A1An
BkBn
B1Bn
,
,
A1Ak
A1An
B1Bk
B1Bn
=
AkAn
A1An
BkBn
B1Bn
=
是指同一条直线上的两条线段的比,
3、对应线段的比相等
两条直线被
探索1:平行线分线段成比例(基本事实)
注意:
1、一组平行线的数量为3条以上;
4、常见的线段对应关系有:
2、对应线段是指
A1
Ak
An
B1
Bk
Bn
l1
lk
ln
A1Ak
AkAn
B1Bk
BkBn
=
A1Ak
A1An
B1Bk
B1Bn
AkAn
A1An
BkBn
B1Bn
,
,
=
=
可简记为:
上
下
=
上
全
下
全
,
,
=
=
上
下
上
全
下
全
所得的对应线段
一组平行线所截,
成比例.
被平行线所截的线段;
等于另一条直线上与它们对应的两条线段的比;
课程讲授
新课推进
课程讲授
新课推进
平行线分线段成比例定理
A
B
C
D
E
F
l1
l2
l3
几何语言 :
∵ l1∥ l2∥ l3
AB
AC
DE
DF
BC
AC
EF
DF
∴
AB
BC
DE
EF
=
,
,
=
=
可简记为:
上
下
=
上
全
下
全
,
,
=
=
上
下
上
全
下
全
两条直线被
所得的对应线段
一组平行线所截,
成比例.
课程讲授
新课推进
思考:平行线分线段成比例与平行线等分线段的联系:
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
AB
BC
当 =1
AB
BC
当 ≠1
如图,直线a∥b∥ c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段.
A1
A2
A3
B1
B2
B3
b
c
m
n
a
把直线 n 向左或向右任意平移,这些线段依然成比例.
课程讲授
新课推进
探索2:平行线分线段成比例定理的推论
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B1 与A1 重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
课程讲授
新课推进
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B2 与A2 重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
( )
课程讲授
新课推进
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳:
课程讲授
新课推进
运用平行线分线段成比例定理的三种基本图形:
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
(1) 两条截线无交点
(2) 两条截线的交点在三条平行线的外面
(3)两条截线的交点在三条平行线的内部
课程讲授
新课推进
C
B
如图,直线DE平行于△ABC的一边BC,并分别交另两边AB,AC与点D,E. 则
A
E
D
M
N
AD
DB
=
AE
EC
,
AD
AB
=
AE
AC
和
BD
AB
=
EC
AC
成立吗?
为什么?
过点A作直线MN∥ DE
∵ DE∥ BC
又∵ AB,AC被一组平行线MN,DE,BC所截
∴ MN∥ DE∥ BC
解:
AD
DB
=
AE
EC
,
AD
AB
=
AE
AC
和
DB
AB
=
EC
AC
∴
( 平行线分线段成比例定理 )
由此得到以下结论:
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
课程讲授
新课推进
如图,直线DE平行于△ABC的一边BC,并分别交另两边AB,AC的延长线于点D,E. 对应线段还成比例吗?
由此可以得到以下结论:
C
B
A
D
E
M
N
C
B
A
N
M
E
D
(1) DE在三角形的顺向延长线上;
(2) DE在三角形的反向延长线上;
平行于三角形一边的直线截其他两边的延长线,所得的对应线段成比例.
思考:
AB
BD
=
AC
CE
,
AB
AD
=
AC
AE
和
BD
AD
=
CE
AE
AD
AB
=
AE
AC
,
AD
BD
=
AE
EC
和
AB
BD
=
AC
EC
课程讲授
新课推进
C
B
A
D
E
C
B
A
E
D
① 截线在三角形的内部;
② 截线在三角形的顺向延长线上;
③ 截线在三角形的反向延长线上.
C
B
A
E
D
几何语言 :
AD
AB
=
AE
AC
和
DB
AB
=
EC
AC
AD
DB
=
AE
EC
,
∴
②
∵ DE∥ BC
①
∵ DE∥ BC
∴
AB
BD
=
AC
CE
,
AB
AD
=
AC
AE
和
BD
AD
=
CE
AE
③
∵ DE∥ BC
∴
AD
AB
=
AE
AC
,
AD
BD
=
AE
EC
和
AB
BD
=
AC
EC
A 字形图
X 字形图
小结
课程讲授
推论:平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
习题1
如图,已知AB∥ CD∥ EF,AF交BE于点H,下列结论中错误的是( )
A.
B.
C.
D.
在题目中如遇到与直线平行相关的问题时,可从两个方面获取信息:
一是位置角之间的关系( 同位角相等、内错角相等、同旁内角互补 );
二是线段之间的关系,即平行线分线段成比例.
习题解析
C
习题解析
习题2
如图,直线 l1∥ l2∥ l3,直线AC分别交这三条直线于点A,B,C,直线DF分别交这三条直线于点D,E,F,若 AB=3,DE= ,EF=4,求BC的长.
7
2
A
B
C
D
E
l1
l2
l3
F
3
7
2
4
?
规律总结:
∵ 直线 l1∥ l2∥ l3,
解:
AB
BC
=
DE
EF
∴
又∵ AB=3,DE= ,EF=4
7
2
3
BC
=
4
∴
7
2
解得
BC=
24
7
利用平行线分线段成比例的定理及推论求线段长时,先确定图中的平行线,由此联想到平行线截得的线段间的比例关系,结合待求线段和已知线段写出一个含有它们的比例式,构造方程,解方程求出待求线段长.
习题解析
习题3
如图,已知直线 a∥ b∥ c,直线 m,n 与直线 a,b,c 分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,求BF的长.
A
B
C
a
b
4
D
F
c
m
n
6
3
E
又∵ AC=4,CE=6,BD=3
∵ a∥ b∥ c
解:
AC
CE
=
BD
DF
∴
∴
4
6
=
3
DF
解得
DF=
9
2
∴ BF=
BD+DF
=3+
9
2
=
15
2
习题4
习题解析
已知:EG∥ BC,GF∥ CD
求证:
D
F
A
B
C
E
G
AE
AB
=
AF
AD
∵ EG∥ BC
解:
∴
AE
AB
=
AG
AC
∵ GF∥ CD
∴
AG
AC
=
AF
AD
∴
AE
AB
=
AF
AD
注意:
若不能直接证明两组比相等,则可以证明这两组比分别与另一组比相等,从而通过等量代换证明这两组比相等.
习题5
习题解析
【中考·临沂】如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥ BC,EF∥ AB.若AB=8,BD=3,BF=4,求 FC 的长.
利用平行线分线段成比例的定理及推论求线段长时,先根据已知的平行线写出比例式,利用中间比进行等量代换,建立起已知线段和未知线段的桥梁.
∵ DE∥ BC
解:
∴
AD
BD
=
AE
EC
∵ EF∥ AB
∴
AE
EC
=
BF
FC
∴
AD
BD
=
BF
FC
∵ AB=8,BD=3,BF=4
∴
5
3
=
4
FC
解得
FC=
12
5
∴ AD=AB-BD=5
规律总结:
习题6
习题解析
如图,E 为 ABCD的边CD的延长线上的一点,连接BE,交AC于点O,交AD于点F. 求证:BO2=OF·OE.
∵ 四边形ABCD是平行四边形
解:
∴ AD∥ BC,AB∥ CD
∴ ,
OF
BO
=
OA
OC
OA
OC
BO
OE
=
∴
OF
BO
=
BO
OE
∴ BO2=OF·OE
课程总结
小结
平行线分线段成比例定理
两条直线被一组平行线所截,所得的对应线段成比例.
A
B
C
D
E
F
l1
l2
l3
注意:
1、一组平行线的数量为3条以上;
2、对应线段是指被平行线所截的线段;
3、对应线段的比相等是指同一条直线上的两条线段的比,等于另一条直线上与它们对应的两条线段的比;
几何语言 :
∵ l1∥ l2∥ l3
BC
AC
EF
DF
=
可简记为:
上
下
=
上
全
下
全
,
,
=
=
上
下
上
全
下
全
AB
AC
DE
DF
,
=
∴
AB
BC
DE
EF
=
,
课程总结
小结
基本事实
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
平行线分线段成比例
