22.2 第2课时 三角形相似的判定定理1 课件(共17张PPT) 2025-2026学年数学沪科版(2024)九年级上册
文档属性
| 名称 | 22.2 第2课时 三角形相似的判定定理1 课件(共17张PPT) 2025-2026学年数学沪科版(2024)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 418.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:50:50 | ||
图片预览




文档简介
(共17张PPT)
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.2 相似三角形的判定
第二课时 三角形相似的判定定理1
前 言
1.理解相似三角形的定义,掌握定义中的两个条件;(重点)
2.掌握并熟练运用相似三角形的判定定理1.(难点)
A
B
C
C′
B′
A′
学习目标及重难点
课程导入
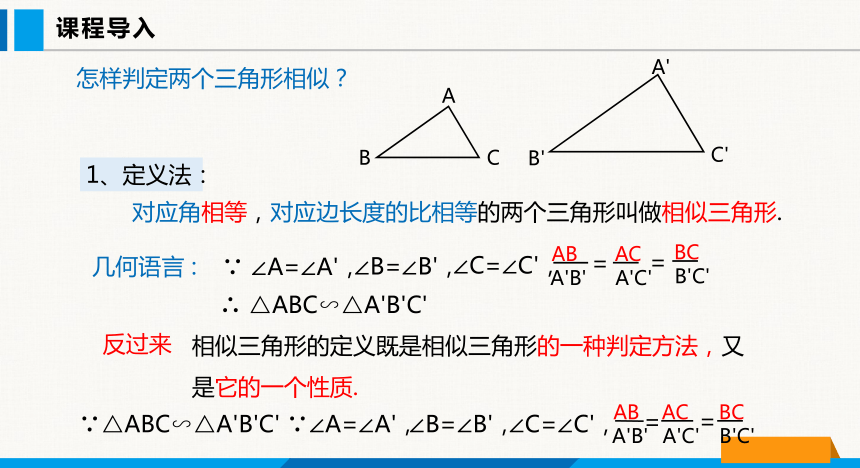
怎样判定两个三角形相似?
1、定义法:
对应角相等,对应边长度的比相等的两个三角形叫做相似三角形.
∵ ∠A=∠A',
∠B=∠B',
∠C=∠C',
AB
A'B'
=
AC
A'C'
=
BC
B'C'
几何语言 :
∴ △ABC∽△A'B'C'
反过来
∵∠A=∠A',
∠B=∠B',
∠C=∠C',
AB
A'B'
=
AC
A'C'
=
BC
B'C'
∵△ABC∽△A'B'C'
相似三角形的定义既是相似三角形的一种判定方法,又是它的一个性质.
A
B
C
A'
C'
B'
x 型相似
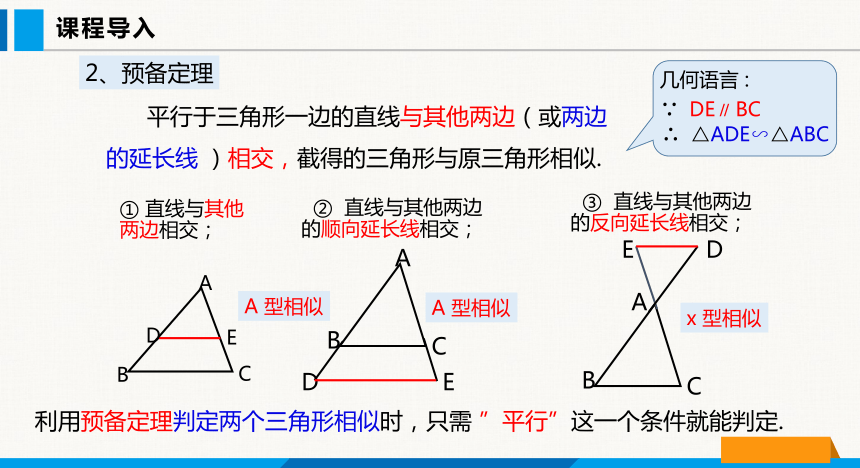
平行于三角形一边的直线与其他两边(或两边的延长线 )相交,截得的三角形与原三角形相似.
2、预备定理
A
B
C
D
E
① 直线与其他两边相交;
A
B
C
D
E
② 直线与其他两边的顺向延长线相交;
A
B
C
D
E
③ 直线与其他两边的反向延长线相交;
几何语言 :
∵ DE∥ BC
∴ △ADE∽△ABC
A 型相似
利用预备定理判定两个三角形相似时,只需 ”平行”这一个条件就能判定.
课程导入
A 型相似
根据定义,要判定两个三角形相似,必须证明对应角相等,对应边成比例(对应边长度的比相等);而根据 预备定理判定三角形相似必须要有平行线的条件,哪能都有平行线呢?
那么能不能像 判定三角形全等一样,用较少的条件就能判定三角形相似呢?
接下来,我们来研究:怎样的条件可以判定两个三角形相似.
课程导入
课程讲授
新课推进
已知:如图,在△ABC和△A'B'C'中,∠A=∠A’,∠B=∠B’.
求证:△ABC∽△A'B'C'
A
B
C
A'
B'
C'
证明:
过点D作DE∥ BC,交AC于点E,
在△ABC的边AB上,截取AD=A'B',
则 △ADE∽△ABC
∵ ∠ADE=∠B,
∴ ∠ADE=∠B’
在△ADE与△A'B'C'中
∠A=∠A’
∵
D
E
AD=A'B'
∠ADE=∠B’
∴ △ADE≌△A'B'C'(ASA)
∴ △ABC∽△A'B'C'
∠B=∠B'
,
探索1:两角分别相等的两个三角形相似
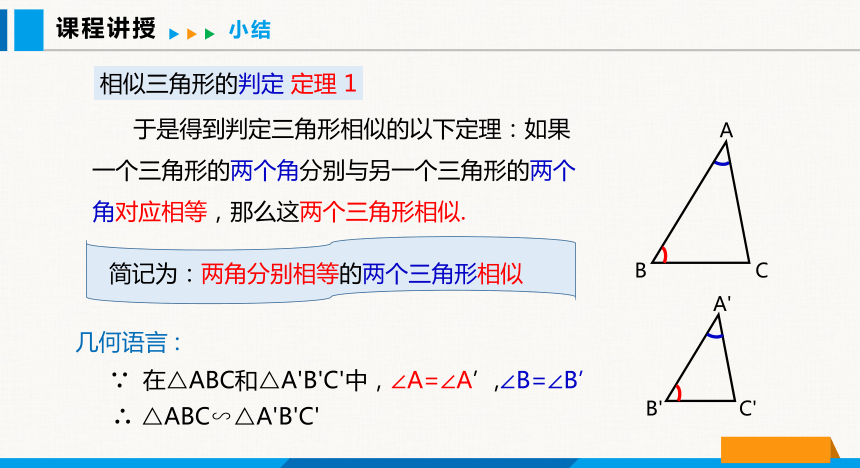
于是得到判定三角形相似的以下定理:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.
相似三角形的判定 定理 1
A
B
C
A'
B'
C'
,
简记为:两角分别相等的两个三角形相似
几何语言 :
∵ 在△ABC和△A'B'C'中,∠A=∠A’,∠B=∠B’
∴ △ABC∽△A'B'C'
小结
课程讲授
课程讲授
新课推进
如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC, AB=7,AD=5,DE=10,求BC的长.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
∴△ADE∽△ABC
(两角分别相等的两个三角形相似).
∴
∴ BC=14.
B
A
D
E
C
例1
课程讲授
新课推进
证明:
∵∠BAC= ∠1+ ∠DAC,
∠DAE= ∠3+ ∠DAC,∠1=∠3,
∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,
∠E=180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE.
如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
例2
1. 如图,已知 AB∥DE,∠AFC =∠E,则图中相
似三角形共有 ( )
A. 1对 B. 2对
C. 3对 D. 4对
C
课程讲授
新课推进
随堂小练习
课程讲授
新课推进
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
2. 如图,△ABC 的高 AD、BE 交于点 F.
求证:
D
C
A
B
E
F
习题解析
习题1
判断题:
(1) 所有的直角三角形都相似 . ( )
(2) 有一个锐角对应相等的两直角三角形相似. ( )
(3) 所有的等边三角形都相似. ( )
(4) 所有的等腰直角三角形都相似. ( )
(5) 顶角相等的两个等腰三角形相似. ( )
(6) 有一个角相等的两个等腰三角形相似. ( )
×
√
√
√
√
×
习题2
习题解析
如果 △ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,哪么△ABC与△A2B2C2有什么关系,为什么
解:
△ABC∽△A2B2C2
理由如下:
∵ △ABC∽△A1B1C1
∴ ∠A=∠A1,
∠B=∠B1
又∵ △A1B1C1∽△A2B2C2
∴ ∠A1=∠A2,
∠B1=∠B2
∴ ∠A=∠A2,
∠B=∠B2
∴ △ABC∽△A2B2C2
三角形相似具有传递性!
习题解析
习题3
如图,在△ABC中,D是AB上一点,连接CD,∠ACD=∠ABC.
(1) 求证:△ACD∽△ABC;
(2) 若AD=6,AB=10,求AC的长.
(1) 证明:
∵ ∠A=∠A,∠ACD=∠B
∴ △ACD∽△ABC
(2) 解:
∵ △ACD∽△ABC
∴
AC
AB
=
AD
AC
∴ AC2=AD·AB
∵ AD=6,AB=10
∴ AC=2
当两个三角形已具备一角对应相等的条件时,往往先找另一角对应相等.找角相等时应注意挖掘公共角、对顶角、同角的余角(补角)等隐含条件.
如图,△ABC,△DEF均为正三角形,点D,E分别在边AB,BC上,写出所有与△DEB相似的三角形: .
△ECH
、△FGH
、△ADG
习题解析
习题4
如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的的中点.
(1) 求证:AC2=AB·AD
(2) 若AD=4,AB=6,求 的值.
CF
AF
(1) 证明:
∵ AC平分∠DAB
∴ ∠DAC=∠CAB
∵ ∠ADC=∠ACB=90°
∴ △ACB∽△ADC
∴
AB
AC
=
AC
AD
∴ AC2=AB·AD
(2) 解:
∵ ∠ACB=90°,E为AB的中点
∴ CE=AE= AB=3
1
2
∴ ∠EAC=∠ECA
∵ ∠DAC=∠CAB
∴ ∠DAC=∠ECA
∴ △AFD∽△CFE
∴
CF
AF
=
CE
AD
=
3
4
习题解析
习题5
课程总结
小结
定理:两角分别相等的两个三角形相似
利用两角判定三角形相似
相似三角形的判定定理1的运用 .
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.2 相似三角形的判定
第二课时 三角形相似的判定定理1
前 言
1.理解相似三角形的定义,掌握定义中的两个条件;(重点)
2.掌握并熟练运用相似三角形的判定定理1.(难点)
A
B
C
C′
B′
A′
学习目标及重难点
课程导入
怎样判定两个三角形相似?
1、定义法:
对应角相等,对应边长度的比相等的两个三角形叫做相似三角形.
∵ ∠A=∠A',
∠B=∠B',
∠C=∠C',
AB
A'B'
=
AC
A'C'
=
BC
B'C'
几何语言 :
∴ △ABC∽△A'B'C'
反过来
∵∠A=∠A',
∠B=∠B',
∠C=∠C',
AB
A'B'
=
AC
A'C'
=
BC
B'C'
∵△ABC∽△A'B'C'
相似三角形的定义既是相似三角形的一种判定方法,又是它的一个性质.
A
B
C
A'
C'
B'
x 型相似
平行于三角形一边的直线与其他两边(或两边的延长线 )相交,截得的三角形与原三角形相似.
2、预备定理
A
B
C
D
E
① 直线与其他两边相交;
A
B
C
D
E
② 直线与其他两边的顺向延长线相交;
A
B
C
D
E
③ 直线与其他两边的反向延长线相交;
几何语言 :
∵ DE∥ BC
∴ △ADE∽△ABC
A 型相似
利用预备定理判定两个三角形相似时,只需 ”平行”这一个条件就能判定.
课程导入
A 型相似
根据定义,要判定两个三角形相似,必须证明对应角相等,对应边成比例(对应边长度的比相等);而根据 预备定理判定三角形相似必须要有平行线的条件,哪能都有平行线呢?
那么能不能像 判定三角形全等一样,用较少的条件就能判定三角形相似呢?
接下来,我们来研究:怎样的条件可以判定两个三角形相似.
课程导入
课程讲授
新课推进
已知:如图,在△ABC和△A'B'C'中,∠A=∠A’,∠B=∠B’.
求证:△ABC∽△A'B'C'
A
B
C
A'
B'
C'
证明:
过点D作DE∥ BC,交AC于点E,
在△ABC的边AB上,截取AD=A'B',
则 △ADE∽△ABC
∵ ∠ADE=∠B,
∴ ∠ADE=∠B’
在△ADE与△A'B'C'中
∠A=∠A’
∵
D
E
AD=A'B'
∠ADE=∠B’
∴ △ADE≌△A'B'C'(ASA)
∴ △ABC∽△A'B'C'
∠B=∠B'
,
探索1:两角分别相等的两个三角形相似
于是得到判定三角形相似的以下定理:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.
相似三角形的判定 定理 1
A
B
C
A'
B'
C'
,
简记为:两角分别相等的两个三角形相似
几何语言 :
∵ 在△ABC和△A'B'C'中,∠A=∠A’,∠B=∠B’
∴ △ABC∽△A'B'C'
小结
课程讲授
课程讲授
新课推进
如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC, AB=7,AD=5,DE=10,求BC的长.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
∴△ADE∽△ABC
(两角分别相等的两个三角形相似).
∴
∴ BC=14.
B
A
D
E
C
例1
课程讲授
新课推进
证明:
∵∠BAC= ∠1+ ∠DAC,
∠DAE= ∠3+ ∠DAC,∠1=∠3,
∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,
∠E=180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE.
如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
例2
1. 如图,已知 AB∥DE,∠AFC =∠E,则图中相
似三角形共有 ( )
A. 1对 B. 2对
C. 3对 D. 4对
C
课程讲授
新课推进
随堂小练习
课程讲授
新课推进
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
2. 如图,△ABC 的高 AD、BE 交于点 F.
求证:
D
C
A
B
E
F
习题解析
习题1
判断题:
(1) 所有的直角三角形都相似 . ( )
(2) 有一个锐角对应相等的两直角三角形相似. ( )
(3) 所有的等边三角形都相似. ( )
(4) 所有的等腰直角三角形都相似. ( )
(5) 顶角相等的两个等腰三角形相似. ( )
(6) 有一个角相等的两个等腰三角形相似. ( )
×
√
√
√
√
×
习题2
习题解析
如果 △ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,哪么△ABC与△A2B2C2有什么关系,为什么
解:
△ABC∽△A2B2C2
理由如下:
∵ △ABC∽△A1B1C1
∴ ∠A=∠A1,
∠B=∠B1
又∵ △A1B1C1∽△A2B2C2
∴ ∠A1=∠A2,
∠B1=∠B2
∴ ∠A=∠A2,
∠B=∠B2
∴ △ABC∽△A2B2C2
三角形相似具有传递性!
习题解析
习题3
如图,在△ABC中,D是AB上一点,连接CD,∠ACD=∠ABC.
(1) 求证:△ACD∽△ABC;
(2) 若AD=6,AB=10,求AC的长.
(1) 证明:
∵ ∠A=∠A,∠ACD=∠B
∴ △ACD∽△ABC
(2) 解:
∵ △ACD∽△ABC
∴
AC
AB
=
AD
AC
∴ AC2=AD·AB
∵ AD=6,AB=10
∴ AC=2
当两个三角形已具备一角对应相等的条件时,往往先找另一角对应相等.找角相等时应注意挖掘公共角、对顶角、同角的余角(补角)等隐含条件.
如图,△ABC,△DEF均为正三角形,点D,E分别在边AB,BC上,写出所有与△DEB相似的三角形: .
△ECH
、△FGH
、△ADG
习题解析
习题4
如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的的中点.
(1) 求证:AC2=AB·AD
(2) 若AD=4,AB=6,求 的值.
CF
AF
(1) 证明:
∵ AC平分∠DAB
∴ ∠DAC=∠CAB
∵ ∠ADC=∠ACB=90°
∴ △ACB∽△ADC
∴
AB
AC
=
AC
AD
∴ AC2=AB·AD
(2) 解:
∵ ∠ACB=90°,E为AB的中点
∴ CE=AE= AB=3
1
2
∴ ∠EAC=∠ECA
∵ ∠DAC=∠CAB
∴ ∠DAC=∠ECA
∴ △AFD∽△CFE
∴
CF
AF
=
CE
AD
=
3
4
习题解析
习题5
课程总结
小结
定理:两角分别相等的两个三角形相似
利用两角判定三角形相似
相似三角形的判定定理1的运用 .
