22.3 第2课时 相似三角形的性质定理2,3及应用 课件(共21张PPT) 2025-2026学年数学沪科版(2024)九年级上册
文档属性
| 名称 | 22.3 第2课时 相似三角形的性质定理2,3及应用 课件(共21张PPT) 2025-2026学年数学沪科版(2024)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:53:48 | ||
图片预览






文档简介
(共21张PPT)
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.3 相似三角形的性质
第二课时 相似三角形的性质定理2,3及应用
前 言
1. 掌握相似三角形的周长比等于相似比,面积比等于相似比的平方;(重点)
2. 注重周长、面积相似比的应用.(难点)
A
C
B
A1
C1
B1
学习目标及重难点
课程导入
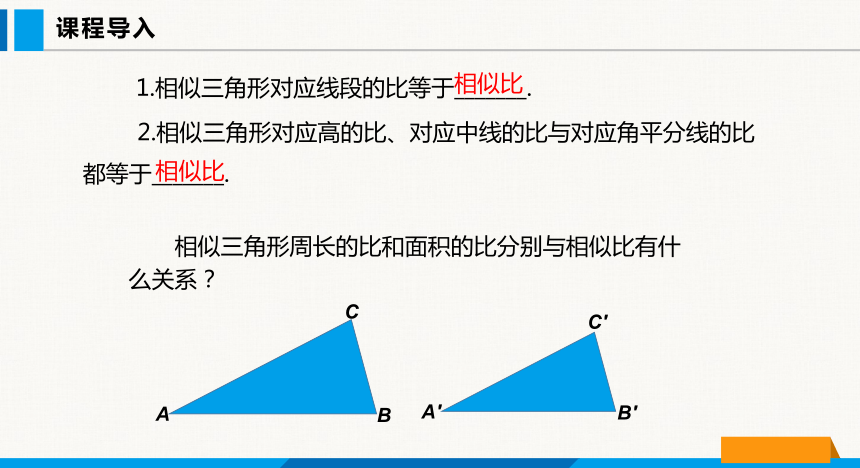
1.相似三角形对应线段的比等于_______.
2.相似三角形对应高的比、对应中线的比与对应角平分线的比都等于_______.
相似比
相似比
相似三角形周长的比和面积的比分别与相似比有什么关系?
A
B
C
C′
A′
B′
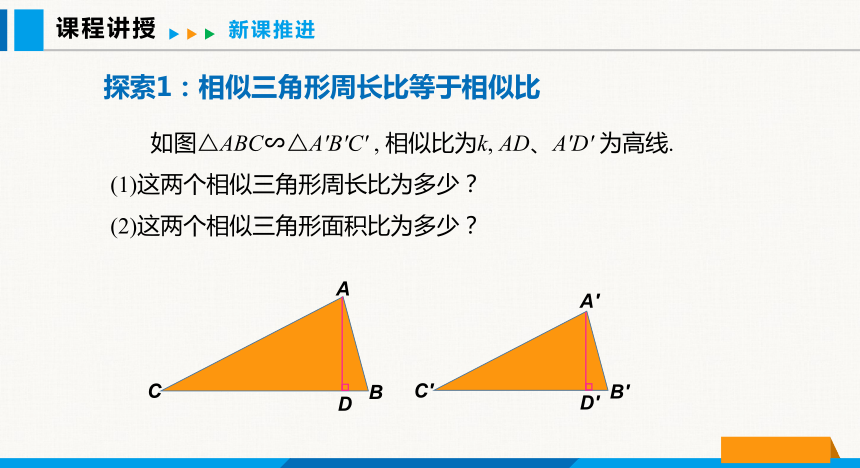
如图△ABC∽△A′B′C′ , 相似比为k, AD、A′D′ 为高线.
(1)这两个相似三角形周长比为多少?
(2)这两个相似三角形面积比为多少?
C
B
A
D
A′
C′
B′
D′
探索1:相似三角形周长比等于相似比
课程讲授
新课推进
课程讲授
新课推进
A′
C′
B′
D′
C
B
A
D
定理2 相似三角形周长的比等于相似比.
解(1)∵△ABC∽△A′B′C′ ,
∴ .
由等比性质, 得
AB
A'B'
=
AC
A'C'
=
BC
B'C'
= k
AB
A'B'
+AC
+A'C'
+BC
+B'C'
= k
课程讲授
新课推进
(2)∵△ABC∽△A′B′C′ , AD, A′D′ 是对应高.
∴ SABC =
SA′B′C′ = B′C′ A′D′
A′
C′
B′
D′
C
B
A
D
课程讲授
新课推进
定理3 相似三角形面积的比等于相似比的平方.
A′
C′
B′
D′
C
B
A
D
SABC
SA′B′C′
=
=
= k2
B′C′ A′D′
B′C′ A′D′
课程讲授
新课推进
∴ △DEF∽△ABC,相似比为
∴△DEF的周长= △ABC的周长,
△DEF的周长=12.
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,求△DEF的周长.
A
B
C
D
E
F
又 ∠D=∠A
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF
∴
例1
课程讲授
新课推进
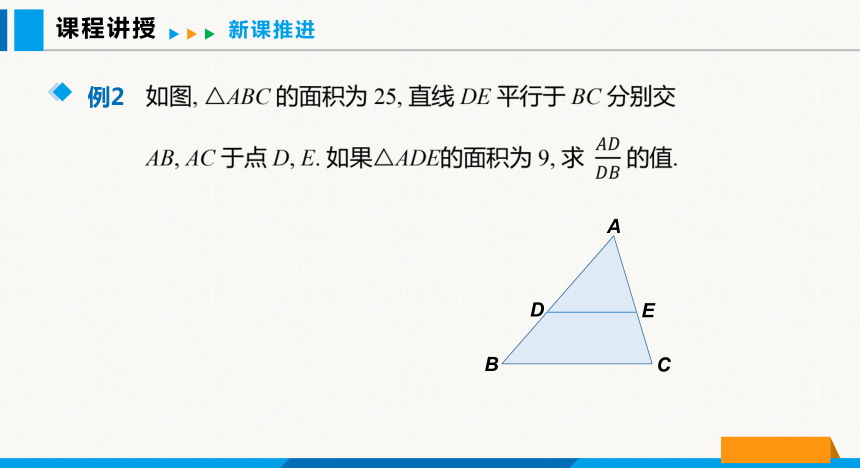
如图, △ABC 的面积为 25, 直线 DE 平行于 BC 分别交 AB, AC 于点 D, E. 如果△ADE的面积为 9, 求 的值.
A
D
B
C
E
例2
课程讲授
新课推进
A
D
B
C
E
解 ∵ DE // BC ,
∴ △ADE∽△ABC.
∴
解方程, 得
∴
.
.
课程讲授
新课推进
1.已知ΔABC与ΔA′B′C′的相似比为2:3,则对应边上中线之比 ,面积之比为 .
1:3
2:3
4:9
随堂小练习
3. 如果两个相似三角形的面积之比为 2 : 7,较大三角形一边上的高为 7,则较小三角形对应边上的高为______.
2. 如果两个相似三角形的面积之比为1:9,周长的比为______ .
习题解析
习题1
将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
即,△ABC平移的距离为
G
习题2
习题解析
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
习题解析
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
A
B
C
D
E
F
习题解析
习题3
如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求
四边形 BCDE 的面积.
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
习题解析
B
C
A
D
E
习题解析
习题4
如图,这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米, 则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,
桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,
∴△ADF ∽△ACH,
∴ 即
解得 CH = 0.9米.
∴ 阴影部分的面积为
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
习题解析
A
D
E
F
C
B
H
习题解析
习题5
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC ,
相似比为 1 : 2,
面积比为 1 : 4.
∴
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,
面积比为 1 : 4.
设 S△ABC = 4,则 S△ADE = 1,S△EFC = 1,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2,
∴ S四边形BFED : S△ABC = 2 : 4 =
习题解析
课程总结
小结
相似三角形的性质
(1)对应角相等、对应边成比例
(2)对应高之比、对应中线之比、对应角平分线之比都等于相似比
(3)周长之比等于相似比
(4)面积之比等于相似比的平方
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.3 相似三角形的性质
第二课时 相似三角形的性质定理2,3及应用
前 言
1. 掌握相似三角形的周长比等于相似比,面积比等于相似比的平方;(重点)
2. 注重周长、面积相似比的应用.(难点)
A
C
B
A1
C1
B1
学习目标及重难点
课程导入
1.相似三角形对应线段的比等于_______.
2.相似三角形对应高的比、对应中线的比与对应角平分线的比都等于_______.
相似比
相似比
相似三角形周长的比和面积的比分别与相似比有什么关系?
A
B
C
C′
A′
B′
如图△ABC∽△A′B′C′ , 相似比为k, AD、A′D′ 为高线.
(1)这两个相似三角形周长比为多少?
(2)这两个相似三角形面积比为多少?
C
B
A
D
A′
C′
B′
D′
探索1:相似三角形周长比等于相似比
课程讲授
新课推进
课程讲授
新课推进
A′
C′
B′
D′
C
B
A
D
定理2 相似三角形周长的比等于相似比.
解(1)∵△ABC∽△A′B′C′ ,
∴ .
由等比性质, 得
AB
A'B'
=
AC
A'C'
=
BC
B'C'
= k
AB
A'B'
+AC
+A'C'
+BC
+B'C'
= k
课程讲授
新课推进
(2)∵△ABC∽△A′B′C′ , AD, A′D′ 是对应高.
∴ SABC =
SA′B′C′ = B′C′ A′D′
A′
C′
B′
D′
C
B
A
D
课程讲授
新课推进
定理3 相似三角形面积的比等于相似比的平方.
A′
C′
B′
D′
C
B
A
D
SABC
SA′B′C′
=
=
= k2
B′C′ A′D′
B′C′ A′D′
课程讲授
新课推进
∴ △DEF∽△ABC,相似比为
∴△DEF的周长= △ABC的周长,
△DEF的周长=12.
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,求△DEF的周长.
A
B
C
D
E
F
又 ∠D=∠A
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF
∴
例1
课程讲授
新课推进
如图, △ABC 的面积为 25, 直线 DE 平行于 BC 分别交 AB, AC 于点 D, E. 如果△ADE的面积为 9, 求 的值.
A
D
B
C
E
例2
课程讲授
新课推进
A
D
B
C
E
解 ∵ DE // BC ,
∴ △ADE∽△ABC.
∴
解方程, 得
∴
.
.
课程讲授
新课推进
1.已知ΔABC与ΔA′B′C′的相似比为2:3,则对应边上中线之比 ,面积之比为 .
1:3
2:3
4:9
随堂小练习
3. 如果两个相似三角形的面积之比为 2 : 7,较大三角形一边上的高为 7,则较小三角形对应边上的高为______.
2. 如果两个相似三角形的面积之比为1:9,周长的比为______ .
习题解析
习题1
将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
即,△ABC平移的距离为
G
习题2
习题解析
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
习题解析
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
A
B
C
D
E
F
习题解析
习题3
如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求
四边形 BCDE 的面积.
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
习题解析
B
C
A
D
E
习题解析
习题4
如图,这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米, 则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,
桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),
DF = 1.2÷2 = 0.6 (米).
∵DF∥CH,
∴△ADF ∽△ACH,
∴ 即
解得 CH = 0.9米.
∴ 阴影部分的面积为
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
习题解析
A
D
E
F
C
B
H
习题解析
习题5
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC ,
相似比为 1 : 2,
面积比为 1 : 4.
∴
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,
面积比为 1 : 4.
设 S△ABC = 4,则 S△ADE = 1,S△EFC = 1,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2,
∴ S四边形BFED : S△ABC = 2 : 4 =
习题解析
课程总结
小结
相似三角形的性质
(1)对应角相等、对应边成比例
(2)对应高之比、对应中线之比、对应角平分线之比都等于相似比
(3)周长之比等于相似比
(4)面积之比等于相似比的平方
