22.4 第2课时 平面直角坐标系中的位似变换 课件(共26张PPT) 2025-2026学年数学沪科版(2024)九年级上册
文档属性
| 名称 | 22.4 第2课时 平面直角坐标系中的位似变换 课件(共26张PPT) 2025-2026学年数学沪科版(2024)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:55:26 | ||
图片预览


文档简介
(共26张PPT)
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.4 图形的位似变换
第二课时 平面直角坐标系中的位似变换
前 言
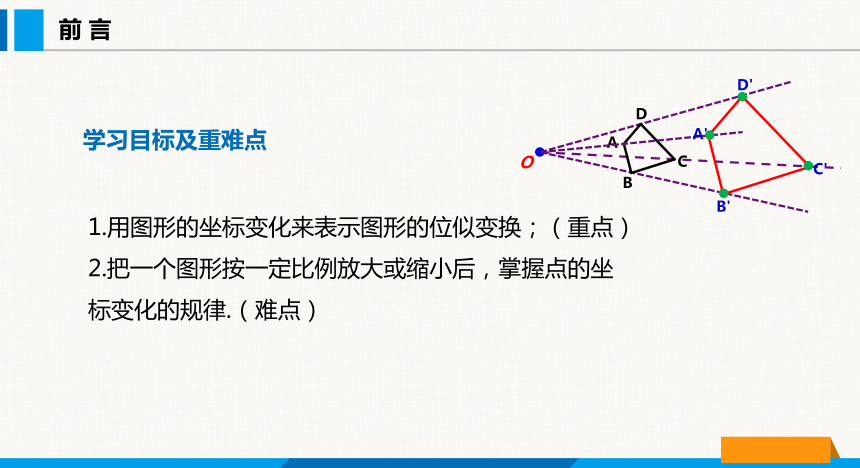
学习目标及重难点
1.用图形的坐标变化来表示图形的位似变换;(重点)
2.把一个图形按一定比例放大或缩小后,掌握点的坐标变化的规律.(难点)
A
B
C
D
A'
B'
C'
D'
O
课程导入
1. 两个相似多边形,如果它们对应顶点所在的直线相
交于一点,我们就把这样的两个图形叫做 ,
这个交点叫做 .位似图形上任意一对对应
点到位似中心的距离之比等于 ,
对应线段 .
2. 如何判断两个图形是不是位似图形
位似图形
位似中心
相似比 (或位似比)
平行或者在一条直线上
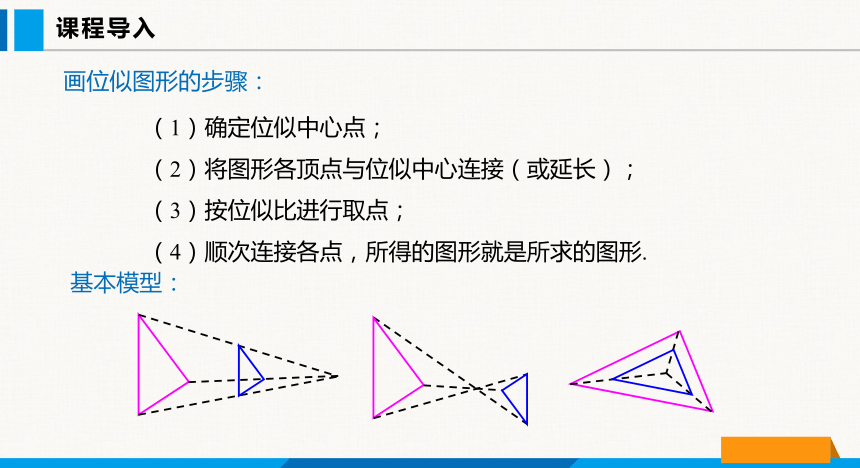
画位似图形的步骤:
(1)确定位似中心点;
(2)将图形各顶点与位似中心连接(或延长);
(3)按位似比进行取点;
(4)顺次连接各点,所得的图形就是所求的图形.
课程导入
基本模型:
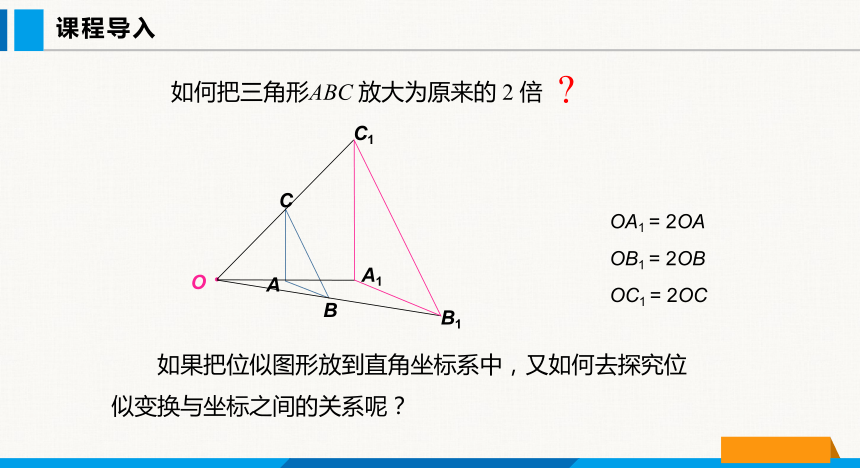
如何把三角形ABC 放大为原来的 2 倍
A
B
C
O
B1
A1
C1
OA1 = 2OA
OB1 = 2OB
OC1 = 2OC
课程导入
如果把位似图形放到直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
课程讲授
新课推进
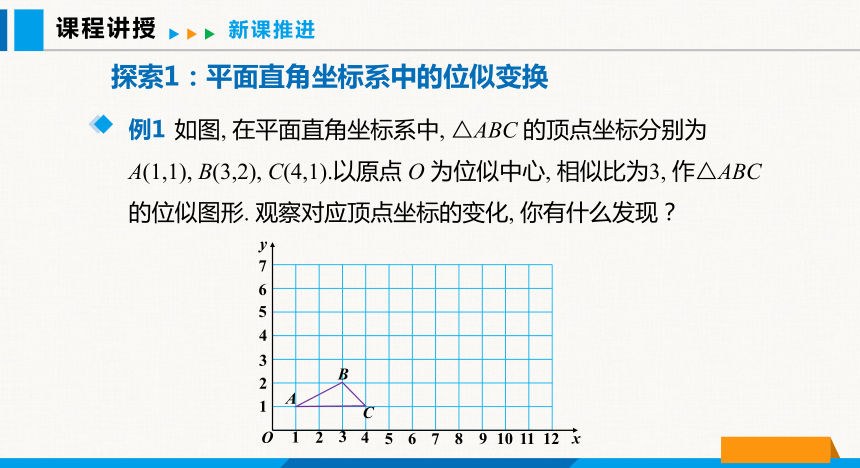
探索1:平面直角坐标系中的位似变换
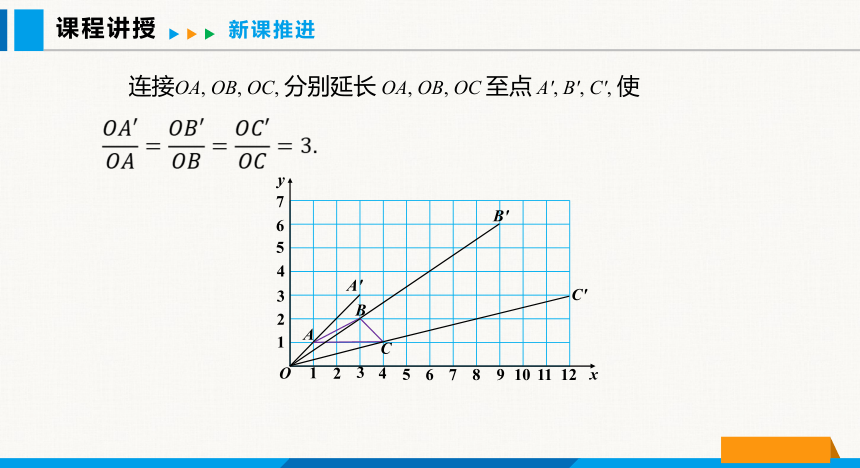
如图, 在平面直角坐标系中, △ABC 的顶点坐标分别为 A(1,1), B(3,2), C(4,1).以原点 O 为位似中心, 相似比为3, 作△ABC 的位似图形. 观察对应顶点坐标的变化, 你有什么发现?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
例1
课程讲授
新课推进
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
连接OA, OB, OC, 分别延长 OA, OB, OC 至点 A′, B′, C′, 使
课程讲授
新课推进
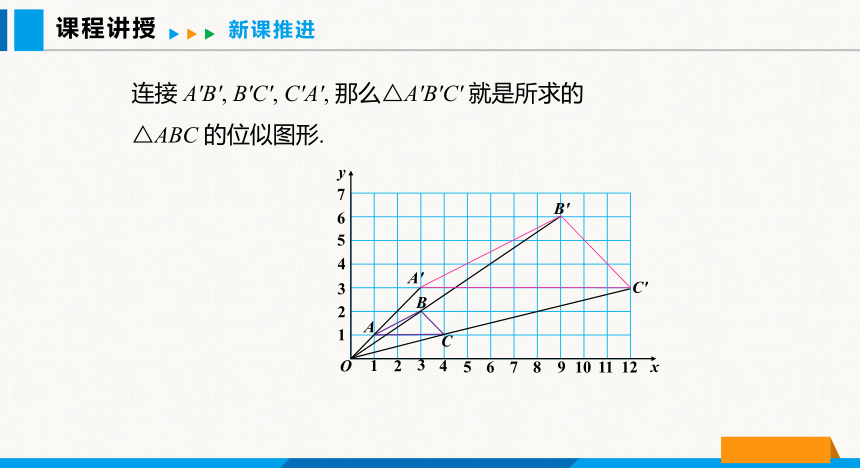
连接 A′B′, B′C′, C′A′, 那么△A′B′C′ 就是所求的△ABC 的位似图形.
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
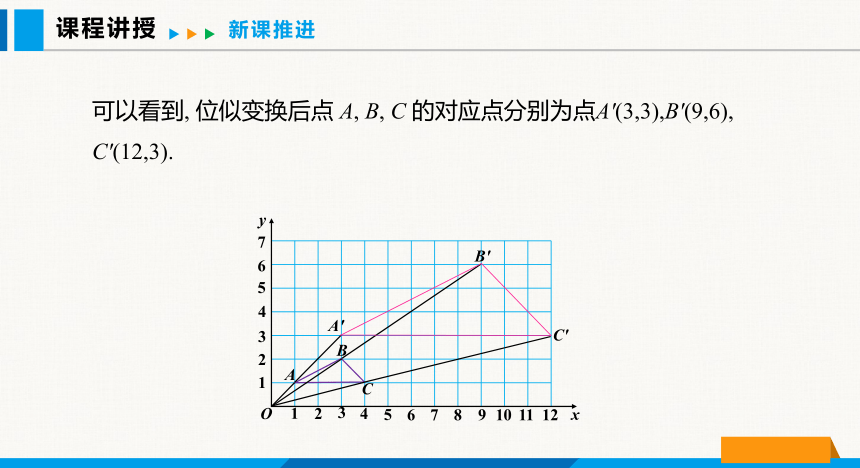
可以看到, 位似变换后点 A, B, C 的对应点分别为点A′(3,3),B′(9,6),
C′(12,3).
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
课程讲授
新课推进
课程讲授
新课推进
在平面直角坐标系中, 如果位似变换是以原点 O 为位似中心, 相似比为 k(k>0), 原图形上点的坐标为(x,y), 那么同向位似图形对应点的坐标为(kx, ky)(k>0).
利用这个性质作同向位似图形就相当简单, 只要把图形上各点的坐标都乘以一个固定的数 k(k>0), 就可以得到相似比为k(k>0)的同向位似图形.
归纳:
课程讲授
新课推进
O
x
y
A
B
C
B′
A′
C′
取 k =3, 对图中的△ABC 进行变换, 看看结果如何?
这样得到的图形叫做反向位似图形.
课程讲授
新课推进
O
x
y
A
B
C
B′
A′
C′
想一想:它与 k = 3 时的变换结果有什么不同?
课程讲授
新课推进
思考1: 将图中的△ABC, 按(x, y)→ 的方式变换, 求变换后所得图形中对应点的坐标.画出变换后图形, 它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
课程讲授
新课推进
思考2: 将图中的△ABC, 按(x, y)→(3x, y)的方式变换, 求变换后所得图形中对应点的坐标.画出变换后图形, 它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
伸缩变换
在平面直角坐标系中, 在作(x, y)→(ax, by)变换时, 当 a = b ≠ 0 时为相似变换.
课程讲授
新课推进
1. 如图,线段 AB 两个端点的坐标分别为 A (4,4),B (6,2),以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 1/2 后得到线段 CD,则端点 D 的坐标为 ( )
A. (2,2) B. (2,1)
C. (3,2) D. (3,1)
D
x
y
A
B
C
D
课程讲授
新课推进
随堂小练习
2. △ABC 三个顶点 A (3,6),B (6,2),C (2,-1),以原点为位似中心,得到的位似图形 △A′B′C′ 三个顶点分别为 A′ (1,2),B′ (2, ),C′ ( , ),则 △A′B′C′ 与 △ABC 的位似比是 .
1 : 3
课程讲授
新课推进
小结
课程讲授
1. 在平面直角坐标系中,以原点为位似中心作一个
图形的位似图形可以作两个.
2. 当位似图形在原点同侧时,其对应顶点的坐标的
比为 k;当位似图形在原点两侧时,其对应顶的
坐标的比为-k.
3. 当 k>1 时,图形扩大为原来的k 倍;当 0<k<1
时,图形缩小为原来的 k 倍.
归纳:
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在右图所示的图案中,你能找到这些变换吗
课程讲授
新课推进
习题解析
习题1
将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变
B. 将各点的横坐标除以 2,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 2,横坐标加上 2
C
习题2
习题解析
如图,小朋在坐标系中以 A 为位似中心画了两个位似的直角三角形,可不小心把 E 点弄脏了,则 E 点坐标为 ( )
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6)
A
习题解析
习题3
如图所示,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .
(-2a,-2b)
习题解析
习题4
原点 O 是 △ABC 和 △A′B′C′ 的位似中心,点 A
(1,0) 与点 A′ (-2,0) 是对应点,△ABC 的面积
是 ,则 △A′B′C′ 的面积是 .
6
习题解析
习题5
△ABC 三个顶点坐标分别为 A (2,-2),B (4,-5),C (5,-2),以原点 O 为位似中心,将这个三角形放大为原来的 2 倍.
C
2
4
6
-4
x
y
A
B
2
-2
答案:
A' (4,-4),
B' (8, -10),
C' (10,-4);
B'
A'
C'
A"
B"
C"
A″ (-4,4),
B″ (-8,10),
C″ (-10,4).
O
习题解析
在 13×13 的网格图中,已知 △ABC 和点 M (1,2).
x
y
A
B
C
(1) 以点 M 为位似中心,位似比为 2,画出 △ABC的位似图形 △A′B′C′;
M
A′
B′
C′
解:如图所示.
(2) 写出 △A′B′C′ 的各顶点坐标.
答:△A′B′C′ 的各顶点坐标分别为 A′ (3,6),B′ (5,2),C′ (11,4).
习题6
课程总结
小结
一般地, 在平面直角坐标系中, 如果以原点为位似中心, 新图形与原图形的相似比为 k, 那么与原图形上的点(x,y)对应的位似图形上的点的坐标为__________________.
(kx, ky)或(-kx, -ky)
在平面直角坐标系中在作 (x, y) (x, ay)或(ax, y)变换时, 叫伸缩变换.
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.4 图形的位似变换
第二课时 平面直角坐标系中的位似变换
前 言
学习目标及重难点
1.用图形的坐标变化来表示图形的位似变换;(重点)
2.把一个图形按一定比例放大或缩小后,掌握点的坐标变化的规律.(难点)
A
B
C
D
A'
B'
C'
D'
O
课程导入
1. 两个相似多边形,如果它们对应顶点所在的直线相
交于一点,我们就把这样的两个图形叫做 ,
这个交点叫做 .位似图形上任意一对对应
点到位似中心的距离之比等于 ,
对应线段 .
2. 如何判断两个图形是不是位似图形
位似图形
位似中心
相似比 (或位似比)
平行或者在一条直线上
画位似图形的步骤:
(1)确定位似中心点;
(2)将图形各顶点与位似中心连接(或延长);
(3)按位似比进行取点;
(4)顺次连接各点,所得的图形就是所求的图形.
课程导入
基本模型:
如何把三角形ABC 放大为原来的 2 倍
A
B
C
O
B1
A1
C1
OA1 = 2OA
OB1 = 2OB
OC1 = 2OC
课程导入
如果把位似图形放到直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
课程讲授
新课推进
探索1:平面直角坐标系中的位似变换
如图, 在平面直角坐标系中, △ABC 的顶点坐标分别为 A(1,1), B(3,2), C(4,1).以原点 O 为位似中心, 相似比为3, 作△ABC 的位似图形. 观察对应顶点坐标的变化, 你有什么发现?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
例1
课程讲授
新课推进
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
连接OA, OB, OC, 分别延长 OA, OB, OC 至点 A′, B′, C′, 使
课程讲授
新课推进
连接 A′B′, B′C′, C′A′, 那么△A′B′C′ 就是所求的△ABC 的位似图形.
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
可以看到, 位似变换后点 A, B, C 的对应点分别为点A′(3,3),B′(9,6),
C′(12,3).
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
课程讲授
新课推进
课程讲授
新课推进
在平面直角坐标系中, 如果位似变换是以原点 O 为位似中心, 相似比为 k(k>0), 原图形上点的坐标为(x,y), 那么同向位似图形对应点的坐标为(kx, ky)(k>0).
利用这个性质作同向位似图形就相当简单, 只要把图形上各点的坐标都乘以一个固定的数 k(k>0), 就可以得到相似比为k(k>0)的同向位似图形.
归纳:
课程讲授
新课推进
O
x
y
A
B
C
B′
A′
C′
取 k =3, 对图中的△ABC 进行变换, 看看结果如何?
这样得到的图形叫做反向位似图形.
课程讲授
新课推进
O
x
y
A
B
C
B′
A′
C′
想一想:它与 k = 3 时的变换结果有什么不同?
课程讲授
新课推进
思考1: 将图中的△ABC, 按(x, y)→ 的方式变换, 求变换后所得图形中对应点的坐标.画出变换后图形, 它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
课程讲授
新课推进
思考2: 将图中的△ABC, 按(x, y)→(3x, y)的方式变换, 求变换后所得图形中对应点的坐标.画出变换后图形, 它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
伸缩变换
在平面直角坐标系中, 在作(x, y)→(ax, by)变换时, 当 a = b ≠ 0 时为相似变换.
课程讲授
新课推进
1. 如图,线段 AB 两个端点的坐标分别为 A (4,4),B (6,2),以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 1/2 后得到线段 CD,则端点 D 的坐标为 ( )
A. (2,2) B. (2,1)
C. (3,2) D. (3,1)
D
x
y
A
B
C
D
课程讲授
新课推进
随堂小练习
2. △ABC 三个顶点 A (3,6),B (6,2),C (2,-1),以原点为位似中心,得到的位似图形 △A′B′C′ 三个顶点分别为 A′ (1,2),B′ (2, ),C′ ( , ),则 △A′B′C′ 与 △ABC 的位似比是 .
1 : 3
课程讲授
新课推进
小结
课程讲授
1. 在平面直角坐标系中,以原点为位似中心作一个
图形的位似图形可以作两个.
2. 当位似图形在原点同侧时,其对应顶点的坐标的
比为 k;当位似图形在原点两侧时,其对应顶的
坐标的比为-k.
3. 当 k>1 时,图形扩大为原来的k 倍;当 0<k<1
时,图形缩小为原来的 k 倍.
归纳:
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在右图所示的图案中,你能找到这些变换吗
课程讲授
新课推进
习题解析
习题1
将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变
B. 将各点的横坐标除以 2,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 2,横坐标加上 2
C
习题2
习题解析
如图,小朋在坐标系中以 A 为位似中心画了两个位似的直角三角形,可不小心把 E 点弄脏了,则 E 点坐标为 ( )
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6)
A
习题解析
习题3
如图所示,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .
(-2a,-2b)
习题解析
习题4
原点 O 是 △ABC 和 △A′B′C′ 的位似中心,点 A
(1,0) 与点 A′ (-2,0) 是对应点,△ABC 的面积
是 ,则 △A′B′C′ 的面积是 .
6
习题解析
习题5
△ABC 三个顶点坐标分别为 A (2,-2),B (4,-5),C (5,-2),以原点 O 为位似中心,将这个三角形放大为原来的 2 倍.
C
2
4
6
-4
x
y
A
B
2
-2
答案:
A' (4,-4),
B' (8, -10),
C' (10,-4);
B'
A'
C'
A"
B"
C"
A″ (-4,4),
B″ (-8,10),
C″ (-10,4).
O
习题解析
在 13×13 的网格图中,已知 △ABC 和点 M (1,2).
x
y
A
B
C
(1) 以点 M 为位似中心,位似比为 2,画出 △ABC的位似图形 △A′B′C′;
M
A′
B′
C′
解:如图所示.
(2) 写出 △A′B′C′ 的各顶点坐标.
答:△A′B′C′ 的各顶点坐标分别为 A′ (3,6),B′ (5,2),C′ (11,4).
习题6
课程总结
小结
一般地, 在平面直角坐标系中, 如果以原点为位似中心, 新图形与原图形的相似比为 k, 那么与原图形上的点(x,y)对应的位似图形上的点的坐标为__________________.
(kx, ky)或(-kx, -ky)
在平面直角坐标系中在作 (x, y) (x, ay)或(ax, y)变换时, 叫伸缩变换.
