22.5 综合与实践 测量与误差 课件(共35张PPT) 2025-2026学年数学沪科版(2024)九年级上册
文档属性
| 名称 | 22.5 综合与实践 测量与误差 课件(共35张PPT) 2025-2026学年数学沪科版(2024)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:56:15 | ||
图片预览









文档简介
(共35张PPT)
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.5 综合与实践 测量与误差
前 言
1.通过测量旗杆的高度的活动,并复习巩固相似三角形有关知识;
2.灵活运用三角形相似的知识解决实际问题.
学习目标及重难点
A
B
M
D
N
C
课程导入
怎样测量这些非常高大物体的高度?
课程导入
课程导入
我们知道, 两个三角形相似, 它们的对应角相等, 对应边成比例.
若△ABC ∽△DEF, 则有
A
B
C
D
E
F
∠A=∠D, ∠B=∠E, ∠C=∠F
在学校的操场上, 有一根不锈钢旗杆, 在既不攀爬到旗杆上, 又不破坏旗杆的情况下, 要求测量出旗杆的高度.
想一想
下面有四种测量方法,测量中可使用的工具有:皮尺、测角器、1米竿(长度为1m的竹竿)、镜子、长竿(长度大于人身高的竹竿).
课程讲授
新课推进
探索1:利用相似三角形测量高度
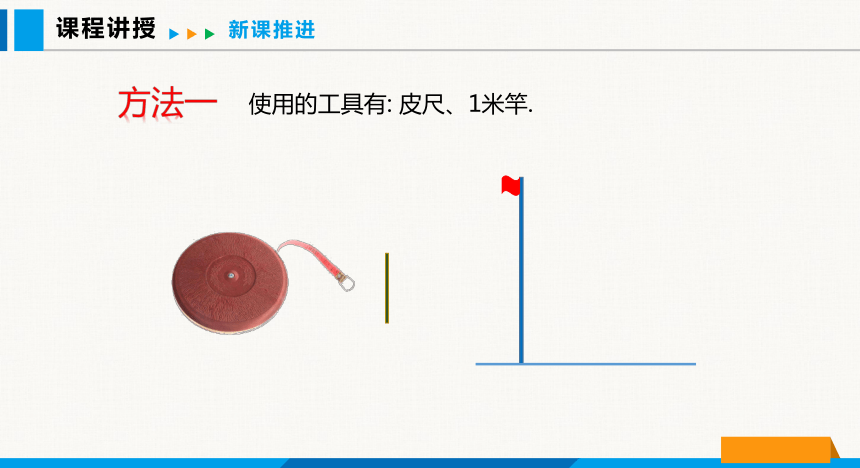
使用的工具有: 皮尺、1米竿.
课程讲授
新课推进
方法一
课程讲授
新课推进
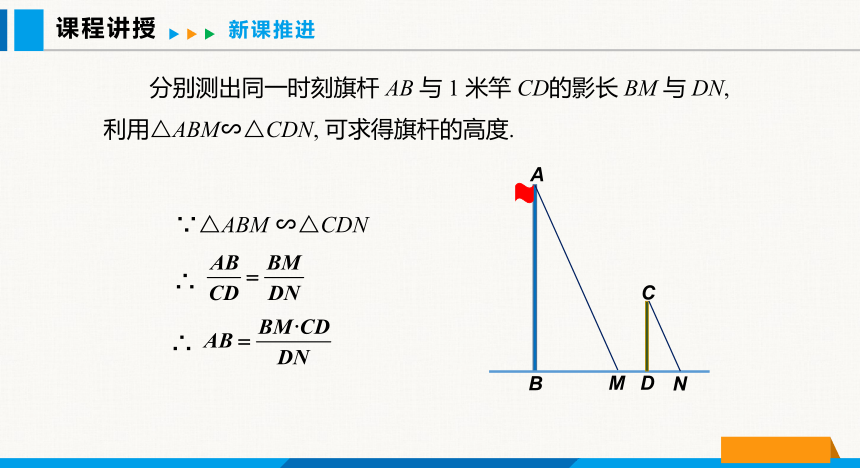
分别测出同一时刻旗杆 AB 与 1 米竿 CD的影长 BM 与 DN, 利用△ABM∽△CDN, 可求得旗杆的高度.
A
B
M
D
N
C
∵△ABM ∽△CDN
∴
∴
课程讲授
新课推进
使用的工具有: 皮尺、长竿(长度大于人身高的竹竿).
方法二
课程讲授
新课推进
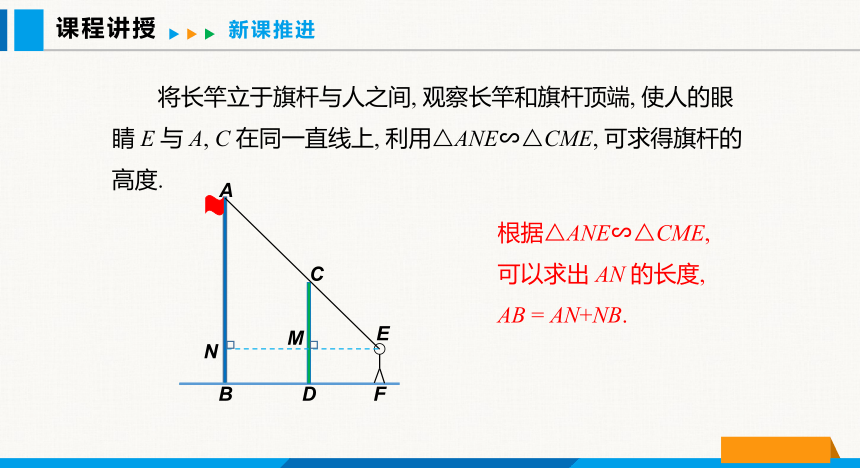
将长竿立于旗杆与人之间, 观察长竿和旗杆顶端, 使人的眼睛 E 与 A, C 在同一直线上, 利用△ANE∽△CME, 可求得旗杆的高度.
A
B
D
F
E
C
N
M
根据△ANE∽△CME,可以求出 AN 的长度,
AB = AN+NB.
使用的工具有: 皮尺、镜子.
课程讲授
新课推进
方法三
课程讲授
新课推进
A
A′
B
C
F
E
将镜面朝上置于地面 C 处, 观察镜子中旗杆顶端 A′ , 使人的眼睛 E 与 C , A′ 在同一直线上,利用△ABC≌△A′BC, △A′BC∽△EFC, 可求得旗杆的高度.
课程讲授
新课推进
使用的工具有: 皮尺、测角器.
方法四
课程讲授
新课推进
通过测角器观察旗杆顶端A, 使测角器的示数为60°(条件允许可以是45°、30°),
可求得旗杆的高度.
A
B
E
F
C
M
60°
课程讲授
新课推进
问题1: 请你用这四种方法进行旗杆测量, 并将测量数据记录于下列表格中.
测量旗杆的高度 测量次序 方法一 方法二 方法三 方法四 BM DN NM ME EF BC CF EF ME EF
1
2
3
平均值
计算结果
课程讲授
新课推进
问题2: 你觉得何种方法操作简便, 又是何种方法测得的数据更准确?你还有其他的测量方法吗?
问题3: 在测量中, 每次的测量数据都有差异, 你是如何处理的, 你测量了几次?
问题4: 几种测量方法为何有误差, 如何改进?请对测量误差进行思考, 查找误差原因.
方法一:测量不能到达顶部的物体的高度, 通常用“在同一时刻物体高与影长成正比例”的原理解决.
=
物高
杆高
物影
杆影
小结
课程讲授
测高的方法
如图,木杆 EF 长 2 m,它的影长 FD 为3m,测得 OA 为 201 m,求金字塔的高度 BO.
怎样测出
OA 的长?
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
∴ ,
∴
=134 (m).
因此金字塔的高度为134 m.
课程讲授
新课推进
例1
方法二:测量不能到达顶部的物体的高度,也可以用“利用标杆测量高度”的原理解决.
小结
课程讲授
测高的方法
如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了
课程讲授
新课推进
例2
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.
视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.
课程讲授
新课推进
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.
即
解得 EH=8.
课程讲授
新课推进
小结
课程讲授
方法三:测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
测高的方法
A
F
E
B
O
┐
┐
还可以有其他测量方法吗?
OB
EF
=
OA
AF
△ABO∽△AEF
OB =
OA · EF
AF
平面镜
想一想:
课程讲授
新课推进
为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
D
B
A
C
E
2
1
课程讲授
新课推进
例3
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,解得 BA=18.75(m).
因此,树高约为18.75m.
习题1
习题解析
1. 小明身高 1.5 米,在操场的影长为 2 米,同时测得教学大楼在操场的影长为 60 米,则教学大楼的高度应为 ( )
A. 45米 B. 40米 C. 90米 D. 80米
2. 小刚身高 1.7 m,测得他站立在阳光下的影子长为0.85 m,紧接着他把手臂竖直举起,测得影子长为 1.1 m,那么小刚举起的手臂超出头顶 ( )
A. 0.5m B. 0.55m C. 0.6m D . 2.2m
A
A
习题解析
习题2
如图是小明设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后,刚好射到古城墙的顶端 C 处,已知 AB = 2 米,且测得 BP = 3 米,DP = 12 米,那么该古城墙的高度是 ( )
A. 6米 B. 8米 C. 18米 D. 24米
B
习题解析
习题3
如图所示,有点光源 S 在平面镜上面,若在 P 点看 到点光源的反射光线,并测得 AB=10 cm,BC=20 cm,PC⊥AC,且 PC=24 cm,则点光源 S 到平面镜的距离 SA 的长度为 .
12 cm
习题解析
习题4
如图 ,利用标杆BE测量建筑物的高度。如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?
解:
∴ EB∥CD
∴△ABE∽△ACD
CD=10.5m.
∵EB⊥AC , CD⊥AC
1.2m
12.4m
1.6m
习题解析
习题解析
习题5
如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米,EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米, 到旗杆的水平距离 DC = 20 米,求旗杆的高度.
A
B
C
D
G
E
F
习题解析
A
B
C
D
G
E
F
解:由题意可得,△DEF∽△DCA,
∵DE=0.5米,EF=0.25米,DG=1.5米,DC=20米,
则
解得 AC = 10,
故 AB = AC + BC
= 10 + 1.5 = 11.5 (m).
答:旗杆的高度为 11.5 m.
∴
如图,某一时刻,旗杆 AB 的影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆 AB 在地面上的影长 BC 为 9.6 m,在墙面上的影长 CD 为 2 m.同一时刻,小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m.请帮助小明求出旗杆的高度.
A
B
C
D
习题解析
习题6
E
解:如图,过点 D 作 DE∥BC,交 AB 于点 E,
∴ DE = CB = 9.6 m,BE = CD = 2 m,
∵ 在同一时刻物高与影长成正比例,
∴ EA : ED=1 : 1.2,
∴ AE = 8 m,
∴ AB = AE + EB = 8 + 2 = 10 (m),
∴ 学校旗杆的高度为 10 m.
A
B
C
D
习题解析
课程总结
小结
利用相似三角形测高
利用阳光下的影子
利用标杆
利用镜子的反射
沪科版九年级上册 第二十二章
课程讲授
课程导入
习题解析
课堂总结
22.5 综合与实践 测量与误差
前 言
1.通过测量旗杆的高度的活动,并复习巩固相似三角形有关知识;
2.灵活运用三角形相似的知识解决实际问题.
学习目标及重难点
A
B
M
D
N
C
课程导入
怎样测量这些非常高大物体的高度?
课程导入
课程导入
我们知道, 两个三角形相似, 它们的对应角相等, 对应边成比例.
若△ABC ∽△DEF, 则有
A
B
C
D
E
F
∠A=∠D, ∠B=∠E, ∠C=∠F
在学校的操场上, 有一根不锈钢旗杆, 在既不攀爬到旗杆上, 又不破坏旗杆的情况下, 要求测量出旗杆的高度.
想一想
下面有四种测量方法,测量中可使用的工具有:皮尺、测角器、1米竿(长度为1m的竹竿)、镜子、长竿(长度大于人身高的竹竿).
课程讲授
新课推进
探索1:利用相似三角形测量高度
使用的工具有: 皮尺、1米竿.
课程讲授
新课推进
方法一
课程讲授
新课推进
分别测出同一时刻旗杆 AB 与 1 米竿 CD的影长 BM 与 DN, 利用△ABM∽△CDN, 可求得旗杆的高度.
A
B
M
D
N
C
∵△ABM ∽△CDN
∴
∴
课程讲授
新课推进
使用的工具有: 皮尺、长竿(长度大于人身高的竹竿).
方法二
课程讲授
新课推进
将长竿立于旗杆与人之间, 观察长竿和旗杆顶端, 使人的眼睛 E 与 A, C 在同一直线上, 利用△ANE∽△CME, 可求得旗杆的高度.
A
B
D
F
E
C
N
M
根据△ANE∽△CME,可以求出 AN 的长度,
AB = AN+NB.
使用的工具有: 皮尺、镜子.
课程讲授
新课推进
方法三
课程讲授
新课推进
A
A′
B
C
F
E
将镜面朝上置于地面 C 处, 观察镜子中旗杆顶端 A′ , 使人的眼睛 E 与 C , A′ 在同一直线上,利用△ABC≌△A′BC, △A′BC∽△EFC, 可求得旗杆的高度.
课程讲授
新课推进
使用的工具有: 皮尺、测角器.
方法四
课程讲授
新课推进
通过测角器观察旗杆顶端A, 使测角器的示数为60°(条件允许可以是45°、30°),
可求得旗杆的高度.
A
B
E
F
C
M
60°
课程讲授
新课推进
问题1: 请你用这四种方法进行旗杆测量, 并将测量数据记录于下列表格中.
测量旗杆的高度 测量次序 方法一 方法二 方法三 方法四 BM DN NM ME EF BC CF EF ME EF
1
2
3
平均值
计算结果
课程讲授
新课推进
问题2: 你觉得何种方法操作简便, 又是何种方法测得的数据更准确?你还有其他的测量方法吗?
问题3: 在测量中, 每次的测量数据都有差异, 你是如何处理的, 你测量了几次?
问题4: 几种测量方法为何有误差, 如何改进?请对测量误差进行思考, 查找误差原因.
方法一:测量不能到达顶部的物体的高度, 通常用“在同一时刻物体高与影长成正比例”的原理解决.
=
物高
杆高
物影
杆影
小结
课程讲授
测高的方法
如图,木杆 EF 长 2 m,它的影长 FD 为3m,测得 OA 为 201 m,求金字塔的高度 BO.
怎样测出
OA 的长?
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
∴ ,
∴
=134 (m).
因此金字塔的高度为134 m.
课程讲授
新课推进
例1
方法二:测量不能到达顶部的物体的高度,也可以用“利用标杆测量高度”的原理解决.
小结
课程讲授
测高的方法
如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了
课程讲授
新课推进
例2
分析:如图,设观察者眼睛的位置 (视点) 为点 F,画出观察者的水平视线 FG,它交 AB,CD 于点 H,K.
视线 FA,FG 的夹角 ∠AFH 是观察点 A 的仰角. 类似地,∠CFK 是观察点 C 时的仰角,由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域 (盲区) 之内. 再往前走就根本看不到 C 点了.
课程讲授
新课推进
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD.
∴△AEH∽△CEK.
即
解得 EH=8.
课程讲授
新课推进
小结
课程讲授
方法三:测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
测高的方法
A
F
E
B
O
┐
┐
还可以有其他测量方法吗?
OB
EF
=
OA
AF
△ABO∽△AEF
OB =
OA · EF
AF
平面镜
想一想:
课程讲授
新课推进
为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
D
B
A
C
E
2
1
课程讲授
新课推进
例3
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,解得 BA=18.75(m).
因此,树高约为18.75m.
习题1
习题解析
1. 小明身高 1.5 米,在操场的影长为 2 米,同时测得教学大楼在操场的影长为 60 米,则教学大楼的高度应为 ( )
A. 45米 B. 40米 C. 90米 D. 80米
2. 小刚身高 1.7 m,测得他站立在阳光下的影子长为0.85 m,紧接着他把手臂竖直举起,测得影子长为 1.1 m,那么小刚举起的手臂超出头顶 ( )
A. 0.5m B. 0.55m C. 0.6m D . 2.2m
A
A
习题解析
习题2
如图是小明设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后,刚好射到古城墙的顶端 C 处,已知 AB = 2 米,且测得 BP = 3 米,DP = 12 米,那么该古城墙的高度是 ( )
A. 6米 B. 8米 C. 18米 D. 24米
B
习题解析
习题3
如图所示,有点光源 S 在平面镜上面,若在 P 点看 到点光源的反射光线,并测得 AB=10 cm,BC=20 cm,PC⊥AC,且 PC=24 cm,则点光源 S 到平面镜的距离 SA 的长度为 .
12 cm
习题解析
习题4
如图 ,利用标杆BE测量建筑物的高度。如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?
解:
∴ EB∥CD
∴△ABE∽△ACD
CD=10.5m.
∵EB⊥AC , CD⊥AC
1.2m
12.4m
1.6m
习题解析
习题解析
习题5
如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边DE 与旗杆顶点 A 在同一直线上,已知 DE = 0.5 米,EF = 0.25 米,目测点 D 到地面的距离 DG = 1.5 米, 到旗杆的水平距离 DC = 20 米,求旗杆的高度.
A
B
C
D
G
E
F
习题解析
A
B
C
D
G
E
F
解:由题意可得,△DEF∽△DCA,
∵DE=0.5米,EF=0.25米,DG=1.5米,DC=20米,
则
解得 AC = 10,
故 AB = AC + BC
= 10 + 1.5 = 11.5 (m).
答:旗杆的高度为 11.5 m.
∴
如图,某一时刻,旗杆 AB 的影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆 AB 在地面上的影长 BC 为 9.6 m,在墙面上的影长 CD 为 2 m.同一时刻,小明又测得竖立于地面长 1 m 的标杆的影长为 1.2 m.请帮助小明求出旗杆的高度.
A
B
C
D
习题解析
习题6
E
解:如图,过点 D 作 DE∥BC,交 AB 于点 E,
∴ DE = CB = 9.6 m,BE = CD = 2 m,
∵ 在同一时刻物高与影长成正比例,
∴ EA : ED=1 : 1.2,
∴ AE = 8 m,
∴ AB = AE + EB = 8 + 2 = 10 (m),
∴ 学校旗杆的高度为 10 m.
A
B
C
D
习题解析
课程总结
小结
利用相似三角形测高
利用阳光下的影子
利用标杆
利用镜子的反射
